2

For example, the seat tube and rear axle of a bicycle or motorcycle. That is, when viewed from above, the seat tube would appear 'perpendicular' to the rear axle. But in 3d reality, the lines are skew. I was wondering if there is a single word or concise way to describe such lines.

MJD
  • 65,394
  • 39
  • 298
  • 580
Carlton Henderson
  • 23
  • 1
    There's no special name, it's just that the projections on some plane are orthogonal. – Najib Idrissi Dec 15 '14 at 17:23
  • That's not quite right, as for any two non-parallel lines there exists a plane such that the projection of the lines onto that planes are orthogonal... – user7530 Dec 15 '14 at 17:38
  • "perpendicularly skew"? "lines with orthogonal direction vectors"? I'll note that an orthocentric tetrahedron (aka, an "orthogonal tetrahedron") is defined simply as "a tetrahedron where all three pairs of opposite edges are perpendicular"; of course, those opposite edges are skew, as well, and we implicitly agree that "perpendicular" in this context describes the directions. – Blue Dec 15 '14 at 18:02

1 Answers1

1

Let $m$ and $n$ be "perpendicular but skew" lines. I suppose that you need to introduce a line parallel to $m$, call it $m_1$, such that $m_1$ and $n$ are coplanar. If $m_1$ and $n$ are coplanar they can be perpendicular to each other. So, now we have $n \perp m_1$.

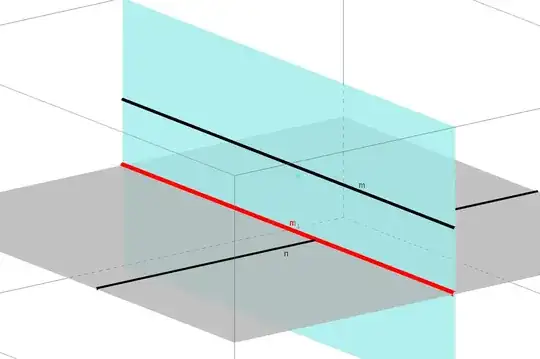
perpendicular but skew lines

So essentially $m$ is parallel to a line which is perpendicular to $n$. $m_1$ is coplanar to both $m$ and $n$. I think that Najib Idrissi's comment about orthogonal projections might help you explain the relationship by noting that if you project $m$ into a plane containing $n$ you will find $m$'s projection to be perpendicular.

EDIT: updated summary of Najib's comment.

Community
  • 1
Nick H
  • 895
  • 1
    (+1) Ok now. The critical element missing from Najib's comment is that you can only use planes parallel to one of the lines. – user7530 Dec 15 '14 at 18:33