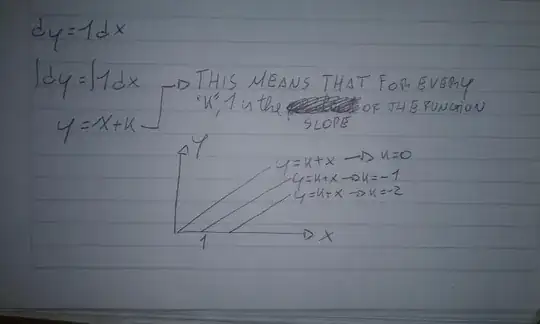Separable differential equations: detaching dy/dx

Question

I'm just learning about differential equation separability. I understand what a derivative is. One notation for derivative is $\frac{dy}{dx}$, which - misleadingly - is not a fraction. Since it's not a fraction, why are we "separating" differential equations by treating it as if it were a fraction? For example:

We have the following differential equation: $$\frac{dy}{dx} = y.$$

Then we separate the... whatever they are: $$\frac{dy}{y} = x\cdot dx.$$

What do $dy$ and $dx$ even represent when they are detached from each other? How is this valid math?

Then we integrate both sides of the equation. Even though we are integrating one side with $dy$ and the other side with $dx$, the equality is somehow magically not broken.

Also, somehow integrating $dy$ yields $y$, but integrating $dx$ doesn't yield $x$.

So my question is how do you make sense of $dy$ and $dx$ variables as they are separated from each other?

Answer 1

Treating $\frac{dy}{dx}$ like a fraction is, as you have correctly stated, not really correct. What's really going on is the following (to stay with your example): take the differential equation

$$\frac{dy}{dx}=y(x)$$

and divide both sides by $y(x)$ (this is not a trivial step - check out user21280's answer for an example what can go wrong here if you aren't careful; I won't focus on it any further here because I don't believe this to be the main thing you are enquiring about) to obtain

$$\frac{dy}{dx}\cdot\frac{1}{y(x)}= 1$$

Using the chain rule backwards, we rewrite the LHS:

$$\frac{dy}{dx}\cdot\frac{1}{y(x)}=\frac{d}{dx}\left(\ln|y(x)|\right)$$

Plugging this in, we have

$$\frac{d}{dx}\left(\ln|y(x)|\right) = 1$$

Next we integrate both sides with respect to $x$ to obtain

$$\ln|y(x)| = x + C$$

Exponentiating and absorbing the $\pm$ that reflects the absolute value into our new constant $D$, we have the familiar solution

$$y(x) = De^x$$

Whenever you are doing separation of variables, this is effectively what happens in the background. Treating $\frac{dy}{dx}$ as a fraction is a useful way to remember this method easily and is a lot easier to write down. It also yields the correct results, so people in more applied subjects like physics do it all the time, after having ideally seen what's behind it at least once.

I think you can also make $\frac{dy}{dx}$ being the ratio of two infinitesimal quantities rigorous using differential forms, but this is an area that I have not studied, so I can't help you there.

Answer 2

Most explanations of the method of separating variables do not make clear that it only works on a region where the arithmetic operations are all valid, including the division by $y$. Here is an example where the method fails to find the correct answers if you anyhow perform invalid operations. (Well what do you expect?)

Solve for $y$ as a function of a real variable $x$ given that the differential equation $\frac{dy}{dx} = 2\sqrt{y}$ holds.

Even Wolfram Alpha gets it wrong. Most students and some teachers will fail to get it right, and also fail to identify their mistake when told they are wrong, because fixing the mistake will require a proper foundation in logic.

Hint

The answer is not $y = (x+a)^2$, which you would get by the method of separating variables. What went wrong? Note that the error would still be there if you used the theorem that allows change of variables in an integral. Look carefully at each deduction step. One step cannot be justified based on any axiom. Think basic arithmetic. After you get that, you need to consider cases and use the completeness axiom for reals to extend the open intervals on which the standard solution works.

Solution sketch

The field axioms only give you a multiplicative inverse when it is not zero. Now how to solve the problem? Split into cases. Note that you need to work on intervals since having isolated points where $y$ is nonzero is useless. First prove that for any point where $y \ne 0$, there is an open interval around $x$ for which $y \ne 0$. Then we can use the completeness axiom for reals to extend the interval in both directions as far as $y \ne 0$. Now we can use any method to solve for $y$ on that interval. Note that the method of separating variables is formally invalid, so we should use the change of variables substitution. But the prerequisite for that is that $\frac{dy}{dx}$ is continuous, so we need to prove that! Well, $y$ is differentiable and hence continuous, so $2\sqrt{y}$ is continuous. So we get the solution on the extended interval, and it shows that $y$ becomes zero in exactly one direction in this example. Hence after some checking you will get either $y = 0$ or $y = \cases{ 0 & if $x \le a$ \\ (x-a)^2 & if $x > a$ }$ for some real $a$.

Alternative subproof

In fact, the substitution theorem can be completely avoided as follows. On any interval $I$ where $y \ne 0$, we have $y'^2 = 4y$, where "${}'$" denotes the derivative with respect to $x$. Thus $(y'^2)' = (4y)'$, which gives $2y'y'' = 4y'$, and hence $y'' = 2$ since $y' = 2\sqrt{y} \ne 0$. Thus $y' = 2x+c$ on $I$ for some real $c$, and hence $y = x^2+cx+d$ on $I$ for some real $d$. Note that most of the above steps are not reversible and hence we need to check all the solutions we finally obtain with the original differential equation. We would get $c^2 = 4d$. After simple manipulation we obtain the same result for $y$ on $I$ as in the other solution. The other parts of the solution still need to be there.

Bottom line

Separating variables is not so simple as you might think. Many textbooks actually teach it wrong.

Answer 3

The idea of splitting the $dy$ and the $dx$ is really just a short-cut for the following:

Starting with a separable variable DE in the form $$f(x)=g(y)\frac{dy}{dx}$$ then integrate both sides with respect to $x$, so that$$\int f(x)dx=\int g(y)\frac{dy}{dx} dx=\int g(y) dy$$

...$+c$, of course.

Answer 4

You first have to understand what a differential is. They are infinitesimal difference between successive values of a variable.

$dy=f'(x)\,dx,$ is the mathematical definition of this expression.

Of course, $f'(x)= \frac {dy}{dx}$, so you can see them as the ratio of change of y with respect of x (following the definition of a differential).

Second, integrating $dy$ yields $y+C$, and integrating $dx$ yields $x+K$, both $C$ and $K$ being constants of integration.

Hope I clarified it a bit for you

EDIT:

For the case $f'(x)=1$

This means $\frac {dy}{dx} = 1$

if you integrate both parts in $dy=1dx$ you get $y=x+k$. –

EDIT2:

Remember, the derivative of a function is the slope of the tangent line at that point, in a linear function, its the slope of the function itself.

See? for every function $y=x+k$, they all have the same slope since in a linear function, the constant denotes where the function cuts the $x$ axis, but has nothing to do with the slope of the tangent function (itself, in this case)

Answer 5

Something that I think has not been mentioned in the other answers is the fact that $dy $ and $dx $ are just notation here. And, more importantly, they are not necessary for separation of variables.

A separable equation is of the form $$\tag {*}g (y)\,y'=f (x). $$ One solves by recognizing that, if $G $ is an antiderivative for $g $ and $F $ for $f $, the above is $$G (y (x))'=F'(x), $$ and so we obtain the equality $$G (y)=F (x)+C. $$As mentioned by user21820, putting the equation in the form $(*) $ requires care about the case $g (y)=0$.

In the end, $dy/dx $ can sometimes be treated as a quotient. But there is no need to.

Answer 6

$dy/dx$ is confusing for a lot of people, because it can stand for multiple things which unintuitively are all the same. $dy/dx$ is the rate of change with $y$ in terms of $x$. It is also the most accurate tangent line between two infinitesimal elements, which is equivalent to the ratio of two infinitesimal elements.

If you accept the chain rule, then algebraically manipulating differentials should seem more natural, they become multiplicative. At least to some degree, $dy/dx$ does represent a fraction, though you probably don't think of it that way.

If you're not comfortable with using seperable DEs, they are really just a special case for linear DEs, which don't use the seperable method. So your problem should remedy itself soon.

Answer 7

I'm going to avoid the discussion of what $dx$ and $dy$ mean, since others have provided very good answers to that, and instead clarify the specific example in the OP:

We have the following differential equation: $$\frac{dy}{dx} = y.$$

Then we separate the... whatever they are: $$\frac{dy}{y} = x\cdot dx.$$

[....] Also, somehow integrating $dy$ yields $y$, but integrating $dx$ doesn't yield $x$.

The way you've narrated the example makes me suspect that there are a few procedural things going on that you are missing, quite apart from the (very reasonable) question about what the heck any of this means. For starters, you've made a simple algebraic mistake in separating the variables. Your second equation should be $$\frac{dy}{y} = dx$$

(Note that in the OP there was an extra $x$ on the right-hand side.)

Now the sentence "integrating $dy$ yields $y$, but integrating $dx$ doesn't yield $x$" does not really match what's going on. We're not integrating $dy$, we're integrating $\frac{dy}{y}$, so the integral on the left-hand side isn't $y$, but $\ln|y|$. Meanwhile the integral of the right-hand side is $x$. Include an undetermined constant and you've got the equation $$\ln|y| = x + C$$ Exponentiating both sides gives $$|y| = e^C e^x$$ or equivalently $$|y| = Ke^x$$ where $K = e^C$ is an arbitrary positive constant. Finally we drop the absolute value signs, which we compensate for by letting the constant be either positive or negative: $$y=Ae^x$$ where $A$ is any nonzero constant.