For an app, I want to equally distribute a certain number of points on the perimeter of a known ellipse, and, to draw them, I need to know, for every point, the angle of the line that connects it to the center of the ellipse.
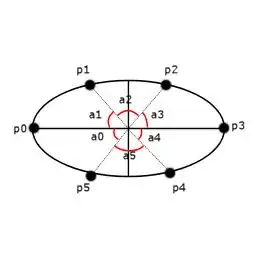
Here is an horrible drawing of what I must achieve: number of the points is known, distance of the points on the ellipse is constant (or at least should be) but unknown (well, it is circumference/number of points), horizontal and vertical radiuses are known, I look for the angles a0-an
I already know that this is a not easy problem, that does not have a finite solution. The fact is that I don't need perfection in the points distribution, but I need speed in the calculation of the positioning.
Is there a way or an easy formula that approximates the real solution? Some altorithm that makes it possible to be implemented?
Thank you in advance.