$x(t)= a\cos(t)$ , $y(t)= b\sin(t)$ in terms of the arc length $S$

Question

I'm trying to parameterize the ellipse $x(t)= a\cos(t)$ , $y(t)= b\sin(t)$ in terms of the arc length $S$ but I don't know how to do it.

Supposing that $\gamma:[a,b]\to \mathbb{R}$ is a smooth curve with $\gamma'(t)\neq 0$ for $t\in [a,b]$ , I know that $s(t)$= $\int_{a}^{t}\left\| \gamma'(\psi)\right\|d\psi$ for $t\in [a,b]$ then I find the inverse funtion of $s$.

Can anybody help me find a way to express the parameterization for the ellipse? I’m looking for a solution in terms of sine amplitude and cosine amplitude.

Answer 1

Precisely the the theory of Elliptic integrals was developed to calculate this arc length. There are no closed form for this arc length in terms of elementary functions, we need especial functions.

Recall the coordinates at any point on the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \tag{1} $$

Parametrically:

$$ x = a\sin^2 \varphi, \quad y = b\cos^2\varphi$$

Hence

$$ \sin^2 \varphi + \cos^2 \varphi = 1$$

Hence if $s$ is the perimeter of the ellipse, and if $b^2 = a^2(1-e^2)$ where $e$ is the eccentricity

Then

$$s = 4\int_{0}^{\frac{\pi}{2}} \sqrt{a^2\cos^2\varphi + b^2\sin^2 \varphi}d\varphi = 4a \underbrace{\int_{0}^{\frac{\pi}{2}}\sqrt{1-e^2\sin^2\varphi}d\varphi}_{E}$$

The integral $E$ is an especial function called the complete elliptic integral of the second kind:

$$ E(k) = \int_{0}^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2\theta}d\theta$$

where $k$ is called the modulus

Therefore

$$ s = 4aE(e)$$

The values of $E(k)$ can be calculated numerically or from tables

For example,

$$e = 0 \Longrightarrow E(e) = \frac{\pi}{2}, \quad s = 2\pi a$$ $$e = \frac{1}{2} \Longrightarrow E(e) = 1.467..., \quad s= 5.87a$$

Update:

Following suggestions of other readers we add more theory:

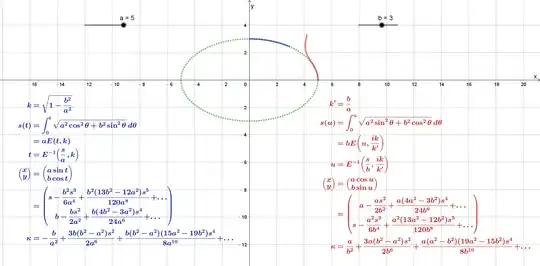
One way of writing the coordinates of any point of the ellipse (1) in parametric form is

$$ x = a\operatorname{sn} u\; \quad y = b\operatorname{cn} u $$

where $\operatorname{sn}$ and $\operatorname{cn}$ are the Jacobi theta functions which have the following relations

$$ u = F(k,\phi) = \int_{0}^{\phi} \frac{1}{\sqrt{1-k^2\sin^2 \theta}} d\theta $$

$$E(u) = E(k,\theta) = \int_{0}^{\phi} \sqrt{1-k^2\sin^2 \theta}$$

$0<k<1, \quad k'= \sqrt{1-k^2}$ are called the modulus and the complementary modulus

where this integrals are the incomplete Elliptic integral of the first and second kind, respectively

$\phi = \operatorname{am} u$ is called the amplitude

$\sin \phi = \sin(\operatorname{am} u) = \operatorname{sn} u $ is called sine-amplitude

$\cos \phi = \cos(\operatorname{am} u) = \operatorname{cn} u$ is called cosine-amplitude

$\Delta\phi =\operatorname{dn}u = \sqrt{1-k^2\sin^2 \phi}$ is called delta-amplitude

Can be proven geometrically that if $B=(0,b^2)$ and $P=(x,y)$ is a point in the ellipse with $x>0,y>0$ the arc-lenght $s$ from $B$ to $P$ is given by:

$$s = a\int_{0}^{u} \sqrt{\operatorname{cn}^2u\operatorname{dn}^2u + k'^2\operatorname{sn}^2 u \operatorname{dn}^2u} du = a\int_{0}^{u} \sqrt{\operatorname{cn}^2u\operatorname{dn}^2u + k'^2\operatorname{sn}^2 u \operatorname{dn}^2u} du = a\int_{0}^{u} \operatorname{dn}u \sqrt{\operatorname{cn}^2 u +k'^2\operatorname{sn}^2u} du = a\int_{0}^{u}\operatorname{dn}^2 u du = a\int_{0}^{\phi} \sqrt{1-e^2\sin^2 \theta}d\theta $$

Now we have all the ingredients to find $s$ the arc-lenght and to find the amplitude $\phi$ in terms of the inverse of the Jacobi theta functions

A nice reference for this is Elliptic functions with applications by Bowman.

Answer 2

As already given in comments and answers, $$s = a\int_{0}^{\phi} \sqrt{1-e^2\sin^2 (\theta)}\,\,d\theta=a E\left(\phi \left|e^2\right.\right)$$

Using series expansion $$E\left(\phi \left|e^2\right.\right)=\phi-e^2\sum_{n=1}^\infty \frac{P_n(e)}{(2n+1)!}\phi^{2n+1}$$ with $$\left( \begin{array}{cc} n & P_n(e) \\ 1 & 1 \\ 2 & 3 e^2-4 \\ 3 & 45 e^4-60 e^2+16 \\ 4 & 1575 e^6-2520 e^4+1008 e^2-64 \\ 5 & 99225 e^8-189000 e^6+105840 e^4-16320 e^2+256 \\ 6 & 9823275 e^{10}-21829500 e^8+15800400 e^6-4055040 e^4+261888 e^2-1024 \end{array} \right)$$

In order to see how good or bad is the series expansion, was computed the norm $$\Phi_n=\int_0^1 \int_0^{\frac \pi 2} \Big[E\left(\phi \left|e^2\right.\right)- \text{Series}_n\Big]^2\,d\phi\,de$$ $$\left( \begin{array}{cc} n & \Phi_n \\ 1 & 7.8491 \times 10^{-4} \\ 2 & 8.7292 \times 10^{-6} \\ 3 & 1.9078 \times 10^{-6} \\ 4 & 4.4468 \times 10^{-7} \\ 5 & 1.3816 \times 10^{-7} \\ 6 & 5.1692 \times 10^{-8} \end{array} \right)$$ So, a quite limited number of terms could be used for the inversion.

Now, using reversion of the above series (with $\color{red} {y=\frac s a}$) $$\color{red}{\phi_*=y+e^2\sum_{n=1}^\infty \frac{Q_n(e)}{(2n+1)!}y^{2n+1}}$$ with $$\left( \begin{array}{cc} n & Q_n(e) \\ 1 & 1 \\ 2 & 13 e^2-4 \\ 3 & 493 e^4-284 e^2+16 \\ 4 & 37369 e^6-31224 e^4+4944 e^2-64 \\ 5 & 4732249 e^8-5165224 e^6+1406832 e^4-81088 e^2+256 \\ 6 & 901188997 e^{10}-1212651548 e^8+474297712 e^6-56084992 e^4+1306880 e^2-1024 \end{array} \right)$$

Truncating to $n=3$, notice that $$E\left(\phi_* \left|e^2\right.\right)-y=\frac{e^2 \left(-37369 e^6+31224 e^4-4944 e^2+64\right) }{362880}y^9+O\left(y^{11}\right)$$

If you prefer a more compact expression $$\phi_*=y\, \frac {1+\frac{12-29 e^2 } {60} y^2 }{1+\frac{4-13 e^2}{20} y^2 }+O\left(y^7\right)$$ $$E\left(\phi_* \left|e^2\right.\right)-y=\frac{e^2 \left(-1381 e^4+656 e^2+176\right) }{50400}y^7+O\left(y^{9}\right)$$

Answer 3

There is no standard closed form but series solutions only

• Local canonical form starting from minor axis (clockwise convention):

\begin{align} k &= \sqrt{1-\frac{b^2}{a^2}} \\ s(t) &= \int_0^t \sqrt{a^2\cos^2 \theta+b^2\sin^2 \theta} \, d\theta \\ &= aE(t,k) \\ t &= E^{-1} \left( \frac{s}{a},k \right) \\ \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} a\sin t \\ b\cos t \end{pmatrix} \\ &= \begin{pmatrix} s-\frac{b^2 s^3}{6a^4}+\frac{b^2(13b^2-12a^2)s^5}{120a^8}+\ldots \\ b-\frac{b s^2}{2a^2}+\frac{b(4b^2-3a^2)s^4}{24a^6}+\ldots \end{pmatrix} \\ \kappa &= -\frac{b}{a^2}+\frac{3b(b^2-a^2)s^2}{2a^6}+ \frac{b(b^2-a^2)(15a^2-19b^2)s^4}{8a^{10}}+\ldots \\ \end{align}

• Local canonical form starting from major axis (anti-clockwise convention):

\begin{align} k' &= \frac{b}{a} \\ s(u) &= \int_0^u \sqrt{a^2\sin^2 \theta+b^2\cos^2 \theta} \, d\theta \\ &= bE\left( u,\frac{ik}{k'} \right) \\ u &= E^{-1}\left( \frac{s}{b},\frac{ik}{k'} \right) \\ \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} a\cos u \\ b\sin u \end{pmatrix} \\ &= \begin{pmatrix} a-\frac{a s^2}{2b^2}+\frac{a(4a^2-3b^2)s^4}{24b^6}+\ldots\\ s-\frac{a^2 s^3}{6b^4}+\frac{a^2(13a^2-12b^2)s^5}{120b^8}+\ldots \end{pmatrix} \\ \kappa &= \frac{a}{b^2}+\frac{3a(b^2-a^2)s^2}{2b^6}+ \frac{a(a^2-b^2)(19a^2-15b^2)s^4}{8b^{10}}+\ldots \\ \end{align}

• Plots of the partial sums for $s\in [0,3]$:

• Fourier series for eccentric angle:

\begin{align} ds &= a\sqrt{1-k^2\sin^2 t} \, dt \\ t &= \frac{1}{2aE(k)} \sum_{n=1}^{\infty} \sin \frac{n\pi s}{2aE(k)} \int_{-2aE}^{2aE} E^{-1} \left( \frac{s'}{a}, k \right) \sin \frac{n\pi s'}{2aE(k)} ds' \\ &= \sum_{n=1}^{\infty} \sin \frac{n\pi s}{2aE(k)} \int_{-\pi}^{\pi} \underbrace{ \frac{\tau \sqrt{1-k^2\sin^2 \tau}}{2E(k)} \sin \frac{n\pi E(\tau,k)}{2E(k)} }_{\text{expand as Maclaurin series in }k} \, d\tau \\ &= \frac{\pi s}{2aE(k)}- \left( \frac{k^2}{8}+\frac{k^4}{16}+\ldots \right) \sin \frac{\pi s}{aE(k)}+\left( \frac{5k^4}{256}+\ldots \right) \sin \frac{2\pi s}{aE(k)}-\ldots \\ \end{align}

• The first term comes from sawtooth waveform:

$$\frac{\pi s}{2aE(k)}=\phi=2 \left( \sin \phi-\frac{\sin 2\phi}{2}+\frac{\sin 3\phi}{3}-\ldots \right)$$

• Compare with the Jacobi amplitude here.

• See also the anti-clockwise version in my older post here.

Answer 4

Intrinsic differential equation of all Conics ( semi-latus rectum $p$, primed on arc ) was found by differentiation of Newton's form of Conics in the form:

$$x'= \cos \phi; \;y'=\sin \phi; \;p \phi' = \sin^3 (\phi-\tan^{-1}\frac{y}{x}). $$

Could be solved in terms of incomplete Elliptic functions.

I had derived this ode earlier on this site and and also sci.math ;