Using the notation $[a_0,a_1,a_2,...]$ for the continued fraction
$$ a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{...}}} $$
where $a_0 ∈ \mathbb Z$ and $a_i ∈ \mathbb N$ for all $i>0$
Question: Consider the continued fraction expansion $$ [1,0,1,1,2,1,1,4,1,1,6,1,...,1,2n,1,...] $$
and let $p_i$ and $q_i$ denote the numerators and denominators (respectively) of its convergents. Prove that
$$ p_{3n} = p_{3n-1} + p_{3n-2}, q_{3n} = q_{3n-1}+q_{3n-2} $$ $$ p_{3n+1} = 2np_{3n} + p_{3n−1}, q_{3n+1} = 2nq_{3n} +q_{3n−1} $$ $$ p_{3n+2} = p_{3n+1} + p_{3n}, q_{3n+2} = q_{3n+1} +q_{3n} $$
for $n=1,2,....$
As I understand it, the numerators are $[1,0,1,1,2,1,1,4,1,1,6,1,...,1,2n,1,...]$ while the denominator's are $[1,1,...]$. But I do not know what exactly is meant with "of its convergence".
I am also uncertain how to proceed with proving the above mentioned questions, but I do believe it relates to the "fundamental recurrence formulas" as I read a bit about in the following wikipedia article: https://en.wikipedia.org/wiki/Generalized_continued_fraction
Merry Christmas and happy new year.
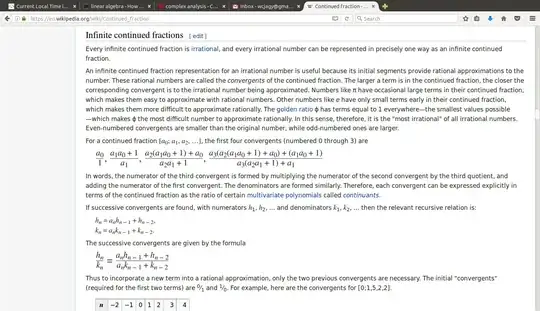
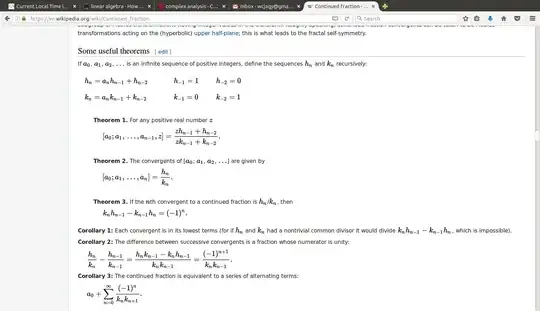
I still need to understand exactly how to apply these and where they ordinate from, but do you think I understand the assignment correctly, by saying this is what i need to understand and apply?
– Sirmimer Dec 28 '16 at 16:11