Must the surfaces embedded in $\mathbb{R}^3$ with constant Gaussian curvature be (a part of) surfaces of revolution? It seems that on the text book, the examples are only those surfaces of revolution if one talks about constant Gaussian curvature. Any counter-examples or proof? Thanks.
-
A related question – J. M. ain't a mathematician Dec 28 '16 at 15:50
-
– Narasimham Jan 12 '17 at 14:19
1 Answers
Every "generalized cylinder" or "generalized cone" has Gaussian curvature identically zero. Most of these are not surfaces of rotation.
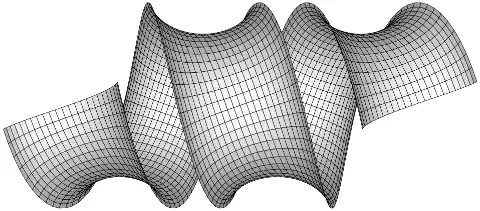
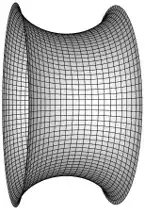
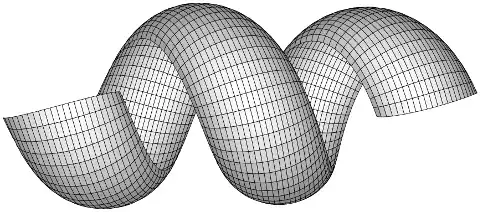
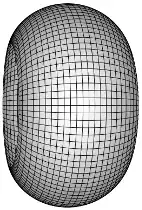
More interestingly, for each surface of rotation having constant Gaussian curvature, there is a one-parameter family of "helical" surfaces of constant Gaussian curvature, the parameter being the "pitch" of the helix. (The family arising this way from the pseudosphere is Dini's surface.)
There are also surfaces of constant negative Gaussian curvature having no ambient symmetries. This is physically clear if you imagine a hyperbolic patch made from a sheet of rubber or paper: The patch is "floppy", and most of its physical configurations cannot be "slid along themselves".
Edit: Parametric formulas for helical surfaces of constant curvature (joint work with J. M. Antonio, 2008, unpublished) are given in terms of differential equations, just as for surfaces of rotation.
Fix real numbers $k$, $C > 0$, and $B > 0$, and let $$ G(u) = \begin{cases} \phantom{\pm} B^{2} - u^{2} & K = 1, \\ \phantom{\pm} B^{2} + C^{2}u & K = 0, \\ \pm B^{2} + u^{2} & K = -1. \end{cases} $$ If we define \begin{align*} h_{2}(u) &= \sqrt{G(u) - k^{2}}, \\ h_{1}'(u) &= \sqrt{\frac{G(u)}{G(u) - k^{2}} \left[\frac{1}{G(u)} - \frac{G'(u)^{2}}{4(G(u) - k^{2})}\right]}, \\ \psi'(u) &= -\frac{k}{G(u)}\, h_{1}'(u), \end{align*} then $$ \mathbf{x}(u, v) = \left[ \begin{array}{@{}c@{}} h_{1}(u) + k(v + \psi(u)) \\ h_{2}(u) \cos(v + \psi(u)) \\ h_{2}(u) \sin(v + \psi(u)) \\ \end{array}\right] $$ parametrizes a helical surface of constant Gaussian curvature in each interval where $$ 0 < G(u) - k^{2}\quad\text{and}\quad \frac{G(G')^{2}}{4(G - k^{2})} \leq 1. $$ The surface is immersed, but not necessarily embedded, and is not geodesically complete unless $k = 0$ and $G(u) = 1 - u^{2}$ (the sphere), or $C = 0$ in the flat case (a cylinder). Taking $B = 0$ in the negative-curvature case gives helical surfaces converging to the pseudosphere as $k \to 0$.
- 78,195
-
Hi, very nice. Curvature lines are in red I suppose... Is it mentioned in book Modern Diff.Geom Curves/ Surfaces by Alfred Gray BTW? Wish you showed the hypo variety also alongwith. Cannot find it in Wiki either ! I mention it as OP ( as had also much earlier) considered this was missing from the DG literature. An addition of twisted positive curvature surfaces would be great.. – Narasimham Dec 28 '16 at 16:04
-
@Narasimham: Yes, the grid lines are lines of curvature. (Had to re-generate images, hence the grayscale. In addition to Dini's surface, there are two families where the profile hits the axis.) I don't know if the surface of rotation examples are in Gray's book, but the profile curves are fairly standard material. In Barrett O'Neill's Elementary DIfferential Geometry, revised second edition, they can be found on pages 259 and 261. Formulas at Revolution surfaces of constant Gaussian curvature. – Andrew D. Hwang Dec 28 '16 at 17:52
-
(K<0) In catenoid- helicoid deformation (surface of revolution-spiral ) we have curvature lines getting converted to asymptotics and vice-versa.Does a similar thing happen here also? (through k-factor). I never saw any image of full deformation where the central parallels map to a middle straight line. Could one see this image? – Narasimham Jan 06 '17 at 20:41
-
In these examples, varying $k$ maps lines of curvature to lines of curvature (i.e., the coordinate grids get "carried along with the surface"), since the metric turns out to have the form $(1/G(u)), du^{2} + G(u), dv^{2}$ independently of $k$ (so the given parametrizations represent local isometries) and the lines of curvature are coordinate curves (which are clearly preserved by varying $k$). When you ask about the "full deformation", do you mean the catenoid-helicoid deformation? – Andrew D. Hwang Jan 06 '17 at 22:18
-
Thanks. I learn this from you, Yes I meant the same cat-hel deformation which you simulated above. – Narasimham Jan 06 '17 at 22:34
-
Can you please indicate, if curvature and torsion of extreme ( base/central) helices are $ a/(a^2+b^2)$ and $b/(a^2+b^2), $ then what are the parametric representation of these two type of surfaces? – Narasimham Jan 29 '17 at 05:59
-
@Narasimham The parametrizations are set up so that $u = 0$ is the central helix, and the "edge" helices (for non-zero curvature) occur where$$\frac{G(G')^{2}}{4(G - k^{2})} = 1,$$which (in principle, by solving an ODE) allows the curvature and torsion to be computed in terms of $u$ and $G$. (It's safe to assume $\psi = 0$ for these purposes.) Does that address your question? – Andrew D. Hwang Jan 29 '17 at 15:53
-
Hope one of these days you would post an animation of these unwinding spirals, $K>0, K<0$ We are more familiar with catenoid/helicoid animations. – Narasimham Jan 30 '17 at 19:32
-
Andrew D Hwang: As helical surfaces can we expect geodesic torsion or geodesic curvature to be constant, or be any functions of parameter $u$? – Narasimham Jun 26 '17 at 12:06
-
@Narasimham: You mean the curvature and torsion of geodesics through a point? Offhand I don't know, but I'd expect "any ("sufficiently reasonable") functions of $u$". – Andrew D. Hwang Jun 26 '17 at 17:30
-
No, I mean on the surface $x(u,v).$ Only already defined parametric lines $ u=const, v=const , $ evaluation of. properties $\tau_{g}(u,v), \kappa_{g}(u,v). $ – Narasimham Jun 26 '17 at 20:45