I recently asked a question about how to find value of $\sin(\pi/18)$ and I understand that there is no expression for $\sin(\pi/18)$ that uses the ordinary arithmetical operations. but I know that we have exact value by nested radicals. I want to know how we get this value ?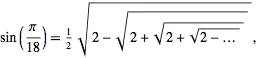
- 4,379
-
1Essentially, such a nested radical is the solution to a certain polynomial equation. You can identify this equation for a given nested radical by just attempting to do operations to it until you get the same value. In this case it looks like the radical (without the factor of $1/2$) can be obtained from itself by performing the operation "square both sides and then subtract 2" three times. Thus it satisfies $x=((x^2-2)^2-2)^2-2$, which is a certain polynomial equation, which you could hope to derive by trigonometric principles. – Ian Nov 05 '16 at 23:52
-
Of course what I've explained is really reverse engineering this formula, not finding it in the first place, but it is a start. – Ian Nov 05 '16 at 23:53
-
Yes , you are right. It is reverse engineering but I want to know how we get this equation. Thank you – S.H.W Nov 06 '16 at 00:00
-
1As for how to come up with it in the first place, the point is that you are trisecting $\pi/6$. Thus consider $\sin(3x)=Im((\cos(x)+i\sin(x))^3)=Im(\cos(x)^3+3i\cos(x)^2\sin(x)-3\cos(x)\sin(x)^2-i\sin(x)^3)=3\cos(x)^2 \sin(x)-\sin(x)^3=(3-3\sin(x)^2)\sin(x)-\sin(x)^3=3\sin(x)-4\sin(x)^3$. So with $x=\pi/18$ you have the equation $1/2=3\sin(\pi/18)-4\sin(\pi/18)^3$. This can actually be solved in radicals using the cubic formula. It won't give you such a nested radical, though (that would have to be induced by a sixth degree polynomial). – Ian Nov 06 '16 at 00:03
-
see also (http://mathworld.wolfram.com/NestedRadical.html) – Jean Marie Nov 06 '16 at 00:05
-
@lan As I write , there is no expression for sin(π/18) that uses the ordinary arithmetical operations and you can't solve that cubic equation – S.H.W Nov 06 '16 at 00:21
-
@S.H.W I've provided a theorem in my answer. And also an alternative method for finding the convergence... – Frank Nov 06 '16 at 00:22
-
Yes , It's Wonderful ! Thanks a lot. – S.H.W Nov 06 '16 at 00:23
-
@Frank How we can prove this convergence ? – S.H.W Nov 06 '16 at 00:31
-
@S.H.W Show that $a_{6n+1}>a_{6n+2}> a_{6n+3}> a_{6n+4}$ and $a_{6n+4}<a_{6n+5}<a_{6n+6}<a_{6n+7}$ – Frank Nov 06 '16 at 00:45
-
And how we can calculate formula that is in Theorem ? – S.H.W Nov 06 '16 at 01:07
-
@S.H.W See my new edit! – Frank Nov 06 '16 at 18:19
2 Answers
Theorem 1: For $a_1=\sqrt a$, $a_2=\sqrt{a-\sqrt{a}}, a_3=\sqrt{a-\sqrt{a+\sqrt a}},\ldots,$ We have $a_n$ as$$\lim_{n\rightarrow\infty}a_n=\frac {A-1}6+\frac 23\sqrt{4a+A}\sin\left(\frac 13\arctan\frac {2A+1}{3\sqrt3}\right)\tag1$$where $A=\sqrt{4a-7}$.
Proof: I present to you the proof for the theorem.
Start with $$x^2=y+a,\qquad y^2=z+a\qquad z^2=x+a\tag{2.1}$$
Then we can factor the resulting $8$ degree polynomial into factors $$x^3+\frac 12x^2\left\{1+\sqrt{4a-7}\right\}-\frac 12x\left\{2a+1-\sqrt{4a-7}\right\}+\frac 12\left\{a-2-a\sqrt{4a-7}\right\}\tag{2.2}$$ and $$x^3+\frac 12x^2\left\{1-\sqrt{4a-7}\right\}-\frac 12x\left\{2a+1+\sqrt{4a-7}\right\}+\frac 12\left\{a-2+a\sqrt{4a-7}\right\}\tag{2.3}$$. For brevity, we can let $A=\sqrt{4a-7}$ and use the identity$$\sin^3\theta-\frac 34\sin\theta+\frac 14\sin3\theta=0$$
We first consider $(2.2)$. Substituting $x=s-\frac {A+1}{6}$ and recalling that $A^2=4a-7$, we find that$$s^3+\left(\frac {A-4a}3\right)s+\frac {12a-14-A-8Aa}{27}=0\tag{2.4}$$
And similarly, setting $x=s-\frac {1-A}6$ in $(2.3)$, we get$$s^3+\left(\frac {-A-4a}3\right)s+\frac {12a-14+A+8Aa}{27}=0\tag{2.5}$$ Which we notice is the same as $(2.4)$, but with $A$ replaced with $-A$. Next, setting $s=\frac 23t\sqrt{4a-A}$ and $s=\frac 23t\sqrt{4a+A}$ in $(2.4)$ and $(2.5)$ respectively, we deduce$$\begin{align*} & t^3-\frac 34t+\frac {12a-14-A-8Aa}{8(4a-A)^{3/2}}=0\\ & t^3-\frac 34t+\frac {12a-14+A+8Aa}{8(4a+A)^{3/2}}=0\end{align*}\tag{2.6}$$ Setting $t=\sin\theta$ and using the identity, we get the solutions to $(2.6)$. Simplifying and more simplifying, we get Theorem 1.
Simply plugging in $a=2$ gives you $2\sin\frac {\pi}{18}$ and dividing both sides by two, you get your first equation.$$\frac 12\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2-\ldots}}}}=\sin\frac {\pi}{18}\tag3$$
- 5,984
-
-
1@Ian Sure. http://www.maa.org/sites/default/files/images/upload_library/22/Ford/Berndt-Bhargava644-656.pdf – Frank Nov 06 '16 at 00:14
-
-
-
@Frank I don't how we can change the variable ? For example how you substituted $x$ and $s$ ? – S.H.W Mar 11 '17 at 10:44
-
@Frank Thank you a lot for your answers . I want to know how did you find these changing variables ? In the other words how you got $x=s-\frac {1-A}6$ and $s=\frac 23t\sqrt{4a-A}$ ? – S.H.W Mar 12 '17 at 08:26
-
@Frank Okay , Thank you . It's too weird honestly how he could get that . – S.H.W Jun 23 '17 at 00:41
-
@S.H.W Well, Ramanujan substituted $x$ with $s-(1-A)/6$ solely to get rid of the $x^2$ term (a common way to solve the general cubic), and then Ramanujan probably substituted $s$ with the expression to get the coefficient of $s$ down to a rational number. Of course, how he managed to see $s=\tfrac 23t\sqrt{4a-A}$ is a mystery. – Crescendo Jul 19 '17 at 19:34
Deriving $\sin\frac{\pi}{18}$ will be simpler when we implement Half angle cosine formula $$2\sin\frac{\theta}{2} = \sqrt{2-2\cos\theta}$$ $$2\cos\frac{\theta}{2} = \sqrt{2+2\cos\theta}$$
and cosine angle identity
$$2\cos(\pi-\theta) = -2\cos\theta$$
We can derive as follows $2\sin(\frac{\pi}{18})$ = $\sqrt{2-2\cos(\frac{\pi}{9})}$ = $\sqrt{2-\sqrt{2+2\cos(\frac{2\pi}{9}})}$ = $\sqrt{2-\sqrt{2+\sqrt{2+2\cos(\frac{4\pi}{9}}})}$ = $\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+2\cos(\frac{8\pi}{9}}}})}$ = $\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2-2\cos(\frac{\pi}{9}}}})}$
Now you can observe $2\cos(\frac{\pi}{9})$ repeats in cycle infinitely
$$\therefore 2\sin\frac{\pi}{18} = \sqrt{2-\sqrt{2+\sqrt{2+...}}}$$ $[-++]$ is the repeating pattern in infinite nested radical. Refer here. Welcome to the world of infinite nested square roots of 2 as solution to cosine angles!
- 1,017