0

I know that statement is right in many examples but when I wanted to find exact value of $10$ degree , I achieved this equation : $8t^3 - 6t + 1 = 0$ where $t = \sin10$ . Also I know we have a nested radical expression for it (See :http://mathworld.wolfram.com/TrigonometryAnglesPi18.html ) And contradiction appears when it's a root of equation and we can also solve it by Cardano's method and this gives us a closed formula for $\sin 10$.

S.H.W
  • 4,379
  • 1
    What is the question? – Simply Beautiful Art Mar 05 '17 at 19:55
  • Where is the contradiction? – Berci Mar 05 '17 at 19:56
  • @SimplyBeautifulArt I want to know how it is possible that a root of cubic equation be infinity nested radical. – S.H.W Mar 05 '17 at 20:21
  • @SimplyBeautifulArt And also how we can get this nested radical solution from $8t^3 - 6t + 1 = 0$ equation ? – S.H.W Mar 05 '17 at 20:23
  • SHW why are you talking about nested radicals? Do you have an explicit example of that? There are some questions on this site that used such things; but, they are less general than one might expect. – Will Jagy Mar 05 '17 at 20:27
  • take a look at this item by Tito: http://math.stackexchange.com/questions/1065862/something-strange-about-sqrt-4-sqrt-4-sqrt-4-x-x-and-its-friends – Will Jagy Mar 05 '17 at 20:31
  • You seem to talk about the constructibility with ruler and compass. Square-roots can be constructed this way, but not irrational cubic-roots. There is no possibility to construct $\sin(10°)$ with ruler and compass because the minimal polynomial has degree $3$. So, there is no contradiction to the solveability by Cardanos formula (which always works, but requires ugly roots of complex numbers in the case of $3$ real numbers) – Peter Mar 05 '17 at 20:40
  • @WillJagy My problem is how solving $8t^3 - 6t + 1 = 0$ leads us to that nested radical in (http://mathworld.wolfram.com/TrigonometryAnglesPi18.html ) ? – S.H.W Mar 05 '17 at 20:41
  • @Peter This is good point thank you but my problem isn't this. – S.H.W Mar 05 '17 at 20:43
  • @Peter This is my problem : How solving $8t^3 - 6t + 1 = 0$ can leads us to that nested radical in (http://mathworld.wolfram.com/TrigonometryAnglesPi18.html ) ? – S.H.W Mar 05 '17 at 20:46
  • 1
    @Peter Is my question clear now ? – S.H.W Mar 05 '17 at 20:50
  • @S.H.W OK, I understand. These formulas give a way to construct $\sin(10^°)$, but with infinite many steps. Maybe, you can get some fix-point property by only considerting three nested square-roots. I am not sure, but a similar approach allows to calculate easier nested square-roots, but I have nothing concrete. – Peter Mar 05 '17 at 20:50
  • @Peter Okay , Previously I asked it but really didn't understand how it's related to that equation . (http://math.stackexchange.com/questions/2001269/value-of-sin-pi-18-by-nested-radicals) – S.H.W Mar 05 '17 at 20:53
  • shw I have it.... typing answer with pictures – Will Jagy Mar 05 '17 at 20:55
  • @WillJagy Okay , Thank you a lot. – S.H.W Mar 05 '17 at 20:56
  • 1
    @Peter posted an answer. The important point is not the infinite nesting, it is the recurrence, where the variable I called $x$ appears both on the left hand side of the equation and inside the radicals on the right hand side. Put another way, we have a fixpoint of a real function. – Will Jagy Mar 05 '17 at 21:13
  • 1
    @WillJagy Nice! – Peter Mar 05 '17 at 21:15
  • It is quite easy to get the value of $2\sin\frac{\pi}{18}$ as follows. Refer here and also for $2\cos\frac{\pi}{18}$. But my attempt to solve $2\cos\frac{\pi}{18}$ as $\frac{\sqrt3}{6}\cdot(\sqrt{8-\sqrt{8-\sqrt{8+...}}}+1)$ is not successful currently – Sivakumar Krishnamoorthi Jan 22 '21 at 21:44

2 Answers2

1

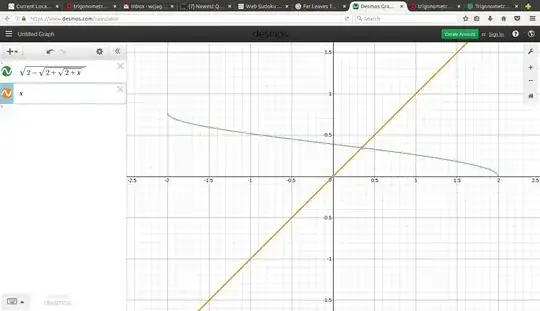
Taking $$ x = 2 \sin \left( \frac{\pi}{18} \right) \approx 0.347296 > \frac{1}{3} $$ we are told $$ x = \sqrt{2 - \sqrt{2 + \sqrt{2 + x} }}. $$ Put another way, we are demanding a fixpoint of the real valued function $$ f(w) = \sqrt{2 - \sqrt{2 + \sqrt{2 + w} }}. $$

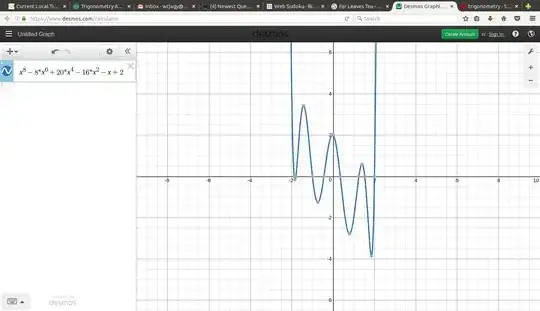
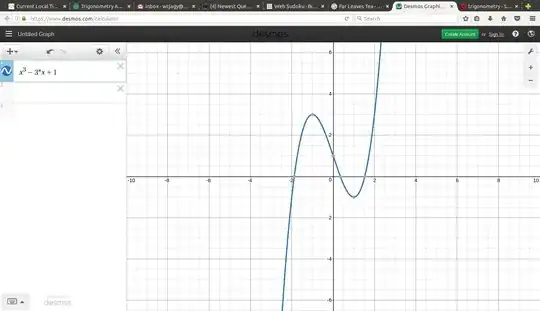
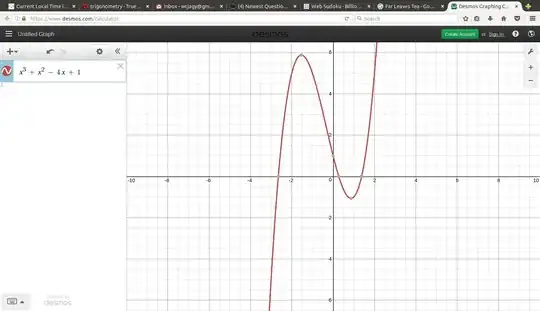
I repeatedly squared and put the polynomial terms on one side, which led to $$ x^8 - 8 x^6 + 20 x^4 - 16 x^2 - x + 2 = 0. $$ This factors, $$ \left(x-2 \right) \left( x+1 \right) \left(x^3 + x^2 - 2x+1 \right) \left( x^3 - 3x + 1\right) $$ You can see from the graphs that $x \approx 0.347$ can only be a root of the final cubic, $x^3 - 3x + 1.$ Call your quantity $s$ so that $x = 2s,$ we get $8 s^3 - 6 s + 1 = 0.$

enter image description here enter image description here enter image description here

Notice that, while the octic polynomial has eight real roots, the original function has just a single real fixpoint. enter image description here

Will Jagy
  • 139,541
  • Oh , Very good answer . Now I solved equation with Wolfram and it gives a complicated answer. Do you know an easy expression for $\sin 10$ ? – S.H.W Mar 05 '17 at 21:20
  • @S.H.W easy, no. There is Cardano's formula, as Peter mentioned. If you ever study Galois theory, you will begin to understand. As Peter also said, your $\sin 10^\circ$ falls under https://en.wikipedia.org/wiki/Casus_irreducibilis – Will Jagy Mar 05 '17 at 21:29
0

Here's a good one. Find the roots of $$ x^3 + x^2 - 4 x + 1. $$ Very trigonometric.

enter image description here

Will Jagy
  • 139,541
  • Can you explain more about your answer ? – S.H.W Mar 05 '17 at 20:22
  • 1
    @S.H.W just a good example, with quite pretty outcome. I still have no idea what your question is. Since this has three real irrational roots, it falls under https://en.wikipedia.org/wiki/Casus_irreducibilis However, very nice answer if we include trigonometric functions. – Will Jagy Mar 05 '17 at 20:26