5

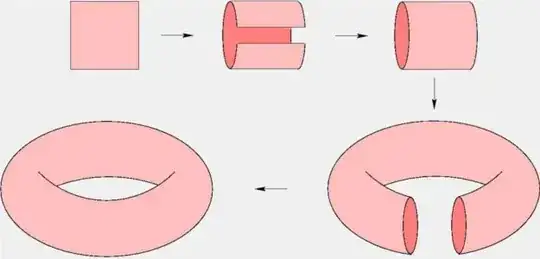
We know that torus can be obtained from a square by joining the opposite sides.

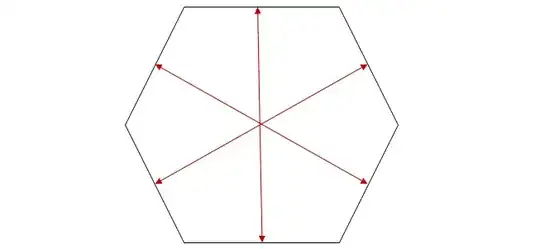
enter image description here

Can we do the same thing with a hexagon?

enter image description here

If it's not possible to 'fold' hexagon in 3D Euclidean space, may be it's possible in highter dimensions?

Of course, like in the example with a square, stretching is allowed.

I intentionaly don't use the correct topology terms, since I don't know topology. I probably should've used terms such as manifold and homeomorphism.

I hope the question is clear enough in layman terms.

Related question: What are all topological spaces obtained by gluing the edges of a triangle?

Edit

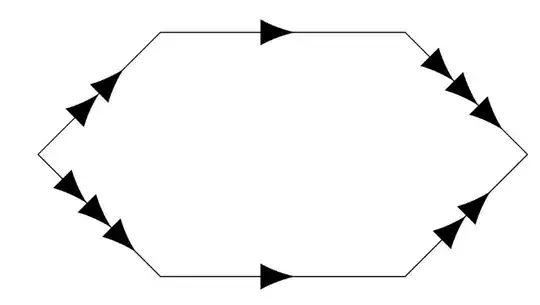
A useful link from Fredrik Meyer which probably answers the question. And the image from the link which should help with orienation:

enter image description here

we see that the surface is the torus.

Says the link. If it's true, can we show how folding a hexagon results in a torus?

Community
  • 1
Yuriy S
  • 31,474
  • 1
    How are you orienting the pairs of edges for the join? The result would be different depending on those choices. (E.g., should the top edge going left-to-right be identified with the bottom edge left-to-right, or with the bottom edge right-to-left? And then the same question for the other pairs of edges.) – Mark Dickinson Oct 21 '16 at 13:36
  • @MarkDickinson, I thought the picture was clear enough. The arrows show which sides should be joined. – Yuriy S Oct 21 '16 at 13:37
  • 3
    See this link. – Fredrik Meyer Oct 21 '16 at 13:39
  • @MarkDickinson, now I get it. They shouldn't be reflected. For example, the square above could be folded into a Mobius strip instead of torus. I mean nice bending without twist – Yuriy S Oct 21 '16 at 13:39
  • @FredrikMeyer, thanks. The link says it's the torus again, but I don't see how it could be obtained – Yuriy S Oct 21 '16 at 13:49
  • The Euler characteristic is a toplogical invariant, meaning that is does not vary with homeomorphism. What basically you are asking is, what surfaces are homeomorphic to the space containing the hexagon. The answer is the torus since $\chi(S)=0$. –  Oct 21 '16 at 14:12
  • @Bacon, thanks. Now I understand. – Yuriy S Oct 21 '16 at 16:09

1 Answers1

7

You can show it is a torus by cut and paste methods. These are the same methods used in the proof of the classification of surfaces in the comment of @Bacon, however you do not need to cite the classification of surfaces. Instead you can show by hand that this is a torus, which will have the side benefit of teaching you a little about how the classification of surfaces is proved. Roughly speaking that proof is an algorithmic process which let's you take any polygon gluing diagram and cut and paste it to put it into a normal form which let's you recognize the surface.

To do the cut and paste, first number the vertices in your hexagon picture in clockwise order as $1,2,3,4,5,6$ where $1$ is the rightmost vertex. Cut the hexagon along the line segment from vertex 3 to vertex 5, thus cutting off a triangle (the left portion) and a pentagon (the right portion). Label the two cut edges with a quadruple arrow so as to remember how to repaste them at a later time. But do not repaste them yet! Instead, paste the triple arrow edge of the triangle to the triple arrow edge of the pentagon. You now have a different gluing pattern on a hexagon. You should be able to see how this different hexagon gluing pattern is the same as an ordinary square gluing pattern, hence you get the torus.

Lee Mosher
  • 120,280