0

I'm currently self-studying Lee's text An Introduction to Topological Manifolds. I was enjoying the text up to but excluding the section on Quotient Spaces in Chapter 3, where I hit a wall. I am having a very difficult time visualizing Lee's examples of quotient spaces. In particular, I can't figure out why the figures (Fig. - 3.8, 3.9) correspond to his Examples - 3.48 and 3.49.

The examples are here:

Lee - Examples - 3.48 & 3.49

And, the corresponding figures are here:

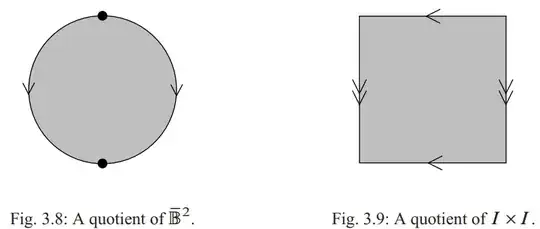
Lee - Figures - 3.8 & 3.9

My questions:

  • How does Fig. - 3.8 relate to $\mathbb{\overline{B}}^2/\sim$ ? Also, what really happens to the points in $\operatorname{Int} \mathbb{\overline{B}}^2$ ?
  • Similarly, how is Fig. - 3.9 a figure of a surface obtained by pasting the top boundary segment of the square to the bottom to form a cylinder, and then pasting the left-hand boundary circle of the resulting cylinder to the right-hand one?
math-physicist
  • 979
  • these figures indicate how to glue according to the equivalence relation. Aligned Similar arrows mean we glue along the arrows and similar arrows with different orientation mean we twist the figure so the arrows align and then glue. – LBE May 23 '23 at 04:55

1 Answers1

1

The line segments with the same arrows are to be identified in the direction of the arrows. For example, in fig 3.9, the top and bottom edges are being identified, because they are both marked by the single arrowhead. If you were just given the figures then one way of making this rigorous is to choose parametrizations of both segments consistent with the arrowheads, say the top edge as $t \mapsto (1-t, 1)$ and the bottom edge as $t \mapsto (1-t, 0)$. Now identifying these two segments means to identify $(1-t, 1) \sim (1-t, 0)$ for each $t$, or equivalently $(x, 0) \sim (x, 1)$ for each $x$. If one of the arrows was flipped then the identification would be $(1-t, 1) \sim (t, 0)$.

Implicit in this description is that the resulting quotient only depends on the "orientation" of the parametrization and not the parametrization itself (ie I could parametrize the top edge as $(1-t^3, 1)$ and the quotient I would get would be homeomorphic). In the examples here you actually start with the parametrizations and the figure is inferred so this point is not so relevant.

Since there are no markings on the interior of either figure, by default there are no added identifications on points in the interior, which is consistent with the identifications described. Of course $\sim$ should be an equivalence relation, in particular reflexive, so $p \sim p$ for every point $p$.

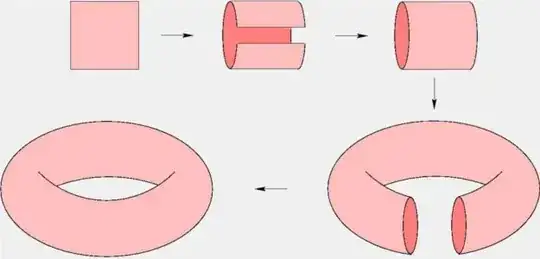
For the intuitive description of the identification, there is again the implicit fact that performing these identifications in two steps, first the horizontal edges and then the vertical edges ultimately produces the same quotient. To see that identifying the top and bottom edges produces a cylinder, you can imagine the square is a piece of paper, or if that still does not help, try to perform the identification on an actual piece of paper (square or rectangle, should not matter for this step). If you take two parallel edges of the square, and glue/tape them while matching the arrows, you get a cylinder. The remaining two edges of the square become the two circular edges of the cylinder. If the square is made of (unstretchable) paper then you can't actually glue these edges without introducing folds but if you now imagine the cylinder is stretchable, then you can "bend" it and glue the two circles together. If you keep track of the other double-headed arrows and match them up you should get a cylinder. Here is a picture of the process (taken from the related but more complicated question What surface do we get by joining the opposite edges of a hexagon?):

gluing the edges of a square into a cylinder

ronno
  • 11,390
  • This is was just the kind of explanation I was looking for. Thanks a lot for this answer. Also, perhaps you meant "$(x,0)\sim(x,1)$" instead of "$(x,1)\sim(x,1)$" ? Otherwise it's a perfect answer to my question! I wish I had these level of intuitions about quotient spaces. Is there any particular resources you know of that develops intuition about quotient spaces? Or, perhaps a software like Mathematica or something? – math-physicist May 23 '23 at 12:00
  • @math-physicist yes, thanks for catching the typo. – ronno May 23 '23 at 12:00
  • 1
    @math-physicist Unfortunately I don't know a good resource for this. Most of my own intuition is developed by understanding these basic examples of low genus surfaces, some standard constructions like suspensions and mapping tori, and a few examples of the fact that identifying a contractible subspace to a point is a homotopy equivalence (and sometimes a homeomorphism), which is more useful once you want to identify spaces up to homotopy equivalence, often in algebraic topology. – ronno May 23 '23 at 12:15
  • 1
    @math-physicist By the way if you want to visualize why fig 3.8 gives you a sphere, think of how some dumplings, like gyozas and momos, are constructed. – ronno May 23 '23 at 12:15