Tilings of the plane and quotient spaces

Question

A square lattice has two discrete translation symmetries, isormorphic to $\mathbb{Z}^2$. If we take the quotient of the plane by this group, $\mathbb{R}^2/\mathbb{Z}^2$, we get the square with opposite sides identified, which is the torus.

Can a similar argument be developed for a regular hexagonal lattice? I mean, the square has two independent translational symmetries; so does the hexagon; what is the difference, topologically? To put it differently, the hexagon with opposite sides identifies can be seen as the plane "quotiented" by some equivalence relation. But can it be seen as the quotient of two groups? Or at least two spaces?

Same as above but for equilateral triangle lattice.

Also, the symmetry group of the square lattice is bigger than just translations, it has rotations and reflections. Can we consider a different quotient in which in the numerator $\mathbb{R}^2$ is replaced by the whole 2D Euclidian group, and in the denominator $\mathbb{Z}^2$ is replaced by the whole symmmetry group of the square lattice? What do we get?

Where can I read an accessible introduction to these themes?

Answer 1

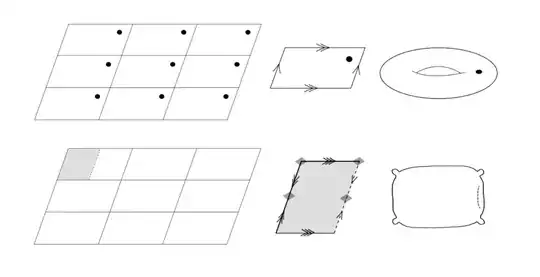
the hexagon with opposite sides identifies can be seen as the plane "quotiented" by some equivalence relation. But can it be seen as the quotient of two groups?

Yes. Let $H$ be a subgroup of $\Bbb R^2$ consisting of elements $x$ such that a translation of $\Bbb R^2$ by $x$ keeps a given regular hexagonal lattice. The group $H$ is generated by three translations by one cell, whose sum is the identity map. That is, in fact, $H$ is generated by any two of these translations and $H$ is isomorphic to $\Bbb Z^2$. A quotient topological group $\Bbb R^2/H$ is homeomorphic to a hexagonal cell of the lattice with the opposite sides identified, that is a torus again.

Can we consider a different quotient in which in the numerator $\Bbb R^2$ is replaced by the whole 2D Euclidian group, and in the denominator $\Bbb Z^2$ is replaced by the whole symmmetry group of the square lattice? What do we get?

I suppose that by the whole 2D Euclidian group you mean the group $G$ of isometries of $\Bbb R^2$. Let $H$ be the group of the elements of $G$ preserving the lattice $\Bbb Z^2$. For our purpose it is convenient to consider elements of $G$ in terms of complex numbers. In the description in terms of $a$ and $\omega$, the elements of $H$ are exactly those with $a\in\Bbb Z^2$ and $\omega\in \{1,-1,i,-i\}$. Since $H$ contains a map $\bar z$, each coset $fH$ of $G/H$ intersects both $G_+$ and $G\setminus G_+$, where $G_+$ consists of maps $z\mapsto a+\omega z$. So we shall study the quotient set $G_+/H_+$, where $H_+=G_+\cap H$.

The group $G_+$ can be identified with the set of pairs $(a,\omega)$, where $a\in\Bbb C$, $\omega\in\Bbb T$, and $\Bbb T=\{z\in\Bbb C:|z|=1\}$. This identification imposes on $G_+$ a topology of a subset of $\Bbb C^2$. Remark that the identification imposes on $\Bbb C\times \Bbb T$ an operation $(a,\omega) (a’,\omega’)=(a’+\omega’ a, \omega\omega’)$ for any $a,a’\in\Bbb C$ and $\omega,\omega’\in\Bbb T$. Taking representatives, we see that $G_+/H_+$ is homeomorphic to a cube $[0,1]^3$ with some identifications of its boundary points. Namely, for each $x,y,z\in [0,1]$, $(0,y,z)\sim (1,y,z)$, $(x,0,z)\sim (x,1, z)$, and $(x,y,0)\sim (y,x,1)$. This is a torus, whose surface we inflated a bit, and then we put it into a high-dimensional space and glue its outer surface with the inner, swapping parallels with meridians.

Answer 2

There's a difference depending on what structure about the lattice you want to consider. As groups, every lattice you mentioned is the same. They're all free Abelian groups generated by two elements, so they're isomorphic to $\mathbb Z^2$. Thus, all the corresponding quotient spaces are the same $\mathbb R^2 /\mathbb Z^2$.

If you are interested in the geometrical structures of the lattices, then you should look at their symmetry groups. In this sense, there are five different kinds of lattices in $\mathbb R^2$:

Their symmetry groups are some of the Wallpaper Groups. These groups have the form $G = \mathbb Z^2 \times D$, where $D$ is a discrete group generated by rotations and reflections.

Then you consider the symmetry group $G$ acting on $\mathbb R^2$. When $D$ is the trivial group, you'll get that $$\mathbb R^2 / G = \mathbb R^2/ \mathbb Z^2 \times D \cong \mathbb R^2/\mathbb Z^2.$$ So you are in the case you mentioned at the very beginning of your question. In general the quotient space $$\mathbb R^2 / G \cong \mathbb T^2/D$$ will be an Orbifold, $i.e.$ a geometric space which is a manifold except for a finite set of points (take a look at the section "orbifold notation" in the previous link). You can perform the intuitive identifications on the fundamental region of your pattern. Moreover, these orbifolds characterize the available symmetries for wallpapers.

All this is very nicely explained in the book "The symmetries of things" by J. Conway, C. Goodman-Strauss and H. Burgiel.