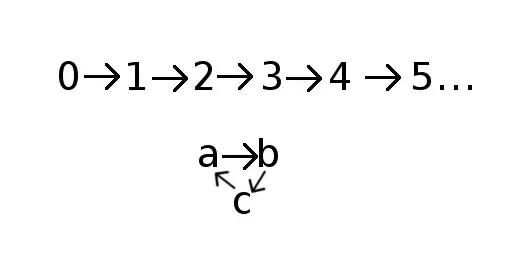Based on the Peano Axioms (wich are a way to correctly absolutely define the set of natural numbers - correct me if i'm wrong) it is possible to construct a set of symbols that doesn't quite look the way i imagine the natural numbers: 
If there is a circle of other symbols next to the infinite row of known natural numbers, doesn't this also fit all the requirements?
So are there multiple unequal sets of natural numbers?
The induction axiom ensures that $\Bbb N$ cannot contain a cycle like your $a,b,c$ cycle. It says that if
then $A=\Bbb N$. Take $A$ to be everything in your diagram except $a,b$, and $c$; this $A$ satisfies both of these requirements, yet it’s not the whole set shown in your diagram. Thus, the set in your diagram doesn’t satisfy the Peano axioms, and indeed they characterize $\Bbb N$.
However, the induction axiom cannot be expressed in first-order logic, and there are structures other than $\Bbb N$ that satisfy the first-order counterpart of the Peano axioms, though they still don’t contain cycles. All of them are linearly ordered and consist of a copy of the standard $\Bbb N$ followed by copies of $\Bbb Z$ (so that everything except $0$ has a unique immediate predecessor). There are restrictions on how these copies of $\Bbb Z$ can be ordered relative to one another. For instance, the only possibility for a countable non-standard model looks like $\Bbb N$ followed by $\Bbb Q\times\Bbb Z$ ordered lexicographically.
If there is a circle of other symbols next to the infinite row of known natural numbers, doesn't this also fit all the requirements?
No. The structure indicated in your diagram violates the axiom of induction:
$$\forall P\subset N:[0\in P \land \forall a\in P: S(a)\in P \implies P=N]$$
This axiom rules out the possibility of set $N$ being comprised of two or more disconnected parts, as in your diagram.
To prove this, we need only the following Peano Axioms:
$0\in N$
$S:N\to N$
Suppose we have $X$, as in your diagram, such that:
$X \subset N\space\space$ (in this case, we have $X=\{a, b,c \}$)
$X\ne \emptyset$
$0\notin X$
$\forall x\in X:\neg \exists y\in N:[y\notin X\land S(y)=x]$
Let $X'=N\setminus X$
It can then be shown that:
$$X'\subset N \land [0\in X' \land \forall x\in X': S(x)\in X'\land \exists x\in N: x\notin X']$$
Generalizing...
$$\exists P\subset N : [0\in P \land \forall x\in P: S(x)\in P\land \exists x\in N: x\notin P]]$$
Or equivalently, we have the negation of the induction principle:
$$\neg\forall P\subset N:[0\in P \land \forall a\in P: S(a)\in P \implies P=N]$$
So are there multiple unequal sets of natural numbers?
If you have two structures $(N,S,0)$ and $(N',S',0')$ that satisfy the 5 Peano Axioms, they can be shown to be essentially identical (order isomorphic). There would exist a bijection $f$ such that:
$f: N\to N'$
$f(0)=0'$
$\forall a \in N: f(S(a))=S'(f(a))$
EDIT:
See my formal proof in DC Proof format (149 lines). There I prove that no non-empty, proper subset $X$ of $N$, like your $\{a,b,c\}$, can be "disconnected" from $N\setminus X$ as you have indicated in your diagram.
The induction axiom is:
If $P(0)$ holds, and if $P(n + 1)$ follows from $P(n)$, then $P$ is true of all values.
If you let $S = \{a, b, c\}$, and $P(n) = n \not \in S$, then the above axiom fails.
$P(0)$ is true, $P(n + 1)$ follows from $P(n)$ (it hold for $n \in S$ due to vacuous implication), but P doesn't hold for all numbers in your structure (it fails for $n \in S$).
So the induction axiom will fail for any structure with non-natural numbers, just let $S$ be the set of numbers not in the natural number chain.
Going by wikipedia. https://en.wikipedia.org/wiki/Peano_axioms
The first 8 axioms (particularly 8): For every natural number n, S(n) = 0 is false. That is, there is no natural number whose successor is 0.) seem to assure that the is the "number line" 0->1->2->3.... and that it is infinite and not circular. But they don't say any thing about there not being any a->b->c->d.... or oom<->pah. which are completely distinct and separate from this set of number lines.
They do state that they must be distinct though. If S(S(S(....(a)))) = a then a $\ne $ S(S(.....(0))))). Or if b $\not \in$ 0->1->2->3.... then no predecessor or successor of b is either.
But 9) the induction axiom does imply there are not distinct threads.
If K is a set such that:
0 is in K, and
for every natural number n, n being in K implies that S(n) is in K,
then K contains every natural number.
As K = 0->1->2->3 ... is such a set we have $\mathbb N \subset K \subset \mathbb N$ and 0->1->2->3.... are precisely the natural numbers and nothing else are.
This is not just theoretical. 1/2 ->1 1/2 -> 2 1/2 -> 3 1/2 $\not \subset \mathbb N$ is just such a separate string that does exist but are not the natural numbers.
I like to think (and I'm probably abusing some theory and I could be wrong) that 1-8 define the smallest thing the natural numbers can be. And the induction axiom restricts it to the smallest it can be. I may be naively abusing math though.
