0

I want to know if the usual Peano axioms can really deal with "problems" like the following loop:

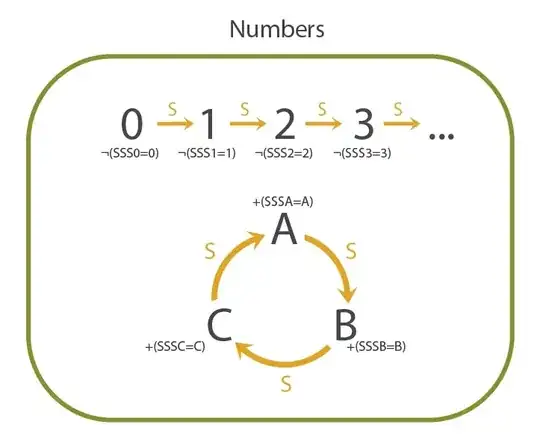
enter image description here

I honestly don't see the axioms avoid the last diagram. Thanks in advice.

Parcly Taxel
  • 103,344
Samuel Díaz
  • 71

3 Answers3

5

Consider the set of numbers $a$ with $SSSa\ne a$. That contains $0$ and is closed under the successor operator. So it is all of $\Bbb N$.

Angina Seng
  • 158,341
  • +1. A quick comment for the OP: to see how you can come up with this, notice that the set of numbers "outside" the loop is an inductive set (= contains $0$ and is closed under successor) which is strictly smaller than the whole structure. Now what the induction scheme in PA does essentially is say that there are no definable inductive proper subsets of the universe, so what we want to do is cook up a definition of this proper inductive set. Thinking along these lines, we come up with the answer above. – Noah Schweber Feb 08 '18 at 14:00
2

What about ordering ?

In $\mathsf {PA}$ we can define:

$m < n \leftrightarrow \exists z \ (n=m+Sz)$.

Then, we can prove: $Sn=Sn+0=S(n+0)=n+S0$, and thus: $\exists z \ (Sn=n+Sz)$, i.e. $Sn>n$.

So, $SSSA > SSA > SA > A$, contradicting the fact that: $SSSA=A$.

Mauro ALLEGRANZA
  • 94,169
  • I believe the question intends the whole diagram to be a putative picture of the natural numbers (or a subset thereof), rather than just the loop in the picture. –  Feb 08 '18 at 07:40
  • Sure, but "m<n↔∃z (n=m+Sz)" is not included in the axioms. Is that some kind of order axiom? – Samuel Díaz Feb 16 '18 at 06:15
0

I understand your point of view Samuel Diaz (the author of the question) because I had the same question: The problem come from the anbigous way to define the 9th axiom of Peano (as you can see it from wikipedia for instance). It must be understood as :

Only N set which satisfy the next truth are really N set: for all set φ (or a unary predicate ie a set) such that: (φ(0) is true, and for every natural number n (belonging to set N), φ(n) being true implies that φ(S(n)) is true) then φ(n) is true for every natural number n.

in other words: N must be a set for which all other sets φ for which (φ(0) and for all n belonging to N: φ(n)=> φ(s(n)) => φ are equal to N.

Indeed in N sets where loop exist, all φ sets which is true for (φ(0) and for all n belonging to N: φ(n)=> φ(s(n) ) (for instance a φ set have all true N numbers and no loops) are not true for ( φ = N) (in this case φ contain only the true n number, and N contains also loops!)

Nicolas Bourdon
  • 1