1

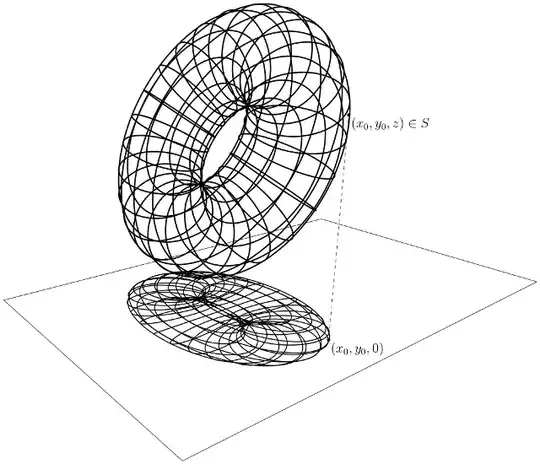
$\newcommand{\Reals}{\mathbf{R}}$I am struggling with the concept of a shadow in $\Reals^3$. My professor provided the class with the following definition:

Given $S \subset \Reals^3$, the Shadow of $S$ in the $XY$ plane is equal to $$\{(x,y,0) | \text{$Z$ ray determined by $(x,y,0)$ hits the solid.}\}$$

This was what was written on the blackboard in my Calculus class. What exactly does this mean, and is there a better way to define a shadow? How does this translate to deriving the shadow for any shape in $\Reals^3$? Does deriving a shadow work differently when considering a cylindrical or spherical coordinate system, and if so, how?

Andrew D. Hwang
  • 78,195
Derek Ehle
  • 196

1 Answers1

1

$\newcommand{\Reals}{\mathbf{R}}$Imagine a light "at infinity" on the $z$-axis: Its rays travel along lines parallel to the $z$-axis. If $S \subset \Reals^{3}$, and if $(x_0, y_0)$ is a point of $\Reals^{2}$, then the ray of light $\{(x_0, y_0, t): t > 0\}$ touches $S$ if and only if there exists a $z > 0$ such that $(x_0, y_0, z) \in S$, if and only if $(x_0, y_0, 0)$ lies in the shadow of $S$.

An object and its shadow

Andrew D. Hwang
  • 78,195
  • 1
    Thanks for the informative answer! That helps me to gain some real insight. If I were to try and paraphrase this into lay mans terms, would it be accurate to say that the shadow of a shape is essentially what would happen if you took the shape and "flattened" it onto the XY plane? – Derek Ehle Oct 20 '16 at 02:20
  • Yes, that's accurate, as long as it's clear that "flatten" is meant in the geometric sense of taking all points $(x, y, 0)$ "beneath" some point of $S$, and not in the physical sense of "crushing" $S$ onto a plane, which typically deforms an object. (E.g., when you step on an aluminum can, the profile is no longer circular.) – Andrew D. Hwang Oct 20 '16 at 03:03