What are the projection maps?

Question

I've read that projection maps are an important type of maps whose domain is a product of n possibly different sets. My question is that why do they name them "projection" maps? What are we projecting exactly? Yes we are mapping or relating the product of the sets to an output (thats what a mapping already is ) but what are we projecting?

Answer 1

Here's an application of projections, called a stereographic projection, that should seem a bit more "concrete" in a way.

This below is the called the inverse stereographic projection, mapping a lower dimension to a higher dimension.

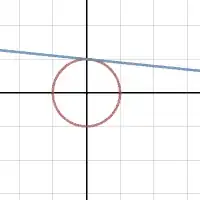
Let's begin like this, I want you to look at the image below first. All it contains is a circle of radius $1$ and a line is in the form $y=mx+1$ with $m$ ranging from $-10$ to $10$.

1. Consider the very top point of the circle, the point $(0,1)$, as undefined.

2. Note that as the slope changes, where the line intersects the circle and the $x$-axis changes as well. In a single snapshot of the gif, let's call the point it intersects on the $x$-axis as $(x_0, 0)$ or just $x_0$ for short. Call the point it intersects on the circle $(x_c,y_c)$

3. Now try to imagine this: in that random snapshot of the gif (where the line is held still) map ("assign") the point $x_0$ to $(x_c,y_c)$. Now go to the next snapshot and do it again, and again, ...

Now let the slope instead of being anything in the range $[-10, 10]$, be anything in $( - \infty, \infty)$. What follows is every single point on the real number line ($x$-axis) gets assigned to a point on the circle! This is the projection aspect. With room to spare even, that point on the top of the circle never got assigned anywhere after all.

Can we find the function of this projection, you say?

Yes! Let's find the function $f$ that tells us where our point $x_0$ goes on the circle. It'll be a function mapping one number to two, or more explicitly, $f: \mathbb{R} \to \mathbb{S} \backslash \{ (0,1) \}$, where $\mathbb{S} \backslash \{ (0,1) \} = \{  x \in \mathbb{R}^2 | x^2 + y^2 = 1, \ \ (x,y) \neq (0,1) \}$.

To get started we need to know what we have to work with. Without loss of generality let's let the radius be $1$ (that is, you can make the radius whatever you please, I just wanted to make it look pretty in the end). What we have is

$$\begin{cases} x^2+y^2=1 \\ y=mx+1 \text{ where } m = -\frac{1}{x_0} \end{cases} $$

which is actually all we need. Let's leave the $m$ in there for now though to avoid having to deal with messy equations, and just remember that our circle doesn't include the point $(0,1)$.

From here it's a matter of some plug and chug.

$x^2+(mx+1)^2=1$

$x^2+m^2x^2+2mx=0$

$(1+m^2)x^2+2mx=0$

$\displaystyle{ x=\frac{-2m \pm \sqrt{4m^2}}{2(1+m^2)}}$

$\implies x=\displaystyle{\frac{-2m}{1+m^2}}$

Great! Now we complete the same procedure for the other coordinate.

$\displaystyle{\left(\frac{y-1}{m} \right) ^2 + y^2 = 1}$

$y^2-2y+r^2+m^2y^2=m^2$

$(1+m^2)y^2-2y+(1-m^2)=0$

$y=\displaystyle{\frac{2 \pm \sqrt{4-4(1+m^2)(1-m^2)}}{2(1+m^2)}}$

$ y= \displaystyle{\frac{1 \pm m^2}{1+m^2}}$

Here we must choose $1-m^2$ for the numerator because otherwise things would simplify to $y=1$, and remember, (0,1) wasn't defined on our circle.

$\displaystyle{ \implies y=\frac{1-m^2}{1+m^2}}$

All this, in summary, provides the following function: $$f(x_0)=\displaystyle{ \left< \frac{-2m}{1+m^2}, \frac{1-m^2}{1+m^2} \right>}$$ which, after plugging in the fact that $m=-\frac{1}{x_0}$ provides...

$$f(x_0)=\displaystyle{ \left< \frac{2x_0}{{x_0}^2+1}, \frac{{x_0}^2-1}{{x_0}^2+1} \right>}$$

And there we have it, any point $x_0$ on the real number line can be mapped to the point $f(x_0)$ on our circle of radius $1$! :)

Now the inverse of our above function, which goes from $\mathbb{S} \backslash \{ (0,1) \} \to \mathbb{R}$ is the stereographic projection, projecting the circle to the real number line.

Try to find the function, which we'll call $g: \mathbb{S} \backslash \{ (0,1) \} \to \mathbb{R}$ yourself.

I'll put the answer below in a spoiler.

It's found as follows: the slope, since we don't have $x_0$, is now given by $\displaystyle{m=\frac{1-y_c}{-x_c}}$. Solving $y=mx+1$ for $x_0$ is done by substituting $y=0$ then some algebra, giving $\displaystyle{x_0 = f^{-1}(x_0) = g(x_c, y_c) = \frac{x_c}{y_c -1}}$.

Also note, by finding the inverse of our above function you've also shown that a circle of radius $1$ has "as many elements" as the real number line ($\mathbb{S} \backslash \{ (0,1) \} \cong \mathbb{R}$) :)

Answer 2

Generally, a projection map "projects" elements onto a lower dimensional subspace which is a product of some subset of those sets. For example, consider the map $(x,y) \mapsto x$ from $\mathbb{R}\times\mathbb{R} \to \mathbb{R}$, which projects onto the first coordinate. If you were to express this graphically, you would see that you can take any point and project it vertically onto its $x$-coordinate, almost as if it were the "shadow" of the point along this vertoca; line.