Starting with
$$
\mathbf{A}x = b,
$$
where the system matrix of rank $\rho$ has $m$ rows, and $n$ columns:
$$
\mathbf{A} \in \mathbb{C}^{m\times n}_{\rho}, \quad
x \in \mathbb{C}^{n}, \quad
b \in \mathbb{C}^{m}.
$$
The general least squares problem is defined as
$$
x_{LS} = \left\{ x \in \mathbb{C}^{n} \colon \lVert \mathbf{A}x - b\rVert_{2}^{2} \text{ is minimized}\right\}
$$
and the solution is
$$
x_{LS} = \color{blue}{\mathbf{A}^{\dagger} b} + \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger}\mathbf{A} \right)y}, \quad y\in\mathbb{C}^{n}.
$$
Range space components are in blue, nullspace in red.
The set of least squares minimizers is an affine space (dashed red line) passing through the range space of $\mathbf{A}$ at the point $x_{LS} = \mathbf{A}^{\dagger}b,$ as seen in the figure.
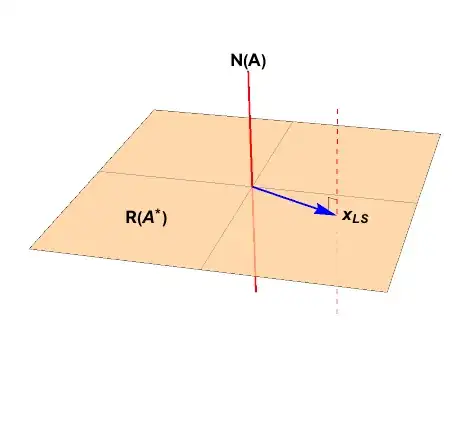
Every point on the dashed line is a least squares minimizer. Which point has minimum length? That is, which point is closest to the origin?
$$
\lVert x_{LS}(y) \rVert_{2}^{2}
= \lVert \color{blue}{\mathbf{A}^{\dagger} b} + \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger}\mathbf{A} \right)y} \rVert_{2}^{2}
= \lVert \color{blue}{\mathbf{A}^{\dagger} b} \rVert_{2}^{2}
+ \lVert \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger}\mathbf{A} \right)y} \rVert_{2}^{2}
$$
We can control the nullspace term in red by selecting the vector $y=0$; this choice is the least squares minimizer of minimum norm, $\color{blue}{\mathbf{A}^{\dagger} b}.$
Notice that the nullspace is trivial $\color{red}{\mathcal{N}\left( \mathbf{A} \right)}=\left\{ \mathbf{0}\right\}$ when $n=\rho$. Therefore, the set of minimizers is a point, and the solution is unique.
