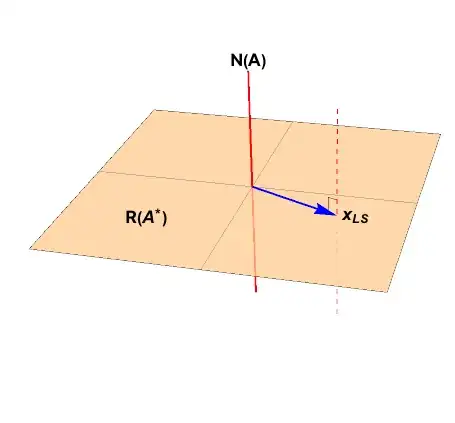
recently I have a linear system $A\mathbf{x}=\mathbf{b}$ to solve. Suppose $A^\dagger$ is the Moore-Penrose inverse of $A$. If $A$ is overdetermined, i.e. more rows than columns, then $\mathbf{x}=A^\dagger\mathbf{b}$ is the unique least squares solution. If $A$ is underdetermined, i.e. more columns than rows, though there are infinitely many solutions, then $\mathbf{x}=A^\dagger\mathbf{b}$ is the unique solution with minimum norm.
Is my understanding right? Thanks for help!