If calculus is just based on minute approximations, can't it be wrong?

Question

Recently I've started my calculus classes and till now what I've seem to understood is that calculus is basically finding solutions by approximations on a microscopic level.

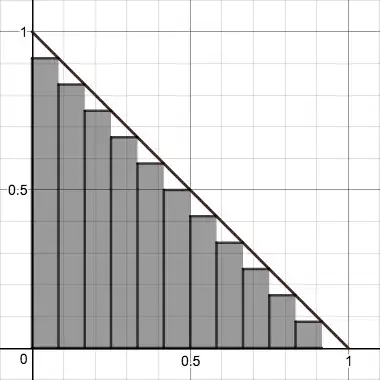
So if I have to find find the area covered by a circle, I would need to fit in many (~infinite) triangles (or rectangle) such that their edges appear to be matching with the circle. And now all I need to do is to sum the area of all these, infinite, triangles since we already know their area.

In the above example, we've just seem to approximated that their edges super impose with the circle's curve. If we still zoom in then most probably we could fit in more such triangles.

And this is where my confusion is, at some point, the answer won't be perfect. It would just be a very very close approximation to the actual area of circle. So, doesn't this mean that calculus is an inefficient way?

And oh btw, the above example is based on https://en.wikipedia.org/wiki/Method_of_exhaustion

Let me give another example. Consider a square of 1 unit. The shortest path to travel from one end to another would cover sqrt(2), using Pythagoras theorem. The longest way would be to go through the sides, which will be 2 units. But if we were to choose any other path except the diagonal and which also doesn't crosses itself neither goes back, then also the distance covered would be 2 units. Yes, any path, inside the square would also cover 2 units. Now, consider that you're going in zig zag manner and also very close to the diagonal. As shown in this picture.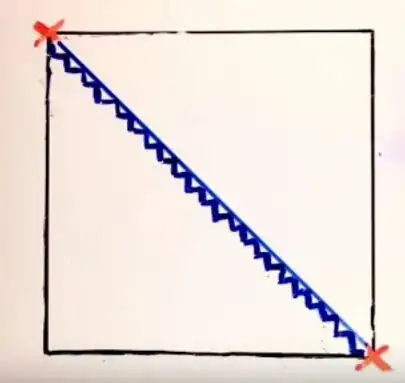

Now, make those zig-zag paths more small. So small that it finally appears to be a straight line, i.e. diagonal. Remember, it is still zig-zag on microscopic level. And over here we meet a paradox. Pythagoras says that its length is sqrt(2) however, choosing any path within square that doesn't crosses and neither goes back should provide the distance as 2 units.

This is something that I'm finding very hard to digest. Does this somewhat hints that calculus isn't the best way out there or maybe, calculus has its own flaw?

Thank you for putting in your efforts to answer this question.

Answer 1

First of all calculus is not based on minute approximations and processes of calculus are exact as $1 + 1 = 2$. On the other hand many of the approximation techniques have their theoretical justification via processes of calculus.

There is also another common fallacy to identify the thing being approximated with one of the approximations to it. Thus the area of a circle is a well defined thing and areas of inscribed polygons are an approximation to the area of circle. In this particular case the the area of the circle is not equal to any of the aproximations obtained via area of inscribed polygons. This does not mean that the area of circle itself is something undetermined.

---

While we are on topic of approximations, it makes sense to simplify the problem considerably. Consider the following hypothetical situation. Suppose you have a cake and you want to divide it into $3$ equal pieces, but suppose the only tool allowed is some machine which can cut any given object into $10$ equal pieces. How do you use the machine to divide the cake into $3$ equal pieces?

On a first glance it appears that it is not possible to do anything about it. But perhaps there is a way out. First divide the cake into $10$ pieces (call these pieces of level $1$) and take $3$ pieces out of it. Then take next piece and divide it further into $10$ pieces (call these pieces of level $2$) and take three pieces of level $2$ and keep it together with the $3$ pieces of level $1$ already taken. Combined these $3$ pieces each of level $1$ and $2$ do not exactly make $1/3$ of the original cake, but if we keep on repeating this process to many levels we are getting to a better and better approximation of $1/3$ of the original cake. Note that in a finite amount of time (finite number of levels) this process will never exactly yield $1/3$ of the original cake, but this does not imply that the idea of $1/3$ of the cake is not perfect/exact.

But the question remains how do we make sense of $1/3$ in terms of a process which can only handle division by $10$? Here is the bold and beautiful idea: $1/3$ is not equal to any of the numbers obtained using division by $10$ in a finite number of steps, but rather it represents the infinite process of dividing by $10$ and taking $3$ out of it for ever.

---

The idea of a real number (which is the basis of calculus) is also in the same spirit. A real number is defined in terms of set of rational numbers each of which is an approximation to the real number being defined. And here a finite set of approximations can't do the job, but rather by definition we always require the set of approximating rationals to be an infinite set.

The theme of last paragraph is a recurring one in whole of calculus and it is embodied in the idea of concept of a limit. The notation $\lim_{x \to a}f(x) = L$ means that values of $f$ is near $L$ when values of $x$ are near $a$, but this is only a crude meaning of the limit concept. The true meaning is that the values of $f$ can be made to lie as near to $L$ as we please for all values of $x$ sufficiently near $a$. Thus a limit notation is again equivalent to an infinite number of statements about values of $f$ near $x = a$.

I think the very nature of dealing with infinity is the main stumbling block in the way of true appreciation of the processes of calculus. The area of a circle is not equal to the area of any one of the specific inscribed polygons, but the area of a circle can be identified with the set of areas of all inscribed polygons.

---

The analysis of length is somewhat different from that of an area and it starts by taking length of a line segment as granted and hence there is no point in trying to approximate the length of a line segment using a zig-zag path. Once the length of a line segment is available the length of a curve is defined by means of the length of all possible polygonal arcs obtained by joining a finite number of points on the curve.

Notice that even in case of a curve the zig-zag path is not used to define the length. We use polygonal paths only and the vertices of the polygon must lie on the curve whose length is being defined. The problem with zig-zag paths is that no matter how small the step size, length of the zig-zag path exceeds the length of curve by a wide margin (this is easily seen in your example if you focus closely on one step: if $ABC$ is a right triangle with right angle at $B$ then sum of $AB$ and $BC$ is a much worse approximation to the length of hypotenuse $AC$).

Answer 2

In J.G.’s comment to your question, he highlights a crucial concept that you’re missing which is worth elaborating. The successive approximations to a value have to be “good” in a specific sense. Namely, the error in the approximation—the difference between it and the true value—has to eventually start getting smaller as you refine the approximation. Not only does it have to get smaller, but it has to get smaller “fast enough.” This is a stronger requirement than the series of approximations just having a limit.

In the case of the stairstep approximation to the length of a square’s diagonal, observe that, since the length of every stairstep path is 2 units, any sequence of finer and finer approximations trivially has a limit: 2. However, not only does the error in the approximation not get smaller fast enough, it doesn’t get smaller at all! These approximations aren’t “good,” so they’re inappropriate from the point of view of calculus (and there’s no paradox).

Answer 3

I believe that the true power of calculus comes from limits. You're right that all of these methods in calculus are based on increasingly accurate approximations. However, what makes them correct is the fact that we can use limits to determine the exact value that a sequence of approximations is approaching. Limits are well-defined, precise, and correct through epsilon-delta proofs.

In reference to your second question, I think this link should help. I especially like the second explanation. The reason this method does not work has to do with the way we determine the length of a curve. Arc-length is defined in terms of derivatives, so two curves which approach each other (but have different derivatives) may have different lengths.

Answer 4

I think you may be looking at your zig-zag example the wrong way. Instead of looking at the length of the zig-zag, let's look at the area under it:

Say the zig-zag is made up of $n$ rectangles, like in the picture above. The area of the $k$th box from the right would be the following: $$\frac{k-1}{n}\cdot\frac{1}{n}=\frac{k-1}{n^2}$$

So, the area of under the zig-zag can be written as so: $$\sum_{k=1}^{n}\frac{k-1}{n^2}=\frac{n(n-1)}{2n^2}$$

Notice what happens when $n$ gets really really big? The $-1$ becomes negligible, so the area becomes the following: $$\frac{n^2}{2n^2}=\frac{1}{2}$$

This is the area of the triangle. Now, I bet you think that this stupid because "you can't just ignore the $-1$."

This is where the concept of limits comes in. What we want to do is compute the following: $$\lim_{n \to \infty} \frac{n(n-1)}{2n^2}$$

Let's call this value $M$. We define $M$ to be the value for which the following is true:

For any $\epsilon$, there exists an $N$ such that $n>N$ implies $\displaystyle \left|\frac{n(n-1)}{2n^2}-M\right|<\epsilon$.

Pause and ponder why we define this limit in such a manner.

We want to show that $\displaystyle M=\frac{1}{2}$. We can do this by setting $N$ to be equal to $\displaystyle \frac{1}{2 \epsilon}$: $$\left|\frac{n(n-1)}{2n^2}-\frac{1}{2}\right|=\frac{1}{2n}<\frac{1}{2\cdot\frac{1}{2\epsilon}}=\epsilon$$

So, we say that a $n$ approaches infinity, the area of under the zig-zag approaches the area of the triangle.

If the length of the zig-zag thing is bothering you, let me try to explain: Nobody would approximate the length of the diagonal like that. In calculus, we use something else: $$\int_a^b \sqrt{1+\left[f'(x)\right]^2}dx$$

In this case, $a=0$, $b=1$, and $f(x)=-x+1$. If you compute this, you get $\sqrt{2}$.

Answer 5

The problem is that you are focused on the individual approximations. The big important idea you're missing is that by looking at all of the approximations, you can exactly determine what they are approximating.

For example, the very simplest form of the idea underpinning the method of exhaustion is the following problem:

Suppose that $x$ is a number with the properties that:

• $x$ is bigger than every negative number
• $x$ is smaller than every positive number

Find $x$.

The answer, of course, is that $x=0$.

---

In the second example, the "paradox" is really just a proof that you can't good approximations this way. More precisely, it proves that no matter how you set up the analysis, at least one of the following statements will be false:

• The sequence of zig-zags converges to the diagonal
• Length is a continuous function

Answer 6

The original poster says: "Yes, any path, inside the square would also cover 2 units." How do they justify this claim?

Edit: Here's one possible answer to the original poster's problem.

Oh, I see! I believe the problem you're pointing at is as follows. Assume: we live on a discrete finite lattice with a minimal element of length 1. Then, there will be no square root of 2, i.e. there would be no diagonal of an elementary square. Consequently, your conclusion would follow. However, if you admit the existence of the diagonal, therefore admitting the existence of the square root of 2, the problem disappears.

Let's construct such set of real numbers.

Consider a unit interval $\left[0,1\right]$ on a real number line. Let there be $c$ elements of $R$ on $\left[0,1\right]$. Number $c$ is infinitely large, of course. We just assume that one is allowed to do arithmetics with it. One such $c$ would be, say, Cantor's continuity $c$, the cardinal number of $R$. So, we conclude here that the idea of the existence of $c$ is fairly familiar and plausible.

Let us ask the following question now: "What is the smallest distance between two elements of $R$?" This question may seem strange at first, but the answer is rather straight-forward. Namely, one simply divides the length of the unit interval, $1$, by the number of elements $c$, obviously, to calculate the smallest distance $d$. The result is $d=1/c=0$. The distance is $0$ because $c$ is infinitely large. In other words, set $R$ is dense. There is no smallest distance.

Now stretch the unit interval by factor $c$! The unit interval is of length $c$ now. If one assumes that the number of elements hasn't changed, then the number of elements on the unit interval is still $c$. Hence, the smallest distance is now $d=c/c=1$. There is the smallest distance now. Notice that the unit interval is just stretched by factor $c$, assuming the number of elements remained intact during stretching. It's the same unit interval from $R$ we are used to, but magnified, as if seen under the looking glass of magnification $c$.

If done like this, then the new set we created by stretching $R$ is no longer dense. One way to look at this phenomenon is to conclude that $R$ is dense relative to one measure, but not relative to another measure.

Let's denote the stretched set by $R_l$, with $l$ standing for "larger". Some rather interesting properties are exhibited by $R_l$. For instance, lengths of curves in $R_l^2$ depend on orientation. This is simply due to the fact that $R_l$ is discrete. Another interesting property is that $R_l$ is well ordered now. Yet another interesting property is that $R_l$ has the smallest element, and this smallest element can be interpreted as an infinitesimal in $R$. Yet another interesting property is that one my accommodate another unit interval from $R$ with $c$ elements, onto the unit interval on $R_l$, having only two elements, $0$ and $1$, in $R_l$, thus creating a dense set once again. Let's call this new dense set $R_{lD}$, with $D$ standing for "dense". Any function defined on $R$ is not defined at all points of $R_{lD}$. In other words, functions continuous on $R$ are not necessarily continuous on $R_{lD}$. The converse statement is also true: functions discontinuous on $R$ may be continuous on $R_{lD}$, depending on how one extends them from $R$ onto $R_{lD}$.

So, you see, the original poster's question may hide some interesting hidden assumptions with some interesting properties. I hope this clarifies my point of view a bit.

Answer 7

You are right, but note that in calculus we don't use just minor approximations, we use a very powerful tool called a limit. Suppose you want to calculate the area of a circle through the method of exhaustion by using the polygon technique, in which we keep on increasing the number of sides of the polygon, so that it becomes closer and closer to the perimeter of the circle. If you stop at a point, then yes, microscopically, it will still be a polygon, but what we usually say is that $$\lim_{n\to\infty}Area(n)=Area(circle)$$, where $n$ is the number of sides of the polygon, and $Area(n)$ denotes the area of that $n$-sided polygon. What you are doing, is stopping in between, which is not a limit. Keep on continuing indefinitely, and then you will indeed get the "exact" area, but keep on continuing, on and on and on(which is a very stupid process). The beauty of calculus is the notion of a limit, which makes it accurate, exact and easier to perform.

Answer 8

Let me ask you a question, the true value of anything, can you not approximate it to any desired degree? If it's incorrect our attempts to approximate the real value would at somepoint have a lower bound on the error, as our approximation tends toward one value the incorrect one is distinctly different.

That is what calculus does, by using a method of approximation it finds the true value by finding the one exact value we can approximate to any desired degree. That is in a simple way the whole idea behind the concept of calculus.

Your example however does not even remotely approximate a straight line side. Just because we might "see" it as being a straight line between the points doesn't make it so mathematically. What you got infact is what some call an infinigon or a fractal which is a completely different beast. To be properly used it must MATHEMATICALLY approximate it to any degree, not just human eyes and your method never does that which is why it gives such bad results.

Answer 9

Is probably worth noting ALL calculations with irrational numbers are effectively approximations with arbitrary precision.

Suppose $A=\{ x \in \mathbb Q, x^2<2\}$

It can be shown $1 \in A, x\in A \implies \frac{x+2/x}{2}\in A$ and $1<x^2<(\frac{x+2/x}{2})^2<2$. It follows that for any element in $A$, there's a greater element which nonetheless has a square less than $2$.

Suppose $\epsilon_1>0 , x \in A , \sqrt{2}-\epsilon_1<x<\sqrt{2}$. Then $\exists \epsilon_2>0, \sqrt{2}-\epsilon_2<\frac{x+2/x}{2}< \sqrt{2}, \epsilon_2<\epsilon_1$.

By induction is follows $\forall \epsilon>0, \exists x\in A, \sqrt{2}-\epsilon<x< \sqrt{2}$. In other words, $\sqrt{2}$ can be approximated with a rational number with arbitrary accuracy. From here we assert the existence of the real number itself.

---

Suppose we have prime numbers $p$ and $q$.

By the above we can have quantities $\epsilon_1, \epsilon_2>0$

$\sqrt{p}-\epsilon_1<x<\sqrt{p}$

$\sqrt{q}-\epsilon_2 < y < \sqrt{q}$

$\sqrt{p}+\sqrt{q}-\epsilon_1-\epsilon_2<x+y<\sqrt{p}+\sqrt{q}$

If two irrational numbers can be approximated arbitrarily closely, then so can their sum. This leads to a way of defining arithmetic with irrational numbers using approximations of rational numbers.

However, the approximation has an error term that can be made arbitrarily small. We conclude two quantities are equal if the absolute value of their difference is smaller than any positive number you can offer.

From this definition of the reals we can generate a similar concept for curves in $\mathbb R \times \mathbb R$, i.e. functions.

Approximations are used to prove equality. In practice though, you can only ever approximate real numbers, and so calculations themselves lead to approximations. Principle here established in real analysis can help you bound error terms in those approximations. Taking those into account you can it your tolerances even if you use only approximations.

Taking all that into account, you get a general, rigorous theory of limits, and from there justify what we do in calculus.