From the easy identity $(n+1)^2-(n-1)^2=4n$, we deduce
$$n^3=\frac{n^2(n+1)^2-n^2(n-1)^2}4=S_n-S_{n-1}.$$
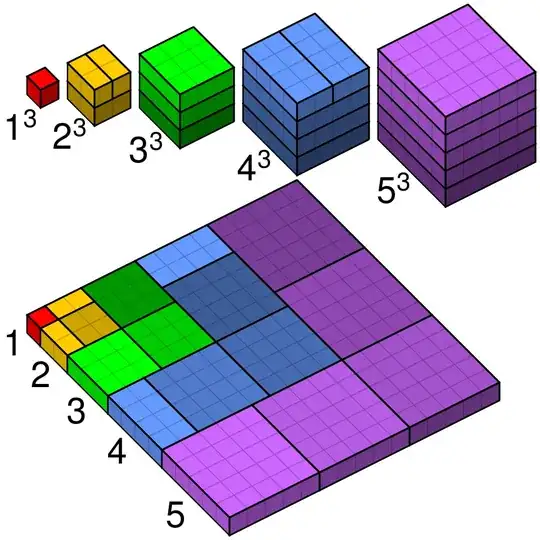
By telescoping, the sum of consecutive cubes is always a difference of squares.
In particular, the sum of the first cubes is always a perfect square.
Then, it should be intuitive that the sum of the $p^{th}$ powers of the integers are polynomials of degree $p+1$, and comparing to integrals, the leading term must be
$$\sum_{i=1}^n i^p\sim\frac{n^{p+1}}{p+1}.$$
So, looking for a case such that $$\left(\frac{n^{p+1}}{p+1}\right)^2=\frac{n^{q+1}}{q+1}$$
we find the only solution
$$\left(\frac{n^2}2\right)^2=\frac{n^4}4$$ giving identical asymptotic behaviours.
Combining the previous two properties, the two sequences must coincide exactly.