For which $n \in \mathbb{N}$ do we have $\sum\limits^n_{k=0} k^3 = (\sum\limits^n_{k=0} k)^2$?

Question

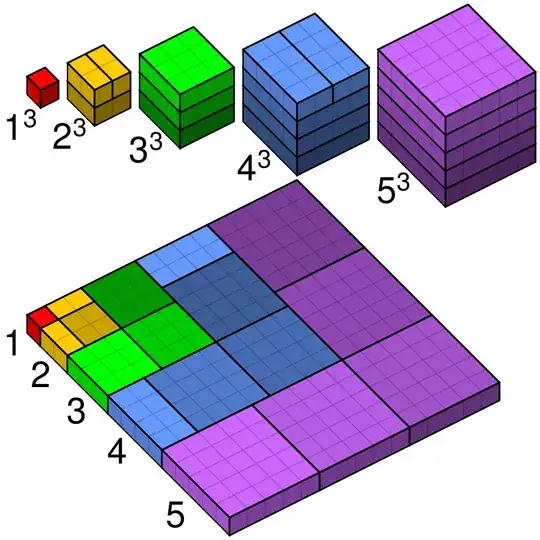
I have a question that I don't know how to solve.

For which $n \in \mathbb{N}$ do we have $$\sum\limits^n_{k=0} k^3 = (\sum\limits^n_{k=0} k)^2\quad ?$$.

Here's what I've tried:

\begin{align*}\sum\limits^n_{k=0} k^3 = (\sum\limits^n_{k=0} k)^2 & \Leftrightarrow 1+8+27+\cdots+n^3 = (1+2+3+\cdots+n)^2\\ & \Leftrightarrow \sqrt{1+8+27+\cdots+n^3} = 1+2+3+\cdots+n \end{align*}

You can use induction and $\sum_{i=1}^n i = \frac{1}{2}n(n+1)$ for $n\in \mathbf N$. — , Aug 15 '16 at 08:15
Have a look here: http://math.stackexchange.com/questions/1882161/intuitive-reason-for-why-left-displaystyle-sum-i-0n-i-right2-displays/ — Robert Z, Aug 15 '16 at 08:18
Have a look at Bernoulli's three theorems for expansion of sums, if you are interested. — Akshar Gandhi, Aug 15 '16 at 08:40

Yiorgos S. Smyrlis · Accepted Answer · 2016-08-15T08:30:21.850

5

It holds for all $n\in\mathbb N$. Is this sufficiently convincing:

Note. This formula has been known for 2000 years. It is due to Nicomachus of Gerasa.

edited Aug 15 '16 at 08:30

answered Aug 15 '16 at 08:22

Yiorgos S. Smyrlis

83,933

score 0 · Answer 2 · edited Apr 13 '17 at 12:21

0

There is a formula for the LHS (sum of consecutive cubes -- proof here) that says it's equal to $\left(\frac{n(n+1)}{2}\right)^2$, which is therefore equal to the RHS for all $n \in \mathbb{N}$

edited Apr 13 '17 at 12:21

Community

1

answered Aug 15 '16 at 08:20

Ken Wei

1,759

For which $n \in \mathbb{N}$ do we have $\sum\limits^n_{k=0} k^3 = (\sum\limits^n_{k=0} k)^2$?

2 Answers2