Is there a known geometric proof for this famous problem? $$\zeta(2)=\sum_{n=1}^\infty n^{-2}=\frac16\pi^2$$
Moreover we can consider possibilities of geometric proofs of the following identity for positive even inputs of the Zeta function: $$ \zeta(2n)=(-1)^{n+1} \frac{B_{2n}(2\pi)^{2n}}{2(2n)!}$$ and negative inputs: $$ \zeta(-n)=-\frac{B_{n+1}}{n+1}$$
Yes, there is a geometric proof for $\zeta(2)=\sum_{n=1}^\infty n^{-2}=\frac16\pi^2$, and, on top of that, it is a very unusual and, in my opinion, beautiful one.
In his gorgeous paper "How to compute $\sum \frac{1}{n^2}$ by solving triangles", Mikael Passare offers this idea for proving $\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}$:
Proof of equality of square and curved areas is based on another picture:
Recapitulation of Passare's proof using formulas is as follows: (for each step there is a geometric justification)
$$\sum_{n=1}^\infty \frac{1}{n^2} = \sum_{n=1}^\infty \int_0^\infty \frac{e^{-nx}}{n}\; dx\; = -\int_0^\infty log(1-e^{-x})\; dx\; = \frac{\pi^2}{6}$$
I'm not sure what you mean by a geometric proof, but the following should fit the bill, as here the identity is deduced from a comparison of two areas: the first area is
$\displaystyle\int_{[0,1]^2} \frac{1}{1 - xy} \frac{dx dy}{\sqrt{xy}}$
and the second is
$4 \displaystyle \int_{\substack{\xi, \eta>0 \\ \xi \eta \leq 1}} \frac{ d \xi \, d \eta}{(1+\xi^2)(1+\eta^2)}$;
They are equal by a change of variables. For the first quantity, expand $(1-xy)^{-1}$ as a geometric series and integrate term-wise to get $3 \cdot \zeta(2)$. The second can be computed to $\pi^2/2$. This can be found in detail in Kontsevich and Zagier's Periods (bottom of page 8), where they attribute the idea to Calabi. (You should easily be able to hunt down an identity of $\zeta (n)$ being equal to an integral over the unit square in $\mathbb{R}^n$, like the first above. It might be a fun exercise to see if this idea is can be adapted for even $n$.)
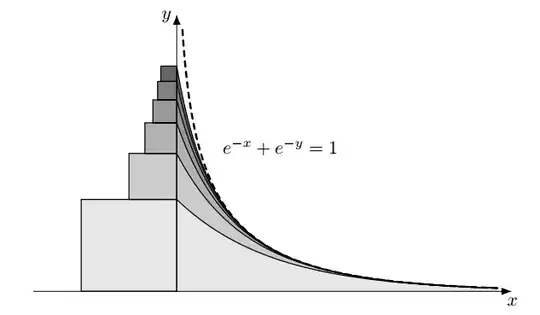
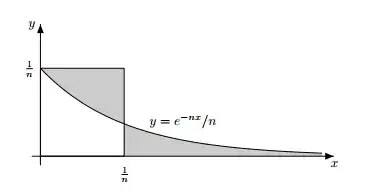
One geometric/probabilistic proof is by Eugenio Calabi.
Consider the double integral $$I=\int_{0}^{1}\int_{0}^{1} \frac{1}{1-x^2y^2} \ dy \ dx.$$ Expand the integrand into a geometric series as such $$ \frac{1}{1-x^2y^2} =\sum_{n=0}^{\infty} (xy)^{2n},$$ which is justified by the region of integration, that is $0<x,y<1.$ Exchange summation and integration (application of Tonelli's theorem), and integrate term by term to get $$I=\sum_{n=0}^{\infty} \frac{1}{(2n+1)^2}.$$ Now, we evaluate $I$ directly. Make the change of variables $$x=\frac{\sin(u)}{\cos(v)}, y=\frac{\sin(v)}{\cos(u)}.$$ This transformation has Jacobian Determinant $$\frac{\partial (x,y) }{\partial(u,v)}=1-x^2y^2,$$ which cancels with the integrand, and the region becomes the open triangle defined by the inequalities $$u+v<\frac{\pi}{2}, u, v>0$$ We know from geometry that this triangle has base $\frac{\pi}{2}$ and height $\frac{\pi}{2},$ hence the area is $\frac{\pi^2}{8}.$ Hence $I=\frac{\pi^2}{8}.$ Now to obtain $\zeta(2),$ we use the fact that $$\zeta(2)=\sum_{n=1}^{\infty} \frac{1}{n^2} = \sum_{n=1}^{\infty} \frac{1}{(2n)^2}+\sum_{n=0}^{\infty} \frac{1}{(2n+1)^2},$$ which implies by some algebraic manipulation that
$$\zeta(2)=\frac{4}{3}I=\frac{\pi^2}{6}.$$
We can extend this proof to the $\zeta(2k).$ Let
$$I_{2k}= \int_{0}^{1}... \int_{0}^{1} \frac{1}{1-x_1^2 \dots x_{2k}^2} \ dx_{2k} \ ... \ dx_1.$$
Converting this integrand into a geometric series and exchanging summation and integration gives the sum: $$I_{2k}=\sum_{n=0}^{\infty} \frac{1}{(2n+1)^{2k}}.$$ We can then recover $$\zeta(2k)=\frac{2^{2k}}{2^{2k}-1} I_{2k},$$ by observing $$\zeta(2k)= \sum_{n=1}^{\infty} \frac{1}{(2n)^{2k}} + I_{2k},$$ and using some algebraic manipulation.
On the other hand, we make the change of variables $$x_i=\frac{\sin(u_i)}{\cos(u_{i+1})}, 1 \leq i \leq 2k,$$ and $u_{2k+1}:=u_{1}$ here. This transformation turns out to have a Jacobian Determinant which cancels with the denominator of the integrand in $I_{2k}.$ The region of integration becomes the open polytope: $$\Delta^{2k}= \left \lbrace (u_1, \dots, u_{2k}): u_{i}+u_{i+1} < \frac{\pi}{2}, u_i>0, 1 \leq i \leq 2k \right \rbrace$$ in which $u_{2k+1}:=u_1.$ Computing the volume of this polytope is much more difficult. Rescaling with the change of variables $u_i=\frac{\pi}{2} v_i,$ and letting $V_1, \dots, V_{2k}$ being $2k$ independent, uniformly distributed random variables on $(0,1),$ we get
$$I_{2k}=\text{Vol}(\Delta^{2k})=\left(\frac{\pi}{2}\right)^{2k} \text{Pr} \left( V_1+V_2<1, \dots, V_{2k-1}+V_{2k}<1, V_{2k}+V_{1}<1 \right),$$ the probability that $V_1, \dots, V_{2k}$ have cyclically pairwise consecutive sums less than $1.$
In the literature, the aforementioned probability has been computed in several ways (see: https://www.maa.org/sites/default/files/pdf/news/Elkies.pdf https://arxiv.org/pdf/1003.3602.pdf https://pdfs.semanticscholar.org/35be/01e63c0bfd32b82c97d58ccc9c35471c3617.pdf)
Joshua Seaton also mentioned Zagier's and Kontsevich's reproduced Calabi proof. The general version of this is to evaluate
$$J_{2k}= \int_{0}^{1}... \int_{0}^{1} \frac{1}{\sqrt{x_1 \dots x_{2k}}(1-x_1 \dots x_{2k})}\ dx_{2k} \ ... \ dx_1.$$
A quick substitution shows $J_{2k}=2^{2k}I_{2k}.$ The generalized version of the change of variables is
$$x_i=\frac{\xi_i^2(1+\xi_{i+1}^2)}{1+\xi_i^2}, \dots, x_{2k}=\frac{\xi_{2k}^2(1+\xi_{1}^2)}{1+\xi_{2k}^2},$$ and upon computing its Jacobian Determinant, we get that
$$J_{2k}=\int_{\mathbb{H}^{2k}} \frac{1}{\xi_1^2+1} \dots \frac{1}{\xi_{2k}^2+1} \ d \xi_{1} \dots d \xi_{2k},$$ where $\mathbb{H}^{2k}$ is the hyperbolic defined by the inequalities: $$\xi_{i}\xi_{i+1} <1, \xi_i>0,$$ where $1 \leq i \leq 2k$ and $\xi_{2k+1}:=\xi_1.$ Letting $\Xi_1, \dots \Xi_{2k}$ be $2k$ independent, nonnegative Cauchy random variables, we get
$$I_{2k}=\left(\frac{\pi}{2}\right)^{2k} \text{Pr} \left( \Xi_1\Xi_2<1, \dots, \Xi_{2k-1}\Xi_{2k}<1, \Xi_{2k}\Xi_{1}<1 \right),$$ the probability that $\Xi_1, \dots, \Xi_{2k}$ have cyclically pairwise consecutive products less than $1.$
In my paper, I show that the probabilities lead to a very gargantuan formula:
$$I_{2k}=\sum_{n=0}^{\infty} \frac{1}{(2n+1)^{2k}}= \left(\frac{\pi}{4} \right)^{2k} +\left(\frac{\pi}{4} \right)^{2k} \sum_{n=1}^{k} \sum_{\substack{(r_1, \dots, r_n) \in [2k]^n: \\ |r_p-r_q| \notin \lbrace 0,1,2k-1 \rbrace, \\ p,q \in [n]} } \prod_{i=1}^{n} \frac{1}{i+\sum_{j=1}^{i} \alpha_j},$$ where $[m]:= \lbrace 1, \dots, m \rbrace$ and $$\alpha_j=2- \delta(2k,2) - \sum_{m=1}^{j-1} \delta(|r_m-r_j|,2)+\delta(|r_m-r_j|,2k-2)$$ and $\delta(a,b)$ is the Kronecker Delta Function. In particular, the inner sum is taken over all tuples $(r_1, \dots, r_n) \in [k]^ n$ having cyclically pairwise nonconsecutive entries.
