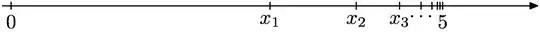Recursive Sequence $a_n = \frac{1}{2} (a_{n-1} + 5) $

Question

I got this question in which they ask me to explain why it is convergent and evaluate its limit.

$$a_1=3\;and\;a_n = \frac{1}{2} (a_{n-1} + 5) \\ n=2,3,4,... $$

To prove it's convergent, I show that it is increasing and bounded above by 5. Also, I find its limit by showing that

Let $L=\lim_{n\to\infty} a_n$

Notice that $a_n = \frac{1}{2} (a_{n-1} + 5)$

Hence $\lim_{n\to\infty} a_n = \lim_{n\to\infty} \frac{1}{2} (a_{n-1} + 5)$

$\Rightarrow L = \frac{1}{2}(L+5)$

$\Rightarrow 2L = L+5$

$\Rightarrow L = 5$

As the sequence is non-decreasing, $$L =\lim_{n\to\infty} a_n=5 $$

That's what I got. However, the book's answer for this question's limit is $\frac{5}{2}$

Is there anything wrong with my proof?

Thanks in advance.

Nothing wrong with the outline, and the limit is indeed $5$, — André Nicolas, Jun 04 '16 at 04:53
I don't see any mistake...just don't forget to prove that it is increasing(it might be a printing mistake in the book). — Coherent Sheaf, Jun 04 '16 at 04:54
To see why this is true, you might wanna read Bartle and Sherbert — Bijesh K.S, Jun 04 '16 at 06:17

WW1 · Answer 1 · 2016-06-04T06:12:31.973

2

It might help to solve the recurrence relation

Define $b_n\equiv a_n+c$ and find the value of $c$ that makes $b_n$ a geometric sequence

$$a_n = \frac{1}{2} (a_{n-1} + 5)\implies b_n-c = \frac{1}{2} (b_{n-1}-c + 5)$$

$$\implies b_n = \frac{1}{2} b_{n-1}-\frac c2 + \frac 52 +c$$ $$\implies b_n = \frac{1}{2} b_{n-1} + \frac {c+5}2$$

SO if $c=-5$ we have $ b_n = \frac{1}{2} b_{n-1} $ which is a geometric sequence having solution

$$ b_n = b_1 \left( \frac 12\right) ^{n-1}$$

Where $b_1=a_1-5 = 3-5 = -2$

So $$ a_n = b_n + 5 = 5 -2 \left( \frac 12\right) ^{n-1}=5 - \left( \frac 12\right) ^{n-2} $$

edited Jun 04 '16 at 06:12

answered Jun 04 '16 at 06:01

WW1

10,497

1

How come that formula doesn't produce $a_1=3$? – user5713492 Jun 04 '16 at 06:07
1

I wrote $(\frac 12)^n $ instead of $(\frac 12)^{n-2}$ in my last line, I have now corrected this. – WW1 Jun 04 '16 at 06:14

score 2 · Accepted Answer · edited Apr 13 '17 at 12:21

You can view the given recurrent sequence in this way: The $(n+1)$-th term is the average of $n$-th term and $5$. From this it is relatively easy to see that the distance from $5$ will be halved in each step. And this can be verified by a direct computation: $$5-a_{n+1} = 5- \frac{a_n+5}2 = \frac{5-a_n}2.$$

As already explained in another answer, you get from this that $(5-a_n)$ is a geometric sequence which tends to zero for $n\to\infty$.

Another way to visualize this is notice that you have $a_{n+1}=f(a_n)$ for $$f(x)=\frac{5+x}2.$$ This gives the following picture

In this case, the function is very simple, so maybe this is more complicated than other solution. But it is perhaps useful to know that if the function $f(x)$ fulfills some conditions, then the sequence determined by $a_{n+1}=f(a_n)$ will always converge to the solution of $f(x)=x$. Look up Banach fixed-point theorem for more information.

But even without relying on some theorem, if the function is simple enough and you can plot it, you can see from the graph whether these iterations converge to $f(x)=x$. You can find picture illustrating this for various functions here. Some of them are taken from related posts:

And I will also add that such diagrams are called cobweb plots.

Very good answer +1 for the graph. "maybe this is more complicated" but it gives more insight to why such sequences will converge. — Paramanand Singh, Jun 05 '16 at 03:33

score 1 · Answer 3 · answered Jun 04 '16 at 05:05

Your work is correct (though of course to have a complete proof you need to include the details of why the sequence is increasing and bounded by $5$). The book's answer is incorrect. Indeed, the book's answer doesn't even make sense, since it is easy to see that every term of the sequence is $\geq 3$ and so its limit, if it exists, must be $\geq 3$.

Recursive Sequence $a_n = \frac{1}{2} (a_{n-1} + 5) $

3 Answers3