I asked myself this question when I was a young boy playing around with the calculator.
Today, I think I know the answer, but I'm not sure whether I'd be able to explain it to a child or layman playing around with a calculator.
Hence I'm interested in answers suitable for a person that, say, knows what the square root of a square number is, but doesn't know about sequences, functions, convergence and the like.
Here is how I had justified it to myself when I was a kid (I was convinced :-))
If $x > 1$ then $\sqrt x > 1$ and $x > \sqrt x$.
So we keep reducing the number while still being $> 1$.
Also, we cannot end up at a number $>1$ as then taking the square root would reduce it.
If we do end up at $1$, we stay there. Since the calculator has a limited precision, we end up at $1$, and pretty quickly.
Of course, the assumption here is that we do end up somewhere :-) (Which seemed justified by the fact that the first non-zero digit after the decimal point always seemed to reduce)
Make a picture of the usual spiral converging to the fixed point, in the style of 
Where does this little obsession aparent on this site with 'layman' explanations? :P
NB. The picture comes from the Wikipedia page on fixed points.
Later. To make the picture it is better to use the cosine (so you do not even have to make the picture because that is what's in the wikipedia page) mainly because the iteration is seen more clearly: for the square root, the sequence converges boringly and fast to be interesting.
PS. You can draw this kind of pictures, assuming you have acces to Mathematica, with the following code:
f[t_] := Cos[t];
g = Plot[{f[t], t}, {t, -\[Pi]/2, \[Pi]/2},
AspectRatio -> 1, PlotStyle -> {Thick}, Epilog ->
Module[{pts = NestList[f, .1, 10]},
{
Thin, PointSize[0.015],
Line@ Flatten[Map[{#, {#[[2]], #[[2]]}} &, Partition[pts, 2, 1], 1], 1],
Red, Point[Partition[pts, 2, 1]]
}
]
]
If they know about logarithms, try this:
Dualizing reduces it to: repeatedly squaring $1+\epsilon$ goes to $\infty$. But that's clear by the Binomial theorem.
Namely: given any positive $\;\epsilon, \;$ we can force $\;\;\; 2^n\epsilon > x \;\;$ by choosing $\: n \:$ large enough.
Therefore we have that $\;\;\; (1+\epsilon)^{2^n} \ge 1+2^n \epsilon > x \ge 1\quad$ by the Binomial Theorem.
So, taking $\;2^n\:$'th roots: $\;\;\; 1+\epsilon \;\ge\; x^{1/2^n} \;\ge\; 1. \;\;$ Hence $\; x^{1/2^n}\to 1\;$ as $\;n\to\infty$
A nice series of solutions has already been given. It's hard to improve on any of them. But because this is an elementary question, it deserves an elementary answer. (Although "elementary" is subjective, being able to punch buttons on a calculator requires little mathematical sophistication, so we should attempt to minimize the formality and maximize the intuition in the explanation.)
When you begin with a value x on the calculator with x > 1, note that its square root lies between 1 and the midpoint of the interval [1, x].
(Proofs: The midpoint is (x+1)/2. Because ((x+1)/2)^2 - x = ((x-1)/2)^2 >= 0, the midpoint is no greater than the root of x. Non-algebraic version: draw graphs of the relations x = y^2 and y = (1+x)/2 on the same plot and note that the latter never falls below the former.)
It follows immediately (by induction if you want to be formal) that the iterated root, although never falling below 1, decreases faster than the iterated average with 1, which obviously (on geometric or arithmetic grounds) converges to 1.
The case of 0 < x < 1 is reduced to the case 1/x > 1 because Sqrt(1/x) = 1/Sqrt(x).
I think a better question is to analyze how the roots of a number X approach 1, depending on X. I.e. xa ~ 1 + a(lnX). Not only does this introduce the log, it gives a natural derivation of e which is easy to remember. I never understood what was "natural" about the natural log until I was an undergraduate, and I think the real value of this sequence is the way it leads so memorably and naturally to the derivation of e.
It's easy to see why you arrive at one from repeatedly taking square roots (as moron answered), since the sequence is strictly decreasing and bounded below by 1. I think a motivated person of almost any age can understand that, as long as it's explained slowly and clearly.
If $x>1$ then, since $x-1=(\sqrt{x}-1)(\sqrt{x}+1)$ and $\sqrt{x}>1$, so $(\sqrt{x}-1)/(x-1) =1/(\sqrt{x}+1) \lt 1/2$, so $\sqrt{x}$ is closer to $1$ than $x$ by a factor of at least $2$.
A similar argument holds when $0 < x < 1$.
For the sake of completeness, I will write down a rigorous explanation that is not intended for the layman.
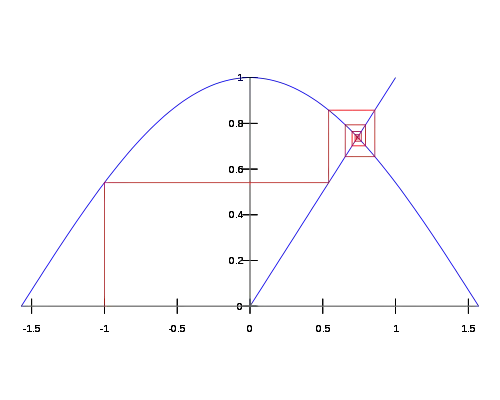
What is being observed is the following theorem: if $x\in(0,\infty)$, then the sequence $(a_n)$ given by $a_0=x$ and $a_{n+1}=\sqrt{a_n}$ converges to $1$.
Suppose that $x\in(0,1)$. Then, it is straightforward to prove by induction to prove that $(a_n)$ is increasing and bounded above, so $(a_n)$ is convergent (and it converges to its least upper bound). Writing $l$ for $\lim_{n\to\infty}a_n$, we have $$ l=\lim_{n\to\infty}a_{n+1}=\lim_{n\to\infty}\sqrt{a_n}=\sqrt{l} \, , $$ with the last equality being justified by the continuity of the square root function.
This means that, for each $x\in(0,1)$, either the sequence $(a_n)$ converges to $1$, or the sequence converges to $0$. But $0$ is not an upper bound of $(a_n)$, and it must be that, in each case, $l=1$. When $x\in[1,\infty)$, the argument is similar: $(a_n)$ is decreasing and bounded below, and so it converges to its greatest lower bound. That greatest lower bound must be $1$ rather than $0$, since it is provable that $1$ is a lower bound of $(a_n)$, and $1>0$.
This argument proves that $1$ is an attracting fixed point of the square root function: not only is $1$ a fixed point, there is a neighbourhood $N$ of $1$ such that if $x\in N$, then the sequence $x,\sqrt{x},\sqrt{\sqrt x},\dots$ converges to $1$. By contrast, $0$ is a fixed point of the square root, but not an attracting fixed point.
if(x == 0): sqrt(x) == 0
if(0 < x < 1): x < sqrt(x) < 1
if(x == 1): sqrt(x) == 1
if(1 < x ): 1 < sqrt(x) < x
Except for the cases x == 0 and x == 1, x != sqrt(x) so it must move, and it must move towards 1, so it will approach 1 to any accuracy you choose.
