Iteration for solving $x=g(x)$.

Question

$g(x) = \frac{x^2}{3}$

$P=3$

$p_0 = 3.5$

1) Graph $g(x)$, the line $y=x$, and the fixed point $P$ (done)

2) Using the given starting value $p_0$, compute $p_1$ and $p_2$ (the answer might be $p_1 = 4.083333,p_2 = 5.537869$)

Determine geometrically if fixed point iteration converges (answer: diverges)

We might decide this using the analogical graphing structure:

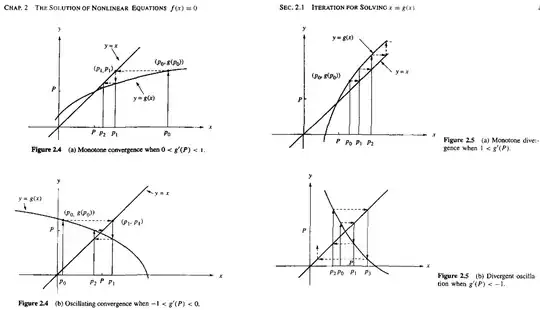
enter image description here

Please, help!

By the way, I got $p_2=5.557870...$. Looks like you copied a digit wrong. — Thomas Andrews, Feb 05 '13 at 18:25
I need to know how to get those answers . It has to deal with g'(P) = 2. From figure 2.5 it's monotone divergent as 1< g'(P). But I also need to find $p_1$, $p_2$
It is probably related to the formula $|P-p_n| \le K^n |P-p_0|$. — John Lennon, Feb 05 '13 at 18:29
the answer says, $p_2 = 5.537869$ However, they are not always exact, so yours is probably correct. — John Lennon, Feb 05 '13 at 18:31
Plugged it into a calculator. $p_1=g(p_0)$, $p_2=g(p_1)$.... — Thomas Andrews, Feb 05 '13 at 20:13
BTW the pictures in the post are taken from the book John H. Mathews, Kurtis D. Fink: Numerical methods using MATLAB. — Martin Sleziak, Aug 06 '16 at 13:57

score 3 · Accepted Answer · answered Feb 05 '13 at 18:30

3

Writing $g(x)=x\cdot \frac{x}{3}$, we see that if $x>3$ then $g(x)>x$ and if $0\leq x<3$, then $g(x)<x$. So what we see is that, unless $p_0=3$, $g(p_0),g(g(p_0)),...$ is going to get steadily further away from $3$.

answered Feb 05 '13 at 18:30

Thomas Andrews

177,126

I am also wondering how you get $p_1$, $p_2$. Thank you. – John Lennon Feb 05 '13 at 18:35

score 2 · Answer 2 · answered Feb 05 '13 at 18:39

Your graph should look like something like this:

enter image description here

If $p_0$ is a bit to the right of the fixed point $p=3$, we have $p_1 = g(p_0) > p_0$, so the iteration takes you farther away from the fixed point, and it diverges. Similarly if $p_0$ was a bit to the left of the fixed point $p=3$, you'd have $p_1 = g(p_0) < p_0$. In that case it would converge to the other other fixed point $0$.

Iteration for solving $x=g(x)$.

2 Answers2

Linked