How many ways are there to prove Cayley-Hamilton Theorem?

Question

I see many proofs for the Cayley-Hamilton Theorem in textbooks and net, so I want to know how many proofs are there for this important and applicable theorem?

Answer 1

My favorite : let $k$ be your ground field, and let $A = k[X_{ij}]_{1\leqslant i,j\leqslant n}$ be the ring of polynomials in $n^2$ indeterminates over $k$, and $K = Frac(A)$.

Then put $M = (X_{ij})_{ij}\in M_n(A)$ the "generic matrix".

For any $N=(a_{ij})_{ij}\in M_n(k)$, there is a unique $k$-algebra morphism $\varphi_N:A\to k$ defined by $\varphi(X_{ij}) = a_{ij}$ that satisfies $\varphi(M)=N$.

Then the characteristic polynomial of $M$ is separable (ie $M$ has $n$ distinct eingenvalues in an algebraic closure $\widetilde{K}$ of $K$). Indeed, otherwise its resultant $Res(\chi_M)$ is zero, so for any $N\in M_n(k)$, $Res(\chi_N) = Res(\chi_{\varphi_N(M)})= \varphi_N(Res(\chi_M)) = 0$, so no matrix $N\in M_n(k)$ would have distinct eigenvalues (but obviously some do, just take a diagonal matrix).

It's easy to show that matrices with separable characteristic polynomial satisfy Cayley-Hamilton (because they are diagonalizable in an algebraic closure), so $M$ satisfies Cayley-Hamilton.

Now for any $N\in M_n(k)$, $\chi_N(N) = \varphi_N(\chi_M(M)) = \varphi_N(0) = 0$.

Answer 2

Here is a neat proof from Qiaochu Yuan's answer to this question:

If $L$ is diagonalizable with eigenvalues $\lambda_1, \dots \lambda_n$, then it's clear that $(L - \lambda_1) \dots (L - \lambda_n) = 0$, which is the Cayley-Hamilton theorem for $L$. But the Cayley-Hamilton theorem is a "continuous" fact: for an $n \times n$ matrix it asserts that $n^2$ polynomial functions of the $n^2$ entries of $L$ vanish. And the diagonalizable matrices are dense (over $\mathbb{C}$). Hence we get Cayley-Hamilton in general.

Answer 3

One can prove this theorem by use of the fact that the matrix representation of all linear map on a complex vector space, is Triangularisable with respect to a basis $\{v_1,...,v_n\}$.

So if $T$ be a linear map there are $\{\lambda_1,...,\lambda_n\}$ s.t
$$T(v_1)=\lambda_1 v_1 $$ $$T(v_2)=a_{11} v_1+\lambda_2 v_2 $$ $$.$$ $$.$$ $$.$$ $$T(v_n)=a_{n1}v_1+a_{n2}v_2+...+\lambda_n v_n $$

And by computation we can find that the matrix $S=(T-\lambda_1)(T-\lambda_2)...(T-\lambda_n)$ vanishes all $v_i$, and so $S\equiv 0$.
For more details you can see Herstein's Topics in Algebra.

Answer 4

Here is a proof which doesn't assume that our field is algebraically closed (or involve passing to a field extension). For any square matrix $M$, let $c_M(t)$ be the characteristic polynomial of $M$. What we want to show is that $c_M(M)=0$.

Lemma 1: Let $A$ be an $n \times n$ matrix and suppose that there is a vector $v$ such that $v$, $Av$, $A^2 v$, ..., $A^{n-1} v$ is a basis of $k^n$. Then $c_A(A)=0$.

Proof: Since $v$, $Av$, $A^2 v$, ..., $A^{n-1} v$ is a basis, we have some linear relationship $A^n v + \sum_{j=0}^{n-1} f_j A^j v=0$. We set $f_n=1$ so we can write $$\sum_{j=0}^n f_j A^j v = 0 \quad (\ast).$$ Then, in the basis $v$, $Av$, $A^2 v$, ..., $A^{n-1} v$, the linear operator $A$ has matrix $$ \begin{bmatrix} 1&0&0&\cdots&0&-f_n \\ 0&1&0&\cdots&0&-f_{n-1} \\ 0&0&1&\cdots&0&-f_{n-2} \\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ 0&0&0&\cdots&1&-f_1 \\ \end{bmatrix}. $$ Using this basis, we compute that $c_A(t) = \sum f_j t^j$. Now, multipltying $(\ast)$ by $A^k$ on the left, we deduce that $$A^k \left( \sum f_j A^j \right) v = \left( \sum f_j A^{k+j} \right) v = \left( \sum f_j A^j \right) A^k v = c_A(A) A^k v = 0.$$ Thus, $c(A)$ kills each of the basis elements $v$, $Av$, $A^2 v$, ..., $A^{n-1} v$, and we deduce that $c_A(A)=0$. $\square$

Lemma 2: Suppose that $A$ is a matrix with block form $\left[ \begin{smallmatrix} X&Y \\ 0&Z \end{smallmatrix} \right]$ and that $c_X(X)=0$ and $c_Z(Z)=0$. Then $c_A(A)=0$.

Proof: The determinant of a block matrix is the product of the determinants of the diagonal blocks, so $c_A(t) = c_X(t) c_Z(t)$, so we have $$c_A(A) = c_X(A) c_Z(A) = \begin{bmatrix} c_X(X) & \ast \\ 0 & c_X(Z) \end{bmatrix} \begin{bmatrix} c_Z(X) & \ast \\ 0 & c_Z(Z) \end{bmatrix}$$ $$=\begin{bmatrix} 0 & \ast \\ 0 & c_X(Z) \end{bmatrix} \begin{bmatrix} c_Z(X) & \ast \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 0&0 \\ 0&0 \\ \end{bmatrix}. \qquad \square$$

Proof of the Cayley-Hamilton theorem: We induct on $\dim V$; if $\dim V=0$, the result is vacuously true.

Now, suppose $\dim V=n>0$ and choose a nonzero $v \in V$. Find the minimal $r$ such that there is a linear relation between $v$, $Av$, $A^2 v$, ..., $A^{r-1} v$, $A^r v$. Since $v \neq 0$, we have $r \geq 1$. If $r=n$, we are done by Lemma 1.

If not, complete $v$, $Av$, $A^2 v$, ..., $A^{r-1} v$ to a basis $v$, $Av$, $A^2 v$, ..., $A^{r-1} v$, $w_{r+1}$, $w_{r+2}$, $\dots$, $w_n$ of $k^n$. In this basis, $A$ has block form $\left[ \begin{smallmatrix} X&Y \\ 0&Z \end{smallmatrix} \right]$, with the $X$-block being $r \times r$ and the $Z$-block being $(n-r) \times (n-r)$. By induction, we have $c_X(X) = 0$ and $c_Z(Z)=0$, and we conclude by Lemma 2. $\square$

Answer 5

A few years ago I gave an "ugly" and long proof (more than 4 pages), which is purely computational.

Basically, I took an $n\times n$ matrix $A=(a_{i,j})_{i,j}$, where $a_{i,j}$ are variables. Then I wrote the characteristic polynomial as $P_A(X)=c_nX^n+\cdots +c_0$, where each $c_k$ is an explicit polynomial in the variables $a_{i,j}$. Then I wrote explicitly the $n^2$ entries of each $A^k$ with $0\leq k\leq n$ as polynomials in the variables $a_{i,j}$. Finally, I proved that each of the $n^2$ entries of $P_A(A)=c_nA^n+\cdots +c_0I_n$ is $0$. It's just playing with sums of monomials and proving that all of them reduce in the end.

You can find the proof in the 3-4/2014 issue of Gazeta Matematica, Seria A, pages 32-36. Available online at this address: https://ssmr.ro/gazeta/gma/2014/gma3-4-2014-continut.pdf

Answer 6

The Cayley-Hamilton Theorem says 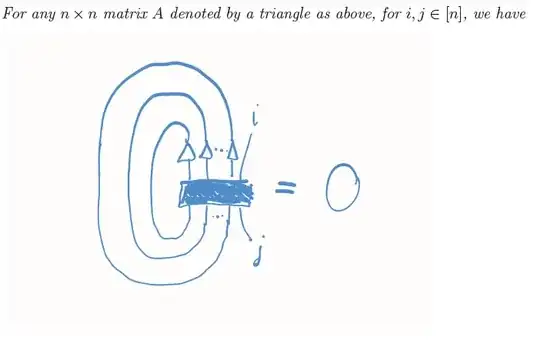where the dark box represents an antisymmetrizer of size $n+1$.

The proof of the theorem is a trivial application of the pigeonhole principle. What takes a bit more time and effort is to see that this is indeed the familiar Cayley-Hamilton Theorem. For more details, see Section 6.5 of the book by P. Cvitanović, Group theory. Birdtracks, Lie's, and exceptional groups. Princeton University Press, Princeton, NJ, 2008.

This point view was used by V. Lafforgue in his recent work https://arxiv.org/abs/1209.5352

Answer 7

[This is just a version of Sh.R’s answer above]

Consider ${ A \in \mathbb{C} ^{n \times n } }.$ By upper triangularization, there exists a basis ${ [P _1, \ldots, P _n] }$ such that $${ A [P _1, \ldots, P _n] = [P _1, \ldots, P _n] U }$$ and $${ U = \begin{pmatrix} \lambda _1 &* &* &\ldots &* \\ &\lambda _2 &* &\ldots &* \\ & &\ddots & &\vdots \\ & & &\lambda _{n-1} &* \\ & & & & \lambda _n \end{pmatrix} }.$$

Writing ${ P = [P _1, \ldots, P _n ] },$ since $${ \det(tI - A) = \det(P ^{-1} (tI - A) P) = \det(tI - P ^{-1} A P) }$$ we have polynomial $${ f(t) = \det(tI - A) = \det(tI - U) = (t - \lambda _1) \ldots (t - \lambda _n) }.$$

We are interested in the matrix $${ f(A) = P f(P ^{-1} A P) P ^{-1} = P f(U) P ^{-1} . }$$

We can show matrix ${ f(U) = 0 }$ (and hence ${ f(A) = 0 }$).

Thm: Let ${ U }$ be an upper triangular matrix $${ U = \begin{pmatrix} \lambda _1 &* &* &\ldots &* \\ &\lambda _2 &* &\ldots &* \\ & &\ddots & &\vdots \\ & & &\lambda _{n-1} &* \\ & & & & \lambda _n \end{pmatrix} }.$$ Then ${ f(U) = (U - \lambda _1 I) \ldots (U - \lambda _n I) = 0 }.$

Pf: We have ${ U = \begin{pmatrix} \lambda _1 &* &\ldots &* \\ 0& &\tilde{U} \end{pmatrix} }$ with submatrix ${ \tilde{U} = \begin{pmatrix} \lambda _2 &* &* &\ldots &* \\ &\ddots & & &\vdots \\ & & &\lambda _{n-1} &* \\ & & & & \lambda _n \end{pmatrix} }.$
By induction hypothesis, $${ (\tilde{U} - \lambda _2 I) \ldots (\tilde{U} - \lambda _n I) = 0 }.$$ Hence $${ (U - \lambda _2 I) \ldots (U - \lambda _n I) }$$ $${ \begin{align*} &= \begin{pmatrix} * &* &\ldots &* \\ 0& &\tilde{U} - \lambda _2 I \end{pmatrix} \ldots \begin{pmatrix} * &* &\ldots &* \\ 0& &\tilde{U} - \lambda _n I \end{pmatrix} \\ &= \begin{pmatrix} * &* &\ldots &* \\ 0 & &(\tilde{U} - \lambda _2 I) \ldots (\tilde{U} - \lambda _n I) \end{pmatrix} = \begin{pmatrix} * &* &\ldots &* \\ 0 & &0 & \end{pmatrix}. \end{align*}}$$ Hence $${ (U - \lambda _1 I) (U - \lambda _2 I) \ldots (U - \lambda _n I) }$$ $${ \begin{align*} &= \begin{pmatrix} 0 &* &\ldots &* \\ 0 & &\tilde{U}-\lambda _1 I & \end{pmatrix} \begin{pmatrix} * &* &\ldots &* \\ 0 & &0 & \end{pmatrix} = 0 , \end{align*} }$$ as needed.