Curve-fitting using circles

Question

I'm working for a firm, who can only use straight lines and (parts of) circles.

Now I would like to do the following: imagine a square of size $5\times5$. I would like to expand it with $2$ in the $x$-direction and $1$ in the $y$-direction. The expected result is a rectangle of size $7\times9$. Until here, everything is OK.

Now I would like the edges to be rounded, but as the length expanding is different in $x$ and $y$ direction, the rounding should be based on ellipses, not on circles, but I don't have ellipses to my disposal, so I'll need to approximate those ellipses using circular arcs.

I've been looking on the internet for articles about this matter (searching for splines, Bézier, interpolation, ...), but I don't find anything. I have tried myself to invent my own approximation using standard curvature calculations, but I don't find a way to glue the curvature circular arcs together.

Does somebody know a way to approximate ellipses using circular arcs?

Thanks
Dominique

Any sufficiently continuous curve can locally be approximated by a circle. — Wouter, Mar 02 '16 at 14:33
Engineeringwise, your problem declinates into some different mathematical approaches, depending on the actual constraints: are you going to cut, mill, draw the piece ? do you move $x-y$ with fixed diameter of the cutting edge, or ... ? — G Cab, Jan 11 '18 at 10:45

score 3 · Answer 1 · edited Jul 27 '21 at 18:23

Being given any prescribed ellipse curve, it is possible to find a parametric family of circles having this ellipse as its envelope (see figure 2 below). The more circles you take, the more precise you are.

How are these circles obtained? As an oblique projection of level sets of an ellipsoid (Figure 1) with equation:

$$\tag{1}x^2+y^2+\dfrac{z^2}{c^2}=1 \ \iff \ x^2+y^2=1-\dfrac{z^2}{c^2}$$

i.e., as circles of radius $r:=\sqrt{1-\tfrac{z^2}{c^2}}$.

These circles are parametrized by $z$ with parametric equations:

$$(C_z) \ \begin{cases} x=r \cos(u)+z\\y=r \sin(u) \end{cases} \ \ \text{for any } z \in [-c,c].$$

Here is a Matlab program that generates this family of circles (changing the value of parameter $c$ changes the eccentricity of the generated ellipse):

clear all;close all;axis equal;axis off;hold on
c=1;
u=0:0.01:2*pi;
for z=-c:0.1:c;
   r=sqrt(1-(z/c)^2);
   x=r*cos(u)+z;
   y=r*sin(u);
   plot(x,y);
end;

In fact there are two circles with radius 0, i.e., points that are the foci of this ellipse. This will become clearer with the following modification and its physical interpretation :

In fact, one can have more evenly spaced circles (it is in this way that Figure 2 has been generated) by setting $z=c \sin(t)$ for parameter $t \in [-\tfrac{\pi}{2},\tfrac{\pi}{2}]$. It means that the loop in the program above is to be replaced by :

for t=-pi/2:pi/24:pi/2;
   x=cos(t)*cos(u)+c*sin(t);
   y=cos(t)*sin(u);
   plot(x,y);
end;

A nice physical interpretation of this new family of circles is as sound waves propagation (see fig. 2) (http://www.math.ubc.ca/~cass/courses/m309-01a/dawson/index.html).

Remarks about machining concerns:

it is easy to retrieve the intersection points of successive circles where the tool must proceed to the next arc (dropping of course certain circles that remain interior to the elliptical envelope).
a better fit can be achieved by introducing tangents between the arcs. A supplementary benefit would be to obtain a smooth curve, but without continuity of the derivative.

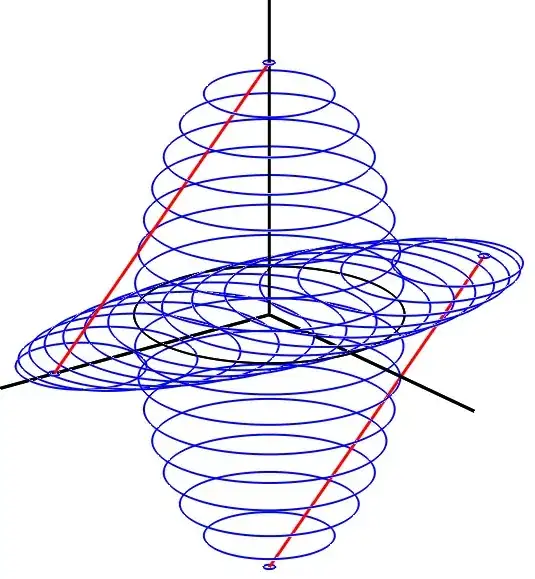
Fig. 1: Oblique (45°) projection on plane xOy of the level sets of the ellipsoid (called "prolate spheroid") with equation (1).

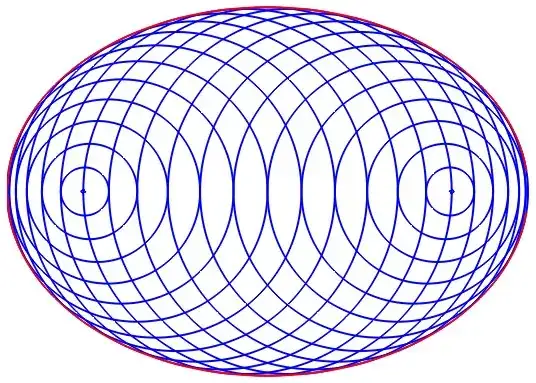
Fig. 2: Sound waves propagation interpretation: A sound emmitted from one of the foci of the ellipse is reflected on the ellipse and concentrated in the other focus.

score 3 · Answer 2 · answered Mar 02 '16 at 16:01

Here is an article that I used to implement a routine for converting Bézier curves to tangent arcs that may help you. It includes C++ code. Biarc Interpolation

If this doesn't qualify as an answer on this site, maybe someone could post the link as a comment instead and I will remove the answer.

bubba · Answer 3 · 2016-03-03T13:15:11.367

If you want to control the error in the approximation, then biarc interpolation/approximation is what you need, as indicated in the answer from @Paul H.

A biarc curve is usually constructed from two points and two tangent vectors. This actually leaves one degree of freedom unfixed, and there are several different ways to fix this. It can be shown that the "junction" where the two arcs meet lies somewhere on a certain circle, and you can choose where. See this paper for more than you probably want to know.

To get a good approximation, you'll probably have to use several biarc curves, strung end-to-end. Start out with the end-points and end-tangents of your quarter ellipse, and construct a single biarc. Calculate 10 or 15 points along the ellipse, and measure their distance to the biarc, to estimate the approximation error. If the error is too large, compute a point and tangent at some interior location on the ellipse, and approximate with two biarcs. Rinse and repeat until you have an approximation that's satisfactory. More details in this paper.

If you just want a simple approximation, and you don't care very much about the error, then there is a technique that draftsmen have used to draw ellipses for decades, sometimes called the "four center" method. See section 5.2.0 of this document., or this web page.

Curve-fitting using circles

3 Answers3

Linked