In page-10 of this pdf, a method to find envelope using circles is described. Is there a name for this method and what are sources to read more on it?
2 Answers
First of all, see this alternative document and its extension here with very sound explanations.
This method could be called "the wavefront method" or the "Huygens-Fresnel" method (as Snake707 has remarked) which is classical in optics. See for example here. See as well fig. 2 in this past answer of mine about sound envelopes.
Here is a way to interpret the issue in this case using the metaphor of fireworks.
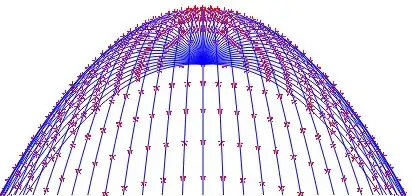
Imagine fireworks being ignited from a unique spot and sent in all directions. Let us assume that each individual rocket emits light all the time plus a more intense light at every tenth of second for example. I have seen such fireworks and it is striking to observe the formation of circles (observable due to persistence on light on our retina) as illustrated on the figure here (obtained by a quickly written Matlab simulation program), in perfect agreement with the figure in the document you give.
Edit: Starting from cinematic equations (1) and (2) in the document:
$$\begin{cases}x&=&vt \cos \theta \\ y&=&-\tfrac12gt^2+vt\sin \theta +h \end{cases}$$
that we can write:
$$\begin{cases}x&=&vt \cos \theta \\ y-(h-\tfrac12gt^2)&=&vt\sin \theta \end{cases}$$
if we square and add them, we get equation (8) giving the equation of the generic circle $(C_t)$, for a fixed value of $t$. Written it under the classical following form, where $(x_0,y_0)$ are the center's coordinates and $R$ the radius:
$$(x-x_t)^2 +(y-y_t)^2=R_t^2$$
we have: $$x_t=0, \ \ \ y_t=h-\tfrac12 gt^2, \ \ \ R_t=vt$$
The expression of $y_t$ shows that the center of $(C_t)$ is, right from the beginning, going down and down, crossing the $x$ axis for $t = \dfrac{2h}{g}$.
- 81,803
-
1If you could share a link to where I could read on more examples of the method then this would be a complete answer which I will accept – tryst with freedom Apr 01 '21 at 09:35
-
I just added 3 references. – Jean Marie Apr 01 '21 at 10:23
-
unrelated to main post but would be grateful if you could help, could you give a precise reason for why we account for the gravity lowering the center? Is it because it's an external effect? – tryst with freedom Apr 01 '21 at 17:31
-
Is it said like this in the text, and if this is so, on which page ? – Jean Marie Apr 01 '21 at 17:38
-
page-10 of linked PDF @Jean Marie – tryst with freedom Apr 01 '21 at 17:41
-
In my graphics (as in the graphics of the document), if I take back the realization as a set of little "fireworks rockets" launched not from the origin but from the summit of a pole, considering that any circle is the locus of the rockets at a same time, their center of gravity,, after having been well above this summit, begins by going down, and down, till it reaches the level of the ground. The center of gravity has no reasons to coincide with the center of the circle (it should be always above), but there is no doubt that they have both an ascending and descending phase. – Jean Marie Apr 01 '21 at 18:09
-
Let us continue this discussion in chat. – tryst with freedom Apr 01 '21 at 18:23
-
Ohh, apologies, still thank you for helping out! I'll check in the morning again @Jean Marie – tryst with freedom Apr 01 '21 at 18:48
-
I just added an "edit" to my answer. Is it the answer you were looking for ? – Jean Marie Apr 02 '21 at 08:43
-
1I'm trying to find an exact reason of why we must add $ -\frac{gt^2}{2}$ to the y coordinate of circle @Jean Marie – tryst with freedom Apr 02 '21 at 08:44
-
The reference document is well written but too "formula talkative": too much equations and too few text. This is often the case for projects' documents written by students. Compare with the expository style of this excellent document I just found using keywords "projectile trajectories shooting envelope circles". – Jean Marie Apr 02 '21 at 09:10
-
Thank you so much! I think this is was exactly what I was looking for and yes that was exactly the problem I felt when trying to read linked pdf. I can't follow the equations directly, I needed some explanation in english. – tryst with freedom Apr 02 '21 at 09:15
-
You might be interested by this generalization by the same author about ballistic (intercontinental) rocket trajectories. I have been working on this issue in the past: it is very nice, with parabolas plainly replaced by ellipses, etc. – Jean Marie Apr 02 '21 at 10:27