I like to think of helices on cylinders as images of lines under planar curling, so here's an approach incorporating that idea.
Imagine the circle rolling up a line drawn in the plane, with $P$ the point of tangency along the line and $Q$ a distinguished point on the circumference of the circle. (So, $Q$ traces out a cycloid in the plane.) Now, imagine the plane is made of thin paper, but the circle is made of stiff cardboard. If we curl the plane into a cylinder but the circle remains flat, the plane of the circle will be tangent to the cylinder along the (vertical) line passing through the point $P$. The point $P$ will follow a helix, and the point $Q$ --which lies in the plane of the circle-- traces out the helical cycloid in space. While the path that $P$ (and $Q$) takes is decidedly different after curling than before, the displacement vector between $P$ and $Q$ in the plane of the circle is the same throughout.
Before curling, if the circle of radius $r$ rolls along a horizontal track in the $uv$-plane, then we have $P=(r t, 0)$, and the point $Q$ traces out the standard cycloid:
$$\begin{align}
u &= r ( t - \sin t ) \\
v &= r ( 1 - \cos t )
\end{align}$$
The displacement vector from $P$ to $Q$ at time $t$ is given by
$$d := PQ = [m, n] = r[-\sin t, 1 - \cos t ] = - 2 r \sin\frac{t}{2} \; [\cos\frac{t}{2},-\sin\frac{t}{2}]$$
Rotating the plane through an angle, say, $\theta := \rm{atan\frac{c}{a}}$, and writing $b$ for $\sqrt{a^2+c^2}$, the circle's point of tangency along the tilted track is given by ...
$$P_2 = (r t \cos\theta,r t \sin\theta) = \left( \frac{r t a}{b}, \frac{r t c}{b}\right)$$
... and the displacement vector, $d_2$, to the point $Q_2$ tracing out the tilted cycloid is given by ...
$$\begin{align}
d_2 :&= [m \cos\theta - n \sin \theta, m \sin\theta + n \cos \theta ] \\
&= \frac{1}{b} [a m - c n, c m + a n] \\
&= -\frac{2r}{b}\sin\frac{t}{2}\left[\cos\left(\theta-\frac{t}{2}\right), \sin\left(\theta - \frac{t}{2} \right) \right] \\
\end{align}$$
Now the fun part: Curl the $(u,v)$-plane around a cylinder of radius $a$, such that the $uv$-origin aligns with the $xyz$-point $(a,0,0)$ and the $v$-axis runs parallel to the $z$ axis. The curled, tilted track will coincide with a helix. The horizontal distance travelled by $P_2$ in the plane becomes the length of horizontal circular arc travelled by $P_3$ around the cylinder; upon dividing by the radius, $a$, of the cylinder, this length becomes the angular "distance" --$s := \frac{rt}{b}$-- travelled by $P_3$; the vertical distances match. Therefore:
$$P_3 = \left(a\cos s, a\sin s, \frac{rtc}{b} \right)=(a\cos s,a\sin s,c s)$$
As for the displacement vector: The $u$ direction of the tangent plane coincides with the horizontal vector tangent to the cylinder at $P_3$; the $v$ direction coincides with the $z$ direction. Thus, the transformation from $uv$-coordinates to $xyz$-coordinates is given by
$$[1,0]\to[-\sin s, \cos s, 0]\hspace{0.5in}[0,1]\to[0,0,1]$$
The image, $d_3$, of the displacement vector $d_2$, then, is
$$d_3 = -\frac{2r}{b}\sin\frac{t}{2}\left[-\sin s \cos\left(\theta-\frac{t}{2}\right), \cos s \cos\left(\theta-\frac{t}{2}\right), \sin\left(\theta - \frac{t}{2} \right) \right] $$
and the path of $Q_3$, which traces the helical cycloid, is given by
$$
Q_3 = P_3 + d_3 = \left\{
\begin{align}
x &= a \cos s &+ \frac{2 r}{b} \sin s \sin\frac{bs}{2r} \cos\left(\theta-\frac{bs}{2r}\right)\\
y &= a \sin s &- \frac{2 r}{b} \cos s \sin\frac{bs}{2r} \cos\left(\theta-\frac{bs}{2r}\right)\\
z &= c s &- \frac{2 r}{b} \sin\frac{b s}{2r}\sin\left(\theta-\frac{bs}{2r}\right)
\end{align}
\right.
$$
Here's a picture with $a=c=1$ and $r=1/2$:
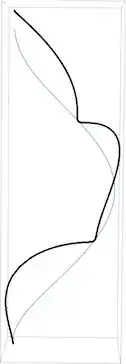
Note: The above does not simply curl the planar cycloid around the cylinder. Since
$$x^2 + y^2 = a^2 + \frac{4r^2}{b^2} \sin^2\frac{bs}{2r} \cos^2\left(\theta-\frac{bs}{2r}\right) \ge a^2$$
we see that most of the helical cycloid lies outside the surface of the cylinder.
