For an university assignment I have to visualize some curves in 3 dimensional space.
Until now I've implemented Bézier, helix and conical spiral.
Could you give me some advice about some famous curves in geometry history?
For an university assignment I have to visualize some curves in 3 dimensional space.
Until now I've implemented Bézier, helix and conical spiral.
Could you give me some advice about some famous curves in geometry history?
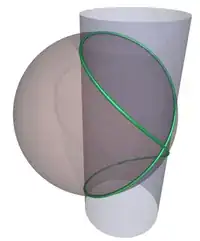
How about Viviani's curve? It is the intersection of a sphere with a cylinder. Viviani was a student (or disciple) of Gallileo.
Wikipedia has a beautiful image:
I'd mention the curve of Archytas, the space curve formed by the intersection of a horn torus and a cylinder:
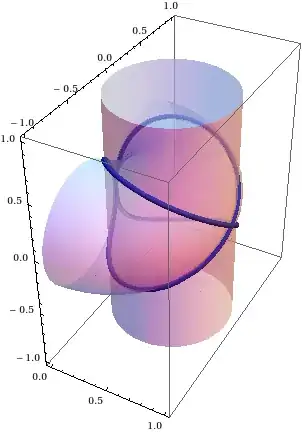
The parametric equations for the curve of Archytas are
$$\begin{align*}x&=\frac{\cos^4 t}{(1+\sin^2 t)^2}\\y&=\frac{\cos\,t\sin\,2t}{(1+\sin^2 t)^2}\\z&=\frac{\sin\,2t}{\sqrt 2(1+\sin^2 t)}\end{align*}$$
Archytas of Tarentum used this curve to help him solve the Delian problem.
Though is it is not 3D, the Clothoid or Cornu Spiral is an amazing curve. It surely can be made 3D by adding a simple extra parameter $z(t)=t$. It has infinite length but converges to two points in the plane. It has several applications in optics and road engineering, for example. An it looks quite nice:
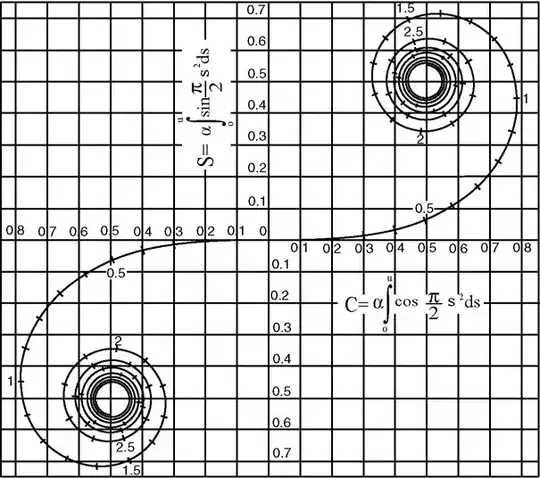
I found a 3D plot too:

Let $t \in [0,2\pi]$. And let $r(t)=\frac{1}{2-\sin (2t)}[\cos(3t),\sin(3t),\cos(2t)]$. Then $r(t)$ parametrizes a 3-dimensional curve with no three-tangent plane (I must admit I'm not sure of the English terminology here) - that is, every tangent plane of the curve meets the curve in no more than two points.
(I have no clue how to prove such things, however)
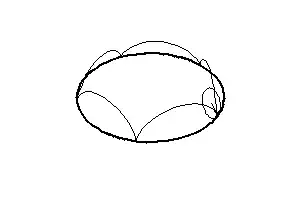
If I may be allowed to give another example, there is the spherical epitrochoid, the locus of a circle rolling on another circle. It was studied by Johann Bernoulli and Franz Reuleaux in the context of the kinematics of gear systems.
Letting $p$ be the radius of the fixed circle ("pitch circle"), $r$ the radius of the rolling circle, $hr$ the distance of the tracing point from the center of the rolling circle, and $\omega$ the inclination of the rolling circle from the x-y coordinate plane, the parametric equations for the spherical epitrochoid are:
$$\begin{align*}x&=(p+r\cos\;\omega)\cos\;t-h r\left(\cos\;\omega\cos\left(\frac{p}{r}t\right)\cos\;t-\sin\left(\frac{p}{r}t\right)\sin\;t\right)\\y&=(p+r \cos\;\omega)\sin\;t-h r\left(\cos\;\omega\cos\left(\frac{p}{r}t\right)\sin\;t+\sin\left(\frac{p}{r}t\right)\cos\;t\right)\\z&=r\sin\;\omega\left(1-h\cos\left(\frac{p}{r}t\right)\right)\end{align*}$$
Here is the case $p=1$, $r=\frac15$, $h=1$, $\omega=\frac{2\pi}{3}$:
Here is the case $p=1$, $r=\frac15$, $h=1$, $\omega=\frac{\pi}{6}$:

wow! thanks all, everyone got very interesting answer i've found also slinky that is quite funny cause it is also a toy