0

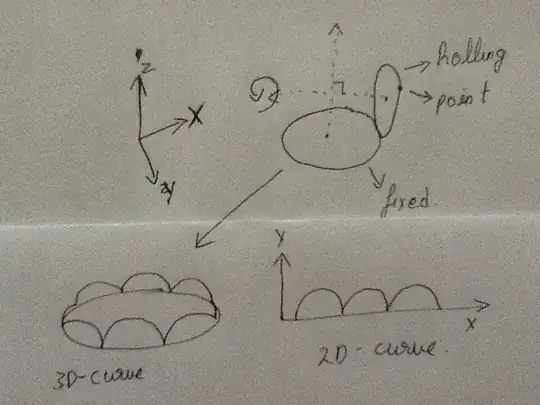
I'm trying to find out 3D parametric equations for a cycloid. I know that a cycloid is a 2D curve that is generated by a point on a rolling circle.

But my circle is rolling around another circle, and both of these circle axes are perpendicular to each other. The second circle is stationary and the first circle with the point is rolling around the fixed one. I need to get an equation for the curve generated by the point.

Please avoid vectors.

The 2D parametric equation for the cycloid is

$$\begin{align*}x(t)&=rt-r\sin(t)\\ y(t)&=r-r\cos(t)\end{align*}$$

where $r$ is the radius.

I need this

$x(u,v)=?\\ y(u,v)=?\\ z(u,v)=?$

I have been trying to get this for a year for my project. 3D equations are tough. Any help would be appreciated. thanks

Picture to show my problem picture

Glorfindel
  • 3,955
Zany
  • 163
  • 6
  • can you draw a figure to indicate the relative orientation of the fixed circle and the rolling circle? – mike Jun 18 '14 at 13:00
  • I have updated the post with an image link let me know if you need more details thanks for the help – Zany Jun 18 '14 at 13:45

2 Answers2

1

This previous answer displays the explicit parametric equations for the spherical epitrochoid, which I will reproduce here for completeness:

$$\begin{align*}x&=(p+r\cos\;\omega)\cos\;t-h r\left(\cos\;\omega\cos\left(\frac{p}{r}t\right)\cos\;t-\sin\left(\frac{p}{r}t\right)\sin\;t\right)\\y&=(p+r \cos\;\omega)\sin\;t-h r\left(\cos\;\omega\cos\left(\frac{p}{r}t\right)\sin\;t+\sin\left(\frac{p}{r}t\right)\cos\;t\right)\\z&=(r\sin\;\omega)\left(1-h\cos\left(\frac{p}{r}t\right)\right)\end{align*}$$

where $p$ is the radius of the fixed circle ("pitch circle"), $r$ is the radius of the rolling circle, $\omega$ gives the tilt of the rolling circle (for the OP's particular case, $\omega=\frac{\pi}{2}$), and $h$ gives the fraction of the distance from the rolling circle's center (in the cycloidal case the OP is interested in, $h=1$).

Community
  • 1
J. M. ain't a mathematician
  • 75,051
1

From the two-dimensional parametrization, we simply have $$\begin{align*} x(t) &= R \cos \bigl( \tfrac{r}{R}(t - \sin t) \bigr), \\ y(t) &= R \sin \bigl( \tfrac{r}{R}(t - \sin t) \bigr), \\ z(t) &= r - r \cos t. \end{align*}$$ Suitable choices for $r$ and $R$ will yield a closed curve, in which case the appropriate range for $t$ is $t \in [0, 2\pi R/r).$

heropup
  • 135,869
  • I want to graph this curve but in my graphing application it has two parameters u and v how do you suppose I should modify the above equation I am just an ordinary math guy dealing at most with simple curves like cycloid please help me out – Zany Jun 18 '14 at 14:02
  • With a mapping $f : \mathbb R^2 \to \mathbb R^3$, you will get a surface rather than a curve in Euclidean 3-space. You can make a minor modification to get something like a "ribbon," e.g., $$\begin{align} x(u,v) &= v R \cos ( r(u \sin u)/R ), \ y(u,v) &= v R \sin (r(u - \sin u)/R ), \ z(u,v) &= r - r \cos u. \end{align}$$ Here, the range of $v$ will be around $1$; e.g., $v \in [0.99, 1.01]$ will make a close approximation to a line. – heropup Jun 18 '14 at 14:10
  • You may set $R=5r$ and $u=v=t$, then $X(u,v)=X(t,t)=x(t)$, $Y(u,v)=Y(t,t)=y(t)$, $Z(u,v)=Z(t,t)=z(t)$. – mike Jun 18 '14 at 14:12
  • can someone please explain how the above equation was obtained. – Zany Nov 02 '14 at 10:39