4

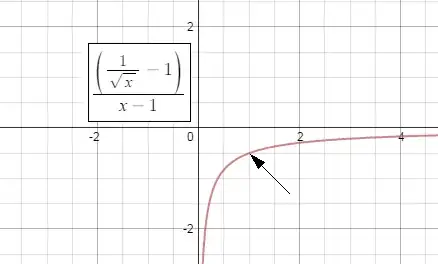
I posted a solution here with an illustration (see below) and commented that the function was discontinuous at $x=1$, where it is undefined. Someone told me, no, it is undefined but continuous.

Now I'm confused.

I would have thought that the point $(1, -1/2)$ in the graph below should be designated with a hollow point (a point that isn't filled in) to demonstrate that that point is not actually on the graph. Furthermore, I thought that this hole would constitute a discontinuity.

If I need to be set straight here, could someone please help me out?

undefined point

Community
  • 1
MathAdam
  • 3,309
  • 1
    For sure,it should be marked with a circle because the point x=1 is not in the domain. – Koro Sep 12 '15 at 06:07
  • I added the clarification that someone had told me that it is undefined at this point, but continuous. Wouldn't the circle be a discontinuity? – MathAdam Sep 12 '15 at 06:09
  • There is more to that,even the graph that you plotted is incorrect because at x=1 ,function is undefined so a hole should be there on the intersection of the line x=1 and the graph that u have drawn. – Koro Sep 12 '15 at 06:12
  • 1
    It has to be a discontinuity.If it's not (suppose) then for continuity we must have value of function at a point= limit at that point. So in the present case, limit exists but value doesn't so function is discontinuous at x=1. – Koro Sep 12 '15 at 06:14
  • @kilimanjaro - That's what I thought. Thanks. – MathAdam Sep 12 '15 at 06:15
  • Welcome! Someone probably confused you. – Koro Sep 12 '15 at 06:16
  • 1
    What the person could have meant was that the function itself is continuous which simply means that it's continuous in all points where it's defined – Alice Ryhl Sep 12 '15 at 06:44
  • 2
    Your function is not defined at $x=1$. Thus it does not make sense to say that $f$ is continuous (or discontinuous) at $x=1$. –  Sep 12 '15 at 06:47
  • @KristofferRyhl or what the person could have meant was that the limit exists at $1$. a lot of students (incorrectly) think that if the limit of a function exists at $c$ then it's continuous at $c$. – chharvey Sep 12 '15 at 16:00

3 Answers3

11

If a function is undefined at a point, then you can't speak of it being either continuous or discontinuous there. Those terms are only defined for points in the domain of the function. Stein and Barcellos, Calculus and Analytic Geometry, 5th Edition (Sec. 2.8):

According to this definition any polynomial is continuous. So is each of the basic trigonometric functions, including $y = \tan x$... You may be tempted to say, 'But $\tan x$ blows up at $π/2$ and I have to lift my pencil off the paper to draw the graph.' However, $π/2$ is not in the domain of the tangent function... If $a$ is not in the domain of $f$, we do not define either continuity or discontinuity there.

Daniel R. Collins
  • 8,380
9

A function from a set $A$ to a set $B$ is a certain subset of their Cartesian product. Any property of a function must therefore refer to its defining data. As such, continuity or lack thereof can only be determined in the domain of the function.

This is NOT pedantry. The function $f$ defined on $\mathbb{R}\setminus \{0\}$ which takes the value $1$ for $x>0$ and $-1$ for $x<0$ is a continuous function. There is no "in its domain" qualifier. It is a continuous function, period. In the OP's example, the function is perfectly continuous and even has a continuous extension to the entire real line.

Edit: now that the other answer is edited, the clarification is no longer necessary.

Edit 2: Justify downvotes.

guest
  • 4,772
  • Your argument reminds me of the point made here about limits. The post makes a similar point about restricting the test to the domain of the function.http://math.stackexchange.com/a/1429451/266049 – MathAdam Sep 12 '15 at 14:09
  • I found your aside about the extension helpful as well. – MathAdam Sep 12 '15 at 14:11
  • Thanks much. I love this stuff. We're such geeks. ;) – MathAdam Sep 12 '15 at 15:53
  • It sounds like you are saying we can speak of a function's being discontinuous at a point outside its domain. Wouldn't that be trivial? What I find more interesting is where a function is discontinuous within its domain. – MathAdam Sep 12 '15 at 16:11
  • @AdamHrankowski Yes, your textbook definition allows to say a function is not continuous (I don't want to say is discontinuous, it looks like a positive statement and adds to confusion!) at a point $c$ outside its domain. Of course generally we only care about what happens in the domain, but there are cases, like yours, where the function can be extended outside of its domain, and then these extensions become interesting. In ODE for instance, we can sometimes push a solution outside the domain it is originally defined, so those points we found uninteresting before become interesting now :) – guest Sep 12 '15 at 16:19
  • @AdamHrankowski so in your example, by your textbook definition $f$ is a continuous function which is not continuous at $1$ and which has a continuous extension at $1$ :D Oh dear... – guest Sep 12 '15 at 16:21
  • @guest , please see , I want more discussion http://math.stackexchange.com/questions/1495246/if-a-function-is-not-continuous-then-is-it-possible-for-bounded-function-in-give – Mithlesh Upadhyay Oct 24 '15 at 13:55
4

Excerpt from my answer to this question:

The term continuous function is defined with respect to its domain. Therefore it is crucial to specify the domain of a function, if we want to analyse the function with respect to continuity. Outside of the domain of a function this function is not continuous, since it's not even defined there.

Note that when we talk about discontinuities of a one variable function we classify them as either being a removable discontinuity, a jump discontinuity or an essential resp. infinite discontinuity. The key point here is, that each of these discontinuities is defined with respect to the domain of $f$. We conclude, discontinuities are defined solely within the domain of $f$.

Informally: The domain and codomain specify where the function lives and we can't say anything about the function outside of its region of existence.

Community
  • 1
Markus Scheuer
  • 108,315
  • I am confused. Let $f(x) = \frac{1}{x}$. As far as I know there must exist a corresponding value in the range of the function for all $x$ in its domain so that we can call it a function. So for $f(x)$ to be a function, its domain $(D)$ must be $\mathbb{R}\setminus {0}$. So $f(x)$ is a continuous function. So can we say that there isn't a function (not piecewise) that is discontinuous at a point (obviously) in its domain? – Lars Smith Jan 01 '21 at 13:19
  • Thank you, I will try to explain myself with an example: If we were asked to find points where $f$'s discontinuous, we would say that the function is continuous everywhere, right? Or any other function like let's say $g(x) = \frac{x-2}{x-2}$. This is also continuous everywhere. This is because we should look for discontinuities in the domain of the function. And since a function needs to be defined at all points of its domain, I think (and am asking if this is true) there is no any function (not including pieceone functions) that is discontinuous at any point of its domain. – Lars Smith Jan 01 '21 at 16:26
  • The reason I think so is probably because for a function that's not piecewise, most of the discontinuities I saw were because of the zero at the denominator. It often makes an infinite discontinuity or a removable discontinuity. But now I see since the domain of the function doesn't involve the value that makes the denominator $0$ (it wouldn't be a function if it does, because all $x$ doesn't have a value in the range), we can't count them as discontinuous points, and so such functions don't have discontinuities. I hope this was a better explanation of myself. – Lars Smith Jan 01 '21 at 16:27
  • 1
    @LarsSmith: There are other types of functions with interesting properties regarding discontinuities. Consider for instance: $f:[0,1]\to[0,1]$, $f(x)=\begin{cases}x&x\in\mathbb{Q}\1-x&x\in\mathbb{R}\setminus\mathbb{Q}\end{cases}$. Here $f$ is only continuous at $x=\frac{1}{2}$, although it takes each value between $f(0)=0$ and $f(1)=1$. Note that also the domain is crucial for deciding continuity of a function at a point. For instance a function is always continuous at isolated points which might not be that intuitive. – Markus Scheuer Jan 01 '21 at 17:18
  • 1
    In fact we have always to check if left-hand limit is equal to right-hand limit is equal to the function at the specific point under consideration (and which of these exist with respect to the given domain). – Markus Scheuer Jan 01 '21 at 17:18