16

Possible Duplicate:
Proof for an integral involving sinc function
How do I show that $\int_{-\infty}^\infty \frac{ \sin x \sin nx}{x^2} \ dx = \pi$?

$\int_{-\infty}^{\infty}\sin^2(x)/x^2=\pi$ according to wolfram alpha. That is such a beautiful result! But how do I calculate this integral by hand?

Thanks in advance.

Community
  • 1
ftiaronsem
  • 1,089
  • 1
    I added an answer there using Siminore's suggestion below to integrate by parts. – joriki May 06 '12 at 11:58
  • If you are familiar with Fourier Analysis, you can calculate the inverse of $\frac{\sin x}{x}$, then use Parseval-Plancherel equality to get the result. – zy_ May 06 '12 at 14:02
  • The answer may be found by using complex analysis, specifically the residue theorem. A full deriviation may be found here. I know of an easy way to derive this result using real analysis alone. – Nathaniel Bubis May 06 '12 at 11:17

4 Answers4

49

An easy way:

$$I(a)=\int_{-\infty}^{\infty}\frac{\sin^2(ax)dx}{x^2}$$

$$\implies \frac{dI}{da}=\int_{-\infty}^{\infty}\frac{\sin(2ax)dx}{x}=\pi$$

$$\implies I(a)=\pi a+const$$

$$\implies I(a)=\pi a$$ because $I(0)=0$

Atharva Pathak
  • 3
Martin Gales
  • 6,878
31

First we split $\sin^2(x)=\frac{(1-e^{2ix})+(1-e^{-2ix})}{4}$. To avoid the pole at $x=0$, drop the path of integration a bit below the real line (this function has no poles and it vanishes at infinity, so this is okay).

Next, let $\gamma^+$ be the path below the real axis, then circling back in a semi-circular path counterclockwise around the upper half-plane; and let $\gamma^-$ be the path below the real axis, then circling back in a semi-circular path clockwise around the lower half-plane.

$\hspace{4cm}$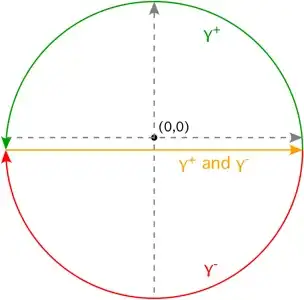enter image description here

Note that $\gamma^+$ circles the pole at $x=0$ of $\frac{(1-e^{2ix})}{4x^2}$ and $\gamma^-$ misses the pole at $x=0$ of $\frac{(1-e^{-2ix})}{4x^2}$.

Therefore, $$ \begin{align} \int_{-\infty}^\infty\frac{\sin^2(x)}{x^2}\mathrm{d}x &=\int_{-\infty-i}^{\infty-i}\frac{1-\cos(2x)}{2x^2}\mathrm{d}x\\ &=\int_{-\infty-i}^{\infty-i}\frac{(1-e^{2ix})+(1-e^{-2ix})}{4x^2}\mathrm{d}x\\ &=\color{green}{\int_{\gamma^+}\frac{(1-e^{2ix})}{4x^2}\mathrm{d}x}+\color{red}{\int_{\gamma^-}\frac{(1-e^{-2ix})}{4x^2}\mathrm{d}x}\\ &=\color{green}{2\pi i\frac{-2i}{4}}+\color{red}{0}\\ &=\pi \end{align} $$

robjohn
  • 345,667
  • If by $\int _{-\infty -i}^{\infty -i}$ you mean the integral over the line $y=-1,$ how do we know the integral over this line is equal to the integral over $\mathbb{R}$? – The Substitute Apr 15 '15 at 08:18
  • 3
    Because $\frac{\sin^2(x)}{x^2}$ has no singularities and tends to $0$ along the ends of the long rectangle $[-R,R]\cup\color{#C00000}{[R,R-i]}\cup[R-i,-R-i]\cup\color{#C00000}{[-R-i,-R]}$. The integral along that contour tends to the difference of the two integrals as $R\to\infty$. (That was the intended meaning of the parenthetical comment.) – robjohn Apr 15 '15 at 08:24
  • For a Fourier analytic approach to this integral, see this answer. – robjohn Nov 29 '16 at 01:08
  • Would the downvoter care to explain if something is wrong? I don't see anything wrong, so I would appreciate knowing if there is some error. – robjohn Dec 04 '17 at 13:45
  • Just to clarify a point if I may, the original function $\frac{\sin^2{x}}{x^2}$ has no pole at 0. It is an analytic function on the entire complex plane. This justifies the shifting trick. But $sin^2{z}$ is not easy to control as $R\rightarrow0$. Hence the answer separates $\frac{\sin^2{x}}{x^2}$ into three parts all which have singularity at zero. The upper and lower are picked in a way that controls the growth of the numerator. – Shuheng Zheng Dec 12 '21 at 04:15
  • $\frac{\sin^2(x)}{x^2}$ is an entire function which decays to $0$ for bounded $\operatorname{Im}(x)$ and $|\operatorname{Re}(x)|\to\infty$. Thus, $$\int_{-\infty}^\infty\frac{\sin^2(x)}{x^2},\mathrm{d}x=\int_{-\infty-i}^{\infty-i}\frac{\sin^2(x)}{x^2},\mathrm{d}x$$ Then we break $\frac{\sin^2(x)}{x^2}$ into two parts: $\frac{1-e^{2ix}}{4x^2}$ and $\frac{1-e^{-2ix}}{4x^2}$, integrating each along contours where $x$ avoids $0$ and the integrals along the semicircles vanishes. – robjohn Dec 12 '21 at 08:09
13

Use Parseval theorem $\int_{-\infty}^{\infty}dx |f(x)|^{2}= \int_{-\infty}^{\infty}du|F(u)|^{2} $

the Fourier inverse transform of $ \frac{\sin(x)}{x} $ is an step function (window function )

Sine of the Time
  • 4,931
Jose Garcia
  • 8,506
5

This is, for example, Exercise 2 of chapter 11 of the book Complex analysis by Bak and Newman. The hint is: integrate $$\frac{e^{2iz}-1-2iz}{z^2}$$ around a large semi-circle.

Siminore
  • 35,136