8

I came across a previous awesome question about the visualization of the distribution of polynomial roots and tried to do a simpler version applied to the set of real roots of quadratic equations $ax^2+bx+c=0$.

To visualize the pattern of the relationship between the set of real roots, the algorithm in Python calculates the roots $x_1,x_2$ only for the specific values of the intervals $a \in [-a_i,a_i]$, $b \in [-b_i,b_i]$, $c \in [-c_i,c_i]$, $a,b,c \in \Bbb N$. If the limits $a_i,b_i,c_i$ are very big, the set of roots is very dense and it is very difficult to visualize the emerging pattern.

These are three methods I have tried to visualize the relationship between the roots $x_1,x_2$, my questions are at the end of them.

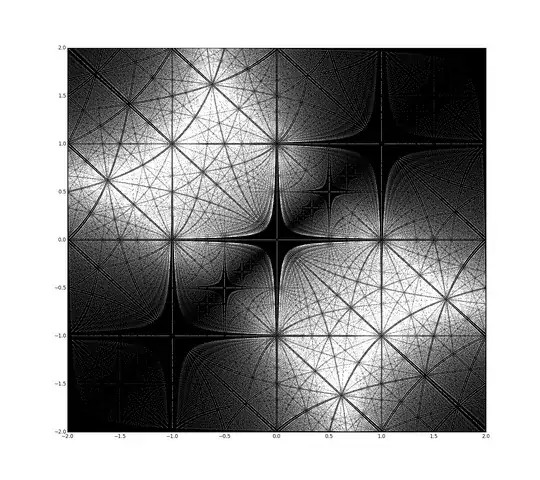
  1. Cartesian coordinates $(x,y)=(x_1,x_2)$. E.g. $a_i,b_i,c_i=75$: enter image description here

  2. Polar coordinates $(\theta, r)=(x_1,x_2)$. E.g. $a_i,b_i,c_i=75$: enter image description here Due to the symmetries the opposite patterns $(x,y)=(x_2,x_1)$ and $(\theta, r)=(x_2,x_1)$ are similar.

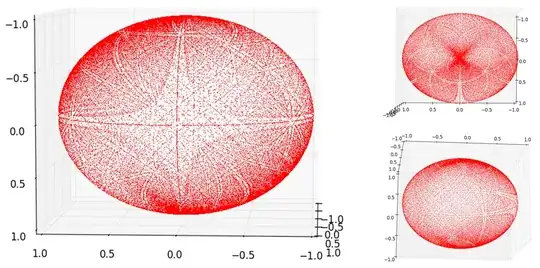
  3. Spherical coordinates $(\theta, \phi, r)=(x_1,x_2,1)$. E.g. $a_i,b_i,c_i=25$: enter image description here

So basically there seems to be a pattern in the relationship between both real roots that can be visualized.

I would like to ask the following questions:

  1. What methods are known to visualize patterns in the set of real roots of quadratic equations?

  2. Are there references to papers or studies about this subject?

Thank you!

UPDATE 2015/08/31

As requested, this is the pattern shown by the Cartesian coordinates example that was included above (1), when $a_i,b_i,c_i=575$ and using only the square roots of the prime numbers of those intervals, $\sqrt{a} \ / a \in [-a_i,a_i]$, $\sqrt{b} \ / b \in [-b_i,b_i]$, $\sqrt{c} \ / c \in [-c_i,c_i]$. This will show the pattern of the roots only for a) $a,b,c$ irrationals (because the square roots of prime numbers are irrational numbers) and still constrained to b) $x_1,x_2 \in \Bbb R$:

enter image description here

UPDATE 2015/09/02

Due to the size of the images I can not add some other animations I have prepared: In this link you will find the graphs of the quadratic complex roots, and also the graphs of the complex and real roots of cubic equations.

Community
  • 1
iadvd
  • 8,875
  • 2
    I believe coloring the density of roots at a point $(x_1,x_2)$ would be the best way to see the complex nature of the plane. Once again, Multi-Fractals come to mind. In addition, what happens when a,b, & c are rational rather than just natural numbers? For instance, the behavior of $p=0$, $k$ from your other recent question changes a lot if $k$ can be a real number. Having said that, I still find your visualization to be interesting. These problems show the underlying complexity inherent to numbers and that's definitely interesting. – Zach466920 Aug 28 '15 at 18:45
  • 2
    @Zach466920 thank you for the comment! when I add 100 real points between each natural number, this is $a+(0.01..0.99)$, same for each $b,c$, the result is the same regarding the patterns (as far as I am avoiding complex roots). The problem is that the density of the set of roots grows up very much, so it is difficult to see the patterns, everything gets white very soon for the same $a,b,c$ intervals. I did not try other combinations yet.I would like to see is how does look like a 3-dimensional projection of the five dimensional set of $(a,b,c,x_1,x_2)$, in polar coordinates seems interesting. – iadvd Aug 29 '15 at 11:31
  • 2
    Cool, great stuff. You might be able to color the density by counting points, within a radius $r$, surrounding an $(x_i,y_i)$ and then color coding. I don't know how computationally difficult that is though. – Zach466920 Aug 29 '15 at 14:38
  • 2
    @Zach466920 hi, I have added an example of the Cartesian coordinates applied only to irrationals, to make the trick I am expanding the initial intervals and taking only the prime numbers of those intervals, and then making their square roots (because the square roots of prime numbers are irrationals). This requires a bigger interval because there will be less good candidates inside due to the constraints. I will try to make the density plotting you suggest on your first comment, but it might take a time. As you guessed, the pattern is quite different but the shapes found are similar! :) – iadvd Aug 31 '15 at 01:10

1 Answers1

0

It has been a long time since I asked this question. I will keep it open some more days before closing, hoping someone else will be able to add more options of visualization.

Recently I have been able to learn another interesting methodology that can be applied to the visualization of the roots. We will define the tuples $(a,b,c,x_1),(a,b,c,x_2)$ as points of a $4$-dimensional space, projected into the $3$-dimensional space. The methodology is explained in this question.

Basically, we allocate the points inside a $4D$ tesseract whose center will be the origin of coordinates in the $4$-dimensional space and the reference of the position of the points in the internal space of the tesseract, and then the tesseract and its content is projected into $3D$. The example below shows every real root for $a,b,c \in [-10,10] (a,b,c \in \Bbb Z$):

enter image description here

And below there is a zoom showing only the root tuples. As it can be seen, the pattern generated by the set of tuples shows interesting symmetries in the $4D$ space that can be observed in the $3D$ projection of the set of points (kind of mesmerizing!). The movement is required because to be able to visualize a complete $4D$ object through its projection, we need to rotate around one of the $4D$ axis. By doing so, it is possible to see the $3D$ "shadow" of the positions of the points in the original $4$-dimensional space:

enter image description here

Community
  • 1
iadvd
  • 8,875