How can I visualize a four-dimensional point inside a Schlegel diagram of a tesseract?

Question

I would like to draw a Schlegel diagram of a tesseract to visualize via a Cartesian coordinate system inside the tesseract the symmetry of some four-dimensional points located in a range of integer values no longer than the half of the length of the side of the tesseract. (The questions are at the end of the explanation)

My idea is as follows:

For instance in two dimensions, it is possible to visualize two-dimensional points $(x_1,x_2)$ inside a square whose side length is for instance $s$, where $| x_1 |,|x_2| \le \frac{s}{2}$ if the center of the Cartesian system is located in the center of the rectangle. In the same fashion, is is possible to do the same inside a cube for three-dimensional points $(x_1,x_2,x_3)$, locating the center of the Cartesian system in the exact center of the cube, keeping the same restriction for the values of the coefficients of the points (smaller than half the length of the side of any face of the cube.
I want to apply that idea for a set of four-dimensional points $(x_1,x_2,x_3,x_4)$ in the Schlegel diagram of a tesseract. But in this case I am not sure how to visualize a given point $(x_1,x_2,x_3,x_4)$. My guessing is something like this:

In a static image of the tesseract my intuition is that I should be able to visualize three coefficients of a given point $(x_1,x_2,x_3,x_4)$ for instance let us say for this example that they are $(x_1,x_2,x_3)$ (if the belong to the current position of visualization of the tesseract), but not very sure where should be located the fourth one (always assuming that it should be visible in the current position of visualization of the tesseract).

I would like to ask the following questions:

Is it possible to visualize four-dimensional points in a Schlegel diagram of a tesseract? Is there a known technique to do it correctly?

In the example above I have assumed that in a static view of the Schlegel diagram of the tesseract I can visualize three dimensions of a given point, for instance $x_1,x_2$ and $x_3$. Is that intuition wrong? Where should I plot/locate/visualize the remaining fourth dimension, $x_4$? Is it possible in a static image, or the diagram must be shown in movement so all the dimensions of each point are visualized depending on the "rotation" though the dimensions of the tesseract?

Is this kind of approach in use for visualization of fourth-dimensional problems in some field of Mathematics? Are there online tools (initially I did not find one) to make this kind of visualization?

Any hints are very welcomed, thank you!

UPDATE: I have found a very related question here.

I have started to find some clues: (1) https://en.wikipedia.org/wiki/Rotations_in_4-dimensional_Euclidean_space and (2) http://www.math.harvard.edu/archive/21b_fall_03/4dcube/ — iadvd, Feb 02 '17 at 03:23
My understanding of a Schlegel diagram is that it show points that are not in the interior of the polytope (i.e., all the points in a Schlegel diagram are on a facet of the polytope). A hypercube diagram shows 8 3-cubes; all points in the facets and interiors of these 3-cubes can be pointed to. Points in the interior of the hypercube aren't on the diagram. Also, the outermost facet is turned inside out; its interior points are on the 'outside'. This is analogous to the 2-D Schlegel diagram of a 3-cube. — Dan Moore, Feb 09 '17 at 17:34
@DanMoore thanks for the feedback! you are right, as I also confirmed in the answer below, written language sometimes is not perfect, trying to express ideas.The diagram as you say shows the projection of the surface of the tesseract, not the internal points, so my first attempt, shown in the question, was wrong. For that purpose, as per the answer, first project the surface of the tesseract via a Schlegel diagram, and then using the same projection rules, project a $4D$ point that is located inside the tesseract. That makes the visualization possible. — iadvd, Feb 09 '17 at 23:37

score 3 · Accepted Answer · edited Apr 13 '17 at 12:21

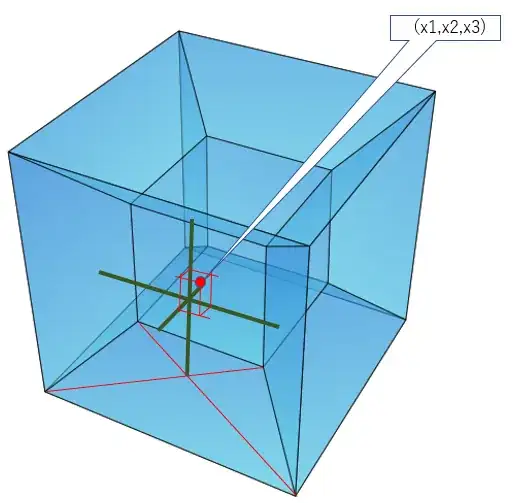
Well, gathering the information regarding the basic theory here and the nice explanation here regarding the projection, I was able to build my own version of the tesseract, and yes it is possible to show a point inside the tesseract, and I was wrong in the assumptions I made regarding the methodology applied to visualize the 4D point. Basically, if we want to show a point inside the tesseract, we need to project the tesseract first, and then project the desired point as well, following the same projection rules.

The definition of the tesseract (credits to draks...)

The tesseract is a four dimensional cube. It has 16 edge points $v=(a,b,c,d)$, with $a,b,c,d$ either equal to $+1$ or $-1$. Two points are connected, if their distance is $2$. Given a projection $P(x,y,z,w)=(x,y,z)$ from four dimensional space to three dimensional space, we can visualize the cube as an object in familiar space. The effect of a linear transformation like a rotation $$ R(t)=\pmatrix{1&0&0&0\\0&1&0&0&\\0&0&\cos(t)&\sin(t)\\0&0&-\sin(t)&\cos(t)} $$ in $4D$ space can be visualized in $3D$ by viewing the points $v(t) = P R(t) v$ in $\mathbb R^3$.

The definition of the projection (credits to Andrew D. Hwang)

$$ P(x, y, z, w) = \frac{h}{h - w}(x, y, z). $$

And finally, the definition of the distance between two four-dimensional points is calculated as follows (this is used to show the edges of the tesseract properly, making lines between the correct projected vertices):

$$d=\sqrt{(x_0-x'_0)^2+(x_1-x'_1)^2+(x_2-x'_2)^2+(x_3-x'_3)^2}$$

I have prepared a Python code snippet that creates the frames (jpg) of an animation of a tesseract including an internal point. In this case, the length of the edge is $1000$ so the distance between the vertices is not $2$, but $1000$. For the projection I have used a light source located at three times the length of the edge, this is $h=3000$. Finally, I have applied a rotation as defined above. The star is marking the location of the point $(\frac{3}{4} \cdot \frac{1000}{2}, \frac{3}{4} \cdot \frac{1000}{2}, \frac{3}{4} \cdot \frac{1000}{2}, \frac{3}{4} \cdot \frac{1000}{2})$ while we rotate the tesseract. Be aware that the position of the camera in the animation is lateral. The typical location of the camera is from above, which is the usual "square inside a square" view. But for visualization purposes (we want to see clearly the movement of the projection of the point due to the rotation of the tesseract) the camera in this case was located in a lateral position. Please use and modify it freely (for instance instead of one point it is possible to show a set of points and verify if there is symmetry, etc.):

from math import pi, sin , cos, sqrt
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D

edge_length=1000
edge_half_length= int(edge_length/2)

lotuples=[]
list_of_loxt_lists=[]
list_of_loyt_lists=[]
list_of_lozt_lists=[]

rotation_accuracy=100
filled_once=False
for ratio in range(0,rotation_accuracy):
    angle= ((2*pi)*ratio)/rotation_accuracy
    loxt=[]
    loyt=[]
    lozt=[]

    #t=edge_half_length (positive)
    a=-edge_half_length
    b=edge_half_length
    ret0=-edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=-edge_half_length
    ret0=-edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=edge_half_length
    ret0=-edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=-edge_half_length
    ret0=-edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=edge_half_length
    ret0=edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=-edge_half_length
    ret0=edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=edge_half_length
    ret0=edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=-edge_half_length
    ret0=edge_half_length
    ret1=edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    #t=-edge_half_length (negative)
    a=-edge_half_length
    b=edge_half_length
    ret0=-edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=-edge_half_length
    ret0=-edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=edge_half_length
    ret0=-edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=-edge_half_length
    ret0=-edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=edge_half_length
    ret0=edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=edge_half_length
    b=-edge_half_length
    ret0=edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=edge_half_length
    ret0=edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])

    a=-edge_half_length
    b=-edge_half_length
    ret0=edge_half_length
    ret1=-edge_half_length
    finala=a
    finalb=b
    finalret0=(ret0*cos(angle))+(ret1*sin(angle))
    finalret1=(ret0*(-sin(angle)))+(ret1*cos(angle))    

    light_projection_factor = ((edge_length*3)/((edge_length*3)-(finalret1)))
    loxt.append(light_projection_factor*finala)
    loyt.append(light_projection_factor*finalb)
    lozt.append(light_projection_factor*finalret0)
    if filled_once==False:
        lotuples.append([a,b,ret0,ret1])
        filled_once=True

    list_of_loxt_lists.append(loxt)
    list_of_loyt_lists.append(loyt)
    list_of_lozt_lists.append(lozt)

list_of_loxi_lists=[]
list_of_loyi_lists=[]
list_of_lozi_lists=[]

list_of_loxi_lists_axis=[]
list_of_loyi_lists_axis=[]
list_of_lozi_lists_axis=[]

for ratio in range(0,rotation_accuracy):
    angle= ((2*pi)*ratio)/rotation_accuracy
    loxi=[]
    loyi=[]
    lozi=[]

    finala=int((3/4)*edge_half_length)
    finalb=int((3/4)*edge_half_length)
    finalret0=(int((3/4)*edge_half_length)*cos(angle))+(int((3/4)*edge_half_length)*sin(angle))
    finalret1=(int((3/4)*edge_half_length)*(-sin(angle)))+(int((3/4)*edge_half_length)*cos(angle))

    light_projection_factor = ((edge_length*3)/((edge_length*3)-finalret1))
    loxi.append(light_projection_factor*finala)
    loyi.append(light_projection_factor*finalb)
    lozi.append(light_projection_factor*finalret0)

    list_of_loxi_lists.append(loxi)
    list_of_loyi_lists.append(loyi)
    list_of_lozi_lists.append(lozi)

    # Show projection of refence axes BEGIN
    loxi=[]
    loyi=[]
    lozi=[]

    finala_axis=finala
    finalb_axis=0
    finalret0_axis=0
    finalret1_axis=0

    light_projection_factor = ((edge_length*3)/((edge_length*3)-finalret1_axis))
    loxi.append(light_projection_factor*finala_axis)
    loyi.append(light_projection_factor*finalb_axis)
    lozi.append(light_projection_factor*finalret0_axis)

    finala_axis=0
    finalb_axis=finalb
    finalret0_axis=0
    finalret1_axis=0

    light_projection_factor = ((edge_length*3)/((edge_length*3)-finalret1_axis))
    loxi.append(light_projection_factor*finala_axis)
    loyi.append(light_projection_factor*finalb_axis)
    lozi.append(light_projection_factor*finalret0_axis)

    finala_axis=0
    finalb_axis=0
    finalret0_axis=finalret0
    finalret1_axis=0

    light_projection_factor = ((edge_length*3)/((edge_length*3)-finalret1_axis))
    loxi.append(light_projection_factor*finala_axis)
    loyi.append(light_projection_factor*finalb_axis)
    lozi.append(light_projection_factor*finalret0_axis)

    finala_axis=0
    finalb_axis=0
    finalret0_axis=0
    finalret1_axis=finalret1

    light_projection_factor = ((edge_length*3)/((edge_length*3)-finalret1_axis))
    loxi.append(light_projection_factor*finala_axis)
    loyi.append(light_projection_factor*finalb_axis)
    lozi.append(light_projection_factor*finalret0_axis)

    list_of_loxi_lists_axis.append(loxi)
    list_of_loyi_lists_axis.append(loyi)
    list_of_lozi_lists_axis.append(lozi)
    # Show projection of refence axes END

for ratio in range(0,rotation_accuracy):    
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    ax.view_init(elev=17., azim=-152)   

    for i in range(0,len(lotuples)):
        for j in range(i+1,len(lotuples)):
            distance = int(sqrt(((lotuples[i][0]-lotuples[j][0])**2)+((lotuples[i][1]-lotuples[j][1])**2)+((lotuples[i][2]-lotuples[j][2])**2)+((lotuples[i][3]-lotuples[j][3])**2)))
            if distance<=edge_length:
                ax.plot([list_of_loxt_lists[ratio][i],list_of_loxt_lists[ratio][j]],[list_of_loyt_lists[ratio][i],list_of_loyt_lists[ratio][j]],[list_of_lozt_lists[ratio][i],list_of_lozt_lists[ratio][j]],"r")


        ax.plot([-edge_length],[edge_length],[-edge_length],"w")
        ax.plot([-edge_length],[-edge_length],[-edge_length],"w")
        ax.plot([edge_length],[edge_length],[-edge_length],"w")
        ax.plot([edge_length],[-edge_length],[-edge_length],"w")
        ax.plot([edge_length],[edge_length],[edge_length],"w")
        ax.plot([edge_length],[-edge_length],[edge_length],"w")
        ax.plot([-edge_length],[edge_length],[edge_length],"w")
        ax.plot([-edge_length],[-edge_length],[edge_length],"w")

    ax.plot([list_of_loxi_lists[ratio][0]], [list_of_loyi_lists[ratio][0]], [list_of_lozi_lists[ratio][0]], "r*")

    #projection of refence axes around the point    
    ax.plot([0,list_of_loxi_lists_axis[ratio][0]],[0,list_of_loyi_lists_axis[ratio][0]],[0,list_of_lozi_lists[ratio][0]],"b")
    ax.plot([0,list_of_loxi_lists_axis[ratio][1]],[0,list_of_loyi_lists_axis[ratio][1]],[0,list_of_lozi_lists_axis[ratio][1]],"b")
    ax.plot([0,list_of_loxi_lists_axis[ratio][2]],[0,list_of_loyi_lists_axis[ratio][2]],[0,list_of_lozi_lists_axis[ratio][2]],"b")
    ax.plot([0,list_of_loxi_lists_axis[ratio][3]],[0,list_of_loyi_lists_axis[ratio][3]],[0,list_of_lozi_lists_axis[ratio][3]],"b")

    ax.dist=8
    mpl.pyplot.savefig("tesseract_movie_"+str(ratio)+".png")
    print("End ratio "+str(ratio))

(The animated gif was generated joining the jpg files with VirtualDub).

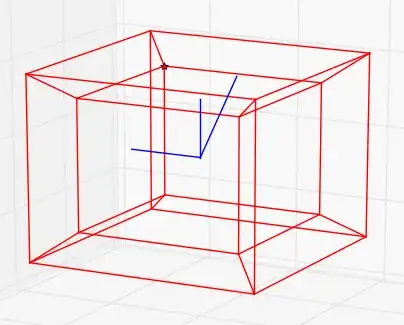
UPDATE 2017/02/06: I have included both in the image and the Python code in blue color the reference axes of the point (the projection of the $(x_0,0,0,0),(0,x_1,0,0),(0,0,x_2,0),(0,0,0,x_3)$ points and the reference axes generated with them).

The reason of this question was being able to visualize possible symmetries of $4$-tuples in a four-dimensional Euclidean space: http://math.stackexchange.com/questions/2131551/visualizing-4-tuples-a-b-x-y-of-the-extended-euclidean-algorithm-in-a-four-d — iadvd, Feb 06 '17 at 09:27

How can I visualize a four-dimensional point inside a Schlegel diagram of a tesseract?

1 Answers1

Linked