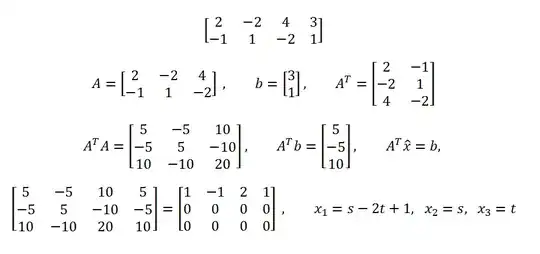I'm doing problems from old exams, and my solutions don't add up with the professor's solution. The problem is as followed: Find all least squares solutions of the linear system. I checked my calculations are correct, I checked with my TI-82 STATS calculator and used the correct formulas. Can you check if this is correct or not?
Modestly generalize the problem to consider underdetermined matrices of rank one.
We are given the matrix $\mathbf{A}\in\mathbb{R}^{2\times 3}$ and the data vector $b\in\mathbb{R}^{2\times 1}_{1}$ $$ \mathbf{A} = % \left[ \begin{array}{rrr} 2 & -2 & 4 \\ -1 & 1 & -2 \\ \end{array} \right], \quad % b = \left[ \begin{array}{c} 3 \\ 1 \end{array} \right] % $$ and the goal is to find the set least squares minimizers for $$ \mathbf{A} x = b.$$
The matrix $\mathbf{A}$ has $m=2$ rows, $n=3$ columns, and rank $\rho=1$. (There a few ways to resolve the rank. For example, notice that the two rows are linearly dependent.)
The set of least squares minimizers is defined as $$ x_{LS} = \left\{ x \in \mathbb{R}^{3} \colon \lVert \mathbf{A} x_{LS} - b\rVert_{2}^{2} \text{ is minimized} \right\}.\tag{1}$$
The Fundamental Theorem of Linear Algebra provides fundamental insight. A matrix $\mathbf{A} \in \mathbb{C}^{m\times n}_{\rho}$ induces for fundamental subspaces: $$ \begin{align} % \mathbf{C}^{n} = \color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)} \oplus \color{red}{\mathcal{N} \left( \mathbf{A} \right)} \\ % \mathbf{C}^{m} = \color{blue}{\mathcal{R} \left( \mathbf{A} \right)} \oplus \color{red} {\mathcal{N} \left( \mathbf{A}^{*} \right)} % \end{align} $$ (Blue denotes vectors in a $\color{blue}{range}$ space, red denotes vectors in a $\color{red}{null}$ space.)
Focus on the structure of the domain space. Because $\rho<n$, the null space is nontrivial: $$ \color{red}{\mathcal{N} \left( \mathbf{A} \right)} \ne \left\{ \mathbf{0} \right\} $$
Examination of the target matrix reveals some salient facts.
The two rows of $\mathbf{A}$ are linearly dependent: $$ \mathbf{A}_{1:*} = -2 \mathbf{A}_{2:*}.$$
The corresponding range space is then $$ \color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)} = \text{span} \left\{ \color{blue}{\left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right]} \right\} \tag{2}$$
The rank plus nullity theorem, indicates that $\color{red}{\mathcal{N} \left( \mathbf{A} \right)}$ will be spanned by two vectors.
The general solution will then contain a particular solution and a homogeneous solution: $$ x_{LS} = \color{blue}{x_{p}} + \color{red}{x_{h}}\tag{3}$$
The range space for the domain is $$ \color{blue}{\mathcal{R} \left( \mathbf{A} \right)} = \text{span} \left\{ \color{blue}{\left[ \begin{array}{r} 2 \\ -1 \end{array} \right]} \right\} \tag{4}$$
Because $\color{blue}{x_{p}} \in \color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)} $, we must have $$ \color{blue}{x_{p}} = \alpha \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right] } $$ with $\alpha\in\mathbb{R}$. Finding the particular solution boilds down to solving for $\alpha$.
Solve for $\alpha$
Use the solution definition in $(1)$ to compute $\alpha$. First, compute the residual error vector: $$ r(\alpha x) = \mathbf{A} (\alpha x) - b = \left[ \begin{array}{r} 12 \alpha - 3 \\ -6\alpha - 1 \end{array} \right] .$$ The total error is then $$ r(\alpha x)\cdot r(\alpha x) = 180\alpha^{2} - 60\alpha +10.$$ Minimize the total error by minimizing this function with respect to $\alpha.$ Find the zero values of the first derivative. $$ D_{\alpha} \left(180\alpha^{2} - 60\alpha +10 \right) = 0 \quad \implies \quad \alpha = \frac{1}{6}$$ Therefore the particular solution is $$ \color{blue}{x_{p}} = \frac{1}{6} \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right] }$$ (The least total error is $ 180\cdot\tfrac{1}{36} - 60\cdot\tfrac{1}{6} + 10 = 5.)$
We can resolve the null space by Intelligent Guessing. We are looking for two linearly independent vectors orthogonal to $\color{blue}{x_{p}}$. Try these shapes for the null space vectors: $$ \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right]} \cdot \color{red}{ \left[ \begin{array}{c} * \\ 0 \\ * \end{array} \right]} =\mathbf{0}, \qquad \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right]} \cdot \color{red}{ \left[ \begin{array}{c} * \\ * \\ 0 \end{array} \right]} =\mathbf{0}. $$ Two such choices are $$ \color{red}{v_{1}} = \color{red}{ \left[ \begin{array}{r} -2 \\ 0 \\ 1 \end{array} \right]}, \qquad \color{red}{v_{2}} = \color{red}{ \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right]}. $$ We have resolved the null space $$ \color{red}{\mathcal{N} \left( \mathbf{A} \right)} = \text{span} \left\{ \color{red}{v_{1}}, \color{red}{v_{2}} \right\} = \text{span} \left\{ \color{red}{ \left[ \begin{array}{r} -2 \\ 0 \\ 1 \end{array} \right]}, \color{red}{ \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right]} \right\}.$$ Homogeneous solutions will have the form $$ \color{red}{x_{h}} = \beta \color{red}{v_{1}} + \gamma \color{red}{v_{2}}. $$ where the constants $\beta$ and $\gamma$ are arbitrary.
The final solution is $$ \boxed{ x_{LS} = \color{blue}{x_{p}} + \color{red}{x_{h}} = \frac{1}{6} \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right] } + \beta \color{red}{ \left[ \begin{array}{r} -2 \\ 0 \\ 1 \end{array} \right]} + \gamma \color{red}{ \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right]}} $$ (You can verify that $\lVert \mathbf{A} x_{LS} - b\rVert_{2}^{2} = 5$.)
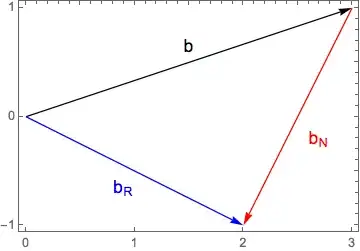
Because of the simplicity of the problem, it's easy to find the solution using projections. The trick is to resolve the data vector in range and null space components: $$ b = \color{blue}{b_{\mathcal{R}}} + \color{red}{b_{\mathcal{N}}}, $$ as seen in the following plot.
The vector $\color{blue}{b_{\mathcal{R}}}$ is projection of the data vector $b$ onto $\color{blue}{\mathcal{R}(\mathbf{A})}$. Pick a vector in the span, $$ \color{blue}{s} = \color{blue}{\left[ \begin{array}{r} 2 \\ -1 \end{array} \right]} $$ Compute the solution vector $$ \color{blue}{b_{\mathcal{R}}} = b \cdot \frac{\color{blue}{s}}{\lVert \color{blue}{s} \rVert} = \color{blue}{ \left[ \begin{array}{r} 2 \\ -1 \end{array} \right]} $$
With a data vector in the range space, the linear system is now consistent and can be solved with Gaussian-Jordan Elimination. $$ \begin{array}{ccc} \left[ \begin{array}{c|c} \mathbf{A} & \color{blue}{b_{\mathcal{R}}} \end{array} \right] & \to & \left[ \begin{array}{c|c} \mathbf{E_{A}} & R \end{array} \right] \\ \left[ \begin{array}{rrr|r} 2 & -2 & 4 & 2 \\ -1 & 1 & -2 & -1\\ \end{array} \right] & \to & \left[ \begin{array}{rrr|r} 1 & -1 & 2 & 1 \\ 0 & 0 & 0 & 0\\ \end{array} \right] \end{array} $$
The interpretation of the reduced matrix $\mathbf{E_{A}}$ is $$ x - y + 2z = 1. $$ To match the convention posed in the question, let $$ y = s, \quad z = t$$ to recover $$ x = s -2t + 1, \qquad s,t \in \mathbb{R}. $$ The least squares minimizes are the set $$ \boxed{ x_{LS} = \left[ \begin{array}{c} s - 2t + 1 \\ s \\ t \end{array} \right]}. $$ This represents the complete set of minimizers without resolving the range and null space components $\color{blue}{x_{p}} + \color{red}{x_{h}}.$
To connect the pieces, note that the values $s=-\tfrac{1}{6}$, $t=\tfrac{1}{3}$ produce $\color{blue}{x_{p}}$.
The normal equations will not produce a particular solution, but they will provide the set of least squares minimizers.
The product matrix is singular: $$ \begin{array}{ccc} \mathbf{A}^{*}\mathbf{A} x & = & \mathbf{A}^{*} b \\ \left[ \begin{array}{rrr} 5 & -5 & 10 \\ -5 & 5 & -10 \\ 10 & -10 & 20 \\ \end{array} \right] & = & \left[ \begin{array}{rrr|r} 5 \\ -5 \\ 10 \end{array} \right] \end{array} $$ Because rank$\left(\mathbf{A}\right) = 1$, the product matrix is also rank 1 and offers no inverse. The usual solution path $$ \color{blue}{x_{p}} = \left( \mathbf{A}^{*}\mathbf{A}\right)^{-1} \mathbf{A}^{*} b $$ is not available.
However, Gauss-Jordan elimination of the normal equations produces $$ \begin{array}{ccc} \left[ \begin{array}{c|c} \mathbf{A}^{*}\mathbf{A} & \mathbf{A}^{*} b \end{array} \right] & \to & \left[ \begin{array}{c|c} \mathbf{E_{A}} & R \end{array} \right] \\ \left[ \begin{array}{rrr|r} 5 & -5 & 10 & 5 \\ -5 & 5 & -10 & -5 \\ 10 & -10 & 20 & -10 \\ \end{array} \right] & \to & \left[ \begin{array}{rrr|r} 1 & -1 & 2 & 1 \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{array} \right] \end{array} $$ This is the same result from the previous solution.
The SVD will provide the pseudoinverse matrix needed by $\color(blue){x_{p}}$ and the null space projector for $\color(red){x_{h}}$.
For derivations, refer to How does the SVD solve the least squares problem?.
The general solution for the least squares problem in $(1)$ is $$ x_{LS} = \color{blue}{x_{p}} + \color{red}{x_{h}} = \underbrace{\mathbf{A}^{\dagger}b\vphantom{\big|}}_{\color{blue}{x_{p}}} + \underbrace{\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger} \mathbf{A}\right) y}_{\color{red}{x_{h}}}, \qquad y\in\mathbb{R}^{n} $$
The form of the singular value decomposition for this rank deficient problem is $$ \begin{align} \mathbf{A} &= \mathbf{U} \, \Sigma \, \mathbf{V}^{*} = % U \left[ \begin{array}{cc} \color{blue}{\mathbf{U}_{\mathcal{R}(\mathbf{A})}} & \color{red}{\mathbf{U}_{\mathcal{N}(\mathbf{A}^{*})}} \end{array} \right] % Sigma \left[ \begin{array}{cc} \mathbf{S} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array} \right] % V \left[ \begin{array}{l} \color{blue}{\mathbf{V}_{\mathcal{R}(\mathbf{A}^{*})}^{*}} \\ \color{red}{\mathbf{V}_{\mathcal{N}(\mathbf{A})}^{*}} \end{array} \right] \end{align} $$
The corresponding Moore-Penrose pseudoinverse matrix is $$ \begin{align} %% \mathbf{A}^{\dagger} &= \mathbf{V} \, \Sigma^{\dagger} \, \mathbf{U}^{*} = % U \left[ \begin{array}{cc} \color{blue}{\mathbf{V}_{\mathcal{R}(\mathbf{A}^{*})}} & \color{red}{\mathbf{V}_{\mathcal{N}(\mathbf{A})}} \end{array} \right] % Sigma \left[ \begin{array}{cc} \mathbf{S}^{-1} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array} \right] % V \left[ \begin{array}{l} \color{blue}{\mathbf{U}_{\mathcal{R}(\mathbf{A})}^{*}} \\ \color{red}{\mathbf{U}_{\mathcal{N}(\mathbf{A}^{*})}^{*}} \end{array} \right] \end{align} $$
Computational details can be found in Computing the SVD, and examples in Calculating SVD by hand: resolving sign ambiguities in the range vectors., and, Need to multiply by -1 for a SVD to work?.
Singular value spectrum The first step is to compute the singular values, which are the square roots of the ordered, non-zero, eigenvalues to the product matrix: $$\mathbf{A}\mathbf{A}^{*} = 6 \left[ \begin{array}{rr} 4 & -2 \\ -2 & 1 \\ \end{array} \right].$$ Pulling out the scaling factor of $6$ is not required, it's a personal peccadillo to simply hand calculations. Proceeding, the characteristic polynomial for the scaled eigenvalues $\Lambda$ is $$ p(\Lambda) = \det \left[ \begin{array}{rr} 4-\Lambda & -2 \\ -2 & 1-\Lambda \\ \end{array} \right] = \Lambda(\Lambda - 5) $$ The scaled and ordered eigenvalue spectrum is $$ \Lambda \left( \mathbf{A}\mathbf{A}^{*} \right) = \left\{ 5, 0\right\} $$ Restore the original scale of the eigenvalues using $\lambda = 6 \Lambda$, and take the square root: $$ \sigma = \sqrt{\lambda} = \sqrt{30}. $$
Resolve$\ \color{blue}{\mathbf{V}_{\mathcal{R}}}$
As there is but one vector in the domain, $$ \color{blue}{\mathbf{V_{\mathcal{R}}}} = \frac{1}{6} \color{blue}{\left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right]} $$
Resolve$\ \color{blue}{\mathbf{U_{\mathcal{R}}}}$
The final step is $$ \color{blue}{\mathbf{U_{\mathcal{R}}}} = \frac{1}{\sigma}\mathbf{A} \color{blue}{\mathbf{V}_{\mathcal{R}}} = \frac{1}{\sqrt{5}} \color{blue}{\left[ \begin{array}{r} -2 \\ 1 \end{array} \right]} $$
Using the thin SVD, the pseudoinverse matrix is $$ \mathbf{A}^{\dagger} = \frac{1}{30} \left[ \begin{array}{r} 2 & -1\\ -2 & 1\\ 4 & -2 \end{array} \right]. $$
The particular solution is the least squares solution of least norm and is computed using the pseudoinverse matrix: $$\color{blue}{x_{p}} = \mathbf{A}^{\dagger} b = \frac{1}{6} \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right] }, $$ as expected.
Assemble the projector onto $\ \color{red}{\mathcal{N} \left( \mathbf{A} \right)}$
The homogeneous term is handled by the projector onto $\color{red}{\mathcal{N} \left( \mathbf{A} \right)} $. Start with the projector onto the range space $\color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)}$: $$ \mathbf{P}_{\color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)}} = \frac{1}{6} \left[ \begin{array}{rrc} 1 & -1 & 2 \\ -1 & 1 & 2 \\ 2 & -2 & 4 \\ \end{array} \right] $$ The projector needed for the least squares solution is the projector onto the orthogonal complement of $\color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)}$: the projector onto the null space $\color{red}{\mathcal{N} \left( \mathbf{A} \right)}$. This projector is $$ \mathbf{P}_{\color{red}{\mathcal{N} \left( \mathbf{A} \right)}} = \mathbf{I}_{3} - \mathbf{P}_{\color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)}} $$
Using the SVD, the least squares solution set is given by $$ \boxed{ x_{LS} = \color{blue}{x_{p}} + \color{red}{x_{h}} = %% \mathbf{A}^{\dagger}b + \left( \mathbf{I}_{n} - \mathbf{A}^{\dagger} \mathbf{A}\right) y = \frac{1}{6} \color{blue}{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right]} + \frac{1}{6} \left[ \begin{array}{rcr} 5 & 1 & -2 \\ 1 & 5 & 2\\ -2 & 2 & 2 \end{array} \right]y , \qquad y\in\mathbb{R}^{n}} $$
