Finding $\frac {d(\tan \theta)}{d\theta}$

Question

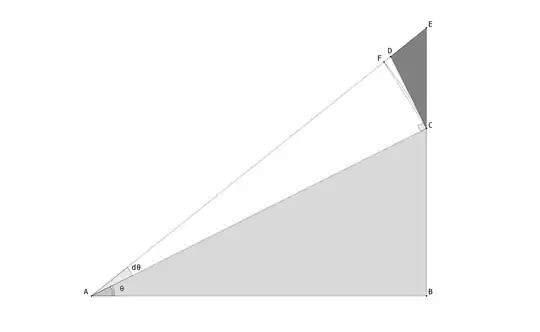
I was reading Needham's Visual Complex Analysis, and could not figure out how we get length $Ld\theta$ here:

Answer 1

It is just an approximation of the arc length of that sector with radius $L$ and angle $dθ$. Note that such a method as presented in that text is totally not rigorous, and will not help you learn to rigorously prove anything in complex analysis!

Answer 2

By "ultimately similar" Needham means the following (see pages 20–21):

We stress here the words "ultimately equal" and "infinitesimal" are being used in delicate, technical senses; in particular, "infinitesimal" does not refer to some mystical, infinitely small quantity⁷. More precisely, if two quantities $X$ and $Y$ depend on a third quantity $\delta$, then \begin{align*} \lim_{\delta \to 0} \frac{X}{Y}\quad & \iff \quad \text{"$X = Y$ for infinitesimal $\delta$".}\\ &\iff \quad \text{"$X$ and $Y$ are ultimately equal as $\delta$ tends to zero".} \end{align*} It follows from the basic theorems on limits that "ultimate equality" inherits many of the properties of ordinary equality.

^{7For more on this distinction, see the discussion in Chandrasekhar [1995].}

Since two triangles are similar if and only if they have the same set of (internal) angles when Needham says that "the black triangle is ultimately similar [exercise] to the shaded triangle" he probably means that the ratio of any angle of the black triangle with the corresponding angle of the shaded triangle tends to $1$ as $d\theta$ tends to zero.

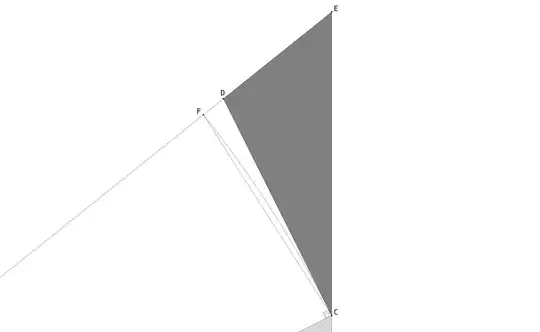
Let the shaded triangle be labelled $\triangle \mathit{ABC}$, where $\angle A = \theta$ and $\angle B = \pi/2$. The black triangle $\triangle\mathit{CDE}$ is obtained by constructing the perpendicular to the line segment $\mathit{AC}$ at $C$ and taking the point $D$ to be where it meets the straight line that is at an angle of $\theta + d\theta$ to the base $\mathit{AB}$, and by extending the segment $\mathit{BC}$ until it meets the same line at the point $E$.

Let us compute the angles of $\triangle \mathit{CDE}$. Examining $\triangle \mathit{ABE}$, we have $\angle E = \pi/2 - \theta - d\theta$ in $\triangle \mathit{CDE}$. Examining $\triangle \mathit{ACD}$, we have $\angle D$ in this triangle to be $\pi/2 - d\theta$. Hence, $\angle D$ in $\triangle \mathit{CDE}$ equals $\pi/2 + d\theta$. Thus, we must have $\angle C$ in $\triangle \mathit{CDE}$ to be equal to $\theta$ (this could also have been seen directly from our construction of $\triangle \mathit{CDE}$).

So, what do the ratios of corresponding angles between $\triangle \mathit{ABC}$ and $\triangle{\mathit{CDE}}$ look like in the limit as $d\theta \to 0$? \begin{align*} &\lim_{d\theta \to 0} \frac{\angle \mathit{CAB}}{\angle \mathit{DCE}} = \lim_{d\theta \to 0} \frac{\theta}{\theta} = 1.\\ &\lim_{d\theta \to 0} \frac{\angle \mathit{BCA}}{\angle \mathit{CED}} = \lim_{d\theta \to 0} \frac{\pi/2 - \theta}{\pi/2 - \theta - d\theta} = 1.\\ &\lim_{d\theta \to 0} \frac{\angle \mathit{ABC}}{\angle \mathit{EDC}} = \lim_{d\theta \to 0} \frac{\pi/2}{\pi/2 + d\theta} = 1.\\ \end{align*}

This proves that the black triangle and shaded triangle in Needham's diagram are ultimately similar. (Of course, we could have just done this for any two angles, since the third angle of a triangle is uniquely determined once the other two are specified.)

---

Now, call $\lvert \mathit{CE} \rvert$ to be $dT$. What can we say about $\lvert \mathit{CD} \rvert$? Let $F$ be the point on the segment $\mathit{AD}$ such that $\lvert \mathit{AF} \rvert = \lvert \mathit{AC} \rvert = L$. Then, certainly $\lvert \mathit{CF} \rvert < L\, d\theta < \lvert \mathit{CD} \rvert$. So, to show that $L\, d\theta$ and $\lvert \mathit{CD} \rvert$ are ultimately equal, it suffices to show that $\lvert \mathit{CF} \rvert$ and $\lvert \mathit{CD} \rvert$ are ultimately equal.

Applying the cosine law on $\triangle \mathit{ACF}$, we get $$ \cos(d\theta) = \frac{L^2 + L^2 - \lvert \mathit{CF} \rvert^2}{2^{\vphantom{2}}\!\;\! L^2} \implies \lvert \mathit{CF} \rvert = 2L\sin\left(\frac{d\theta}{2}\right). $$ Examining $\triangle \mathit{ACD}$, we have $$\tan(d\theta) = \frac{\lvert \mathit{CD} \rvert }{ L } \implies \lvert \mathit{CD} \rvert = \frac{2L\tan \left(\frac{d\theta}{2}\right)}{1^\vphantom{2}\! - \tan^2 \left(\frac{d\theta}{2}\right)}. $$ Thus, $$ \frac{\lvert \mathit{CF} \rvert}{\lvert \mathit{CD} \rvert} = \cos\left(\frac{d\theta}{2}\right) \cdot \left(1 - \tan^2\left(\frac{d\theta}{2}\right)\right). $$ As $d\theta$ tends to $0$ the RHS tends to $1$, so $\lvert \mathit{CF} \rvert$ and $\lvert \mathit{CD} \rvert$ are ultimately equal.

To summarise, the ratio $\dfrac{\lvert \mathit{CE} \rvert}{\lvert \mathit{CD} \rvert}$ is ultimately equal to $\dfrac{\lvert \mathit{AC} \rvert}{\lvert \mathit{AB} \rvert}$ because $\triangle \mathit{CDE}$ is ultimately similar to $\triangle \mathit{ABC}$, and $\lvert \mathit{CD} \rvert$ is ultimately equal to $L\, d\theta$. Thus, $\dfrac{dT}{L\, d\theta}$ is ultimately equal to $\dfrac{L}{1}$, so we get $$ \frac{dT}{d\theta} = L^2 = 1 + T^2 $$ in the limit as $d\theta \to 0$.

---

^{The reference to Chandrasekhar [1995] mentioned in footnote 7 in the quote at the beginning is listed on page 574 as follows: S. Chandrasekhar (1995), Newton's Principia for the Common Reader. Clarendon Press, Oxford.}