1

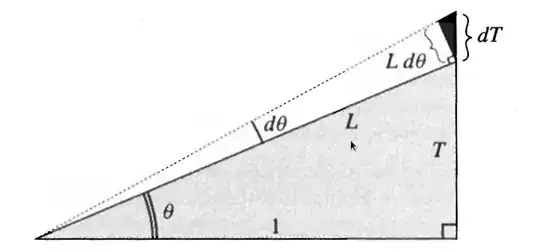
The following picture is taken from the book Visual Complex Analysis by Needham:

enter image description here

The author says that in the limit as $d\theta$ tends to zero, the black triangle is similar to the shaded triangle. I'm not sure what he means by black triangle and shaded triangle but I'm assuming the black triangle is the one with sides $dT$ and $Ld\theta$ and the shaded triangle is the the one with sides $L$ and $T$ and another side with length 1.

If so, why are they similar "in the limit"? How can we know that the dark black area tends to $0$ fast enough comparatively to the light black area?

Also, assuming they are indeed similar, then the angle between $L$ and $T$ is $90º-\theta$ so the angle between $Ld\theta$ and $dT$ should be $\theta$, right? Then shouldn't $\frac{dT}{Ld\theta} = \frac{1}{L}$? But in the book it says $\frac{dT}{Ld\theta} = \frac{L}{1}$...

CcVHKakalLLOOPPOkKkkKk
  • 796

1 Answers1

1

Two triangles are similar if they have the same angles. If $d\theta$ is very small, then the black traingle is almost a right triangle, because the dotted line is almost parallel to line $L$. As you have noticed, the angle between $Ld\theta$ and $dT$ is exactly $\theta$ (even without taking the limit), so that's a second matching angle. Then the third must also match. Strictly speaking, the angles of the black triangle are $\theta$, $\frac{\pi}{2}-\theta-d\theta$ and $\frac{\pi}{2} + d\theta$, and in the limit they tend to the angles of the gray triangle; thus similarity in the limit.

$dT$ is the hypotenuse of black triangle, and $L d\theta$ is the leg adjacent to angle $\theta$; you compare them to the corresponding sides of the big triangle, obtaining $$ \frac{dT}{L d\theta} = \frac{\text{the hypontenuse}}{\text{the leg}} = \frac{L}{1}$$

Adam Latosiński
  • 10,558