2

I started to flick through Needham's Visual Complex Analysis and pretty much fell on my face in the first exercise.

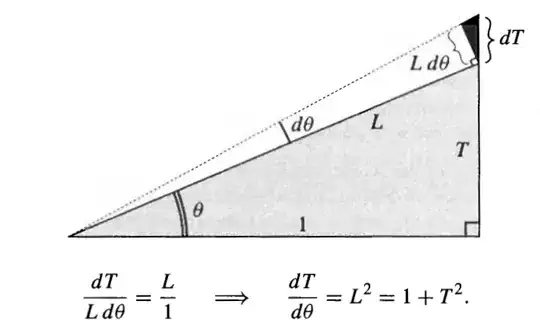
On page ix, he shows a proof that $dT/d\Theta = 1 + T^2$ if $T = tan(\Theta)$.

He does so by comparing the black triangle with the initial triangle (grey). What I don't understand is why the length of the one segment is $L*d\Theta$. I'm sure I'm lacking some basic math here.....

Shouldn't the length be $L*tan(d\Theta)$ (which obviously would be less helpful)?

Needham - Visual Complex Analysis; triangle to proof the above formula

pandita
  • 121

2 Answers2

2

Since $d\theta $ is small, he is approximating the side of the triangle with the length of the curve which is $L d\theta$ when $\theta$ is in radians.

RSS
  • 405
  • What curve?${}{}{}{}{}$ – DonAntonio Dec 17 '16 at 20:54
  • @DonAntonio that which is of length $L d\theta $ i.e. a circular arc? – RSS Dec 17 '16 at 21:08
  • Thanks. Perhaps that it so. I can't though see why would they (or Newton) do such an assumption without explaining it... – DonAntonio Dec 17 '16 at 21:21
  • How big is the error when comparing the arc to the segment? As an engineer I'm fine with this as an estimate, just curious if this is an exact assumption and if not if the reasoning for it is going beyond "good enough" (not that there is anything wrong with that....) – pandita Dec 17 '16 at 23:43
  • @pandita the error is exactly as big as the residual terms in the Taylor series expansion. This is just the geometric version of that argument. You can calculate the error to arbitrary precision. – RSS Dec 18 '16 at 00:40
1

Remember the Taylor Series for $\tan(x)$ about $0$! You find that $\tan x \sim x$ cutting off the series to the most significant term. Otherwise, you are completely right that it should be $L \tan(d\Theta) $ by basic trigonometry... Now apply the Taylor Series.

Note from Comments:
In the event you want to prove the first term of the Taylor Expansion geometrically, use the well known, geometric proofs of $\sin x \sim x$ and $1-\cos x \sim 0 \implies \cos x \sim 1$ by drawing triangles and comparing chord and arc lengths, noting that $\tan x = \frac{\sin x}{\cos x} $

Brevan Ellefsen
  • 14,793
  • I don't think this works at all: if you're trying to deduce the derivative of $;\tan x;$ , and even withut analysis but only elementary trigonometry, using Taylor series seems to be a huge anachrnism here, not even an overkill... – DonAntonio Dec 17 '16 at 21:23
  • @DonAntonio it's a complex analysis textbook, which takes place after a basic real analysis course. Taylor Series are a basic Calculus topic, which is part of real analysis course. You can prove the Taylor Expansion for tangent using the well known, geometric proofs of $\sin x \sim x$ and $1-\cos x \sim x$, noting that $\tan x = \frac{\sin x}{\cos x} $ – Brevan Ellefsen Dec 17 '16 at 21:41
  • So I would say $\tan x = (1-x)^{-1}$ and build the Taylor series around that, right? Sorry last I properly used these things was a rather long time ago at uni. With these approximations in general, would it be required to show that the errors either cancel each other out or approach 0? – pandita Dec 17 '16 at 23:37
  • @pandita not quite sure I understand what you're saying. Constructing the Taylor Series directly could be viewed as a circular argument, because that's what you desire to prove here (it requires the derivative of $\tan x$) That's why I recommend you only get a first-order approximation, which only requires a geometric argument that can be found many places. I outline what you need to prove it in my "Note from Comments"... For proofs of the claims in that part of my post, look for the common, geometric proof that $\lim_{x \to 0} \frac{\sin x}{x} = 1$. (this is equivalent to $\sin x \sim x$) – Brevan Ellefsen Dec 17 '16 at 23:49
  • @pandita you will also have to use $\lim_{x \to 0} \frac{1-\cos x}{x} =0$, which will be found in the proof of the (sin x)/x limit. This is basically saying that $\cos(x) $ approaches $1$ smoothly as $x$ approaches $0$. A continuity argument might also suffice and be a bit more geometric and visual in nature – Brevan Ellefsen Dec 17 '16 at 23:50
  • Thanks Brevan, I looked at your comment in response to DonAntonio, which I believe had a typo (?), where it says $1-\cos x \sim x$. It makes sense in the edit in your answer. Thanks for helping with this. – pandita Dec 18 '16 at 00:04
  • @BrevanEllefsen I think it doesn't matter the book is on complex analysis: they're giving just an example in the preface of a geometric approach of a rather simple fact. Using stuff of advanced analytical nature is, imo, incongruent in the example, thogh I guess anyone of us could use that to support the result – DonAntonio Dec 18 '16 at 07:21
  • @DonAntonio Fair enough. I mean, the informal way to solve this problem is to use the method in the answers by @foofaafuu; I haven't ever been pleased with such an answer though, because it assumes that an infinitesimal segment of a circle can be treated as an infinitesimal line segment. This does work here (keyword: derivative) but doesn't work in general... Take a visual fractal for example, like the Koch Snowflake. In my mind, I need at least enough rigour to show that we can stretch out an infinitely small piece of a smooth curve to get an infinitesimal line segment. – Brevan Ellefsen Dec 18 '16 at 14:52
  • @DonAntonio using the geometrical proof is enough for me though. It's a bit of a heavy hitter with some of the tedium in the proof, but it's more consistent in my mind and easier to justify $\sin \theta \approx \theta$ for small $\theta$ – Brevan Ellefsen Dec 18 '16 at 14:55