34

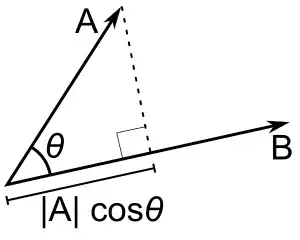
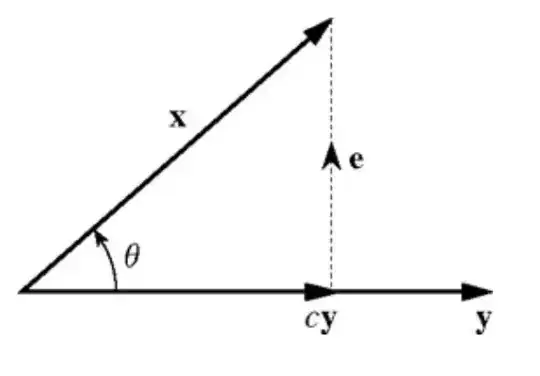
I'm not looking for a mathematical proof; I'm looking for a visual one. I'm having trouble understanding (in my mind's eye) why the dot product of two vectors V and W produces a scalar that is less than the length of V multiplied by the length of W.

In using the dot product, we are producing a parallel vector, correct? Could we not further say that we are simply applying vector W to vector V in order to produce a vector that is the original length of V multiplied by the length of W -- thus a vector parallel to V? For example, if we let vector W be a unit vector (with length of one), then the dot product of V and W would give us a scalar that, when applied to V, produces V again. Would this not be the same as the length of V multiplied by the length of W (given that the length of W is equal to one)?

For that reason, why wouldn't the dot product of V and W always be equal to the length of V multiplied by the length of W? Why would it be less (unless V = cW for any scalar c?)

Martin Sleziak
  • 53,687
Sydney Maples
  • 465
  • 9
    "In using the dot product, we are producing a parallel vector, correct?" The dot product is a scalar quantity, not a vector. – Rammus Jul 26 '15 at 01:56
  • 1
    Consider two vectors A and B, we can contrive to have the magnitudes of A and B be unity for this visualization. A.B represents the 'projection' of A onto B, that is the component of A which is in the same direction as B. Unless A and B are parallel, the projection of A onto B would always be less in size than A. If you diagram this out, you'll see that A.B is |A||B|cos(theta), or just cos(theta) where theta is the angle between A and B ( and |A|=|B|=1). This is in fact a very powerful concept in vector analysis and is used widely in applications. – user247608 Jul 26 '15 at 01:58
  • For those who don't know http://www.maths.kisogo.com/index.php?title=Cauchy-Schwarz_inequality (both definitions) – Alec Teal Jul 26 '15 at 02:01
  • I was under the impression that the scalar quantity applied to a vector V produced a parallel vector. Apologies for the terrible wording. – Sydney Maples Jul 26 '15 at 02:23
  • I don't think there is any visual proof. The numerous answers below, for instances, are somewhat cyclic -- they just build the inequality into the definition of dot product ($\langle u,v\rangle :=|u||v|\cos\theta$). In contrast, the usual and widely accepted proof, that also generalises to general inner products, only relies on the non-negativity of $f(t)=\langle u-tv,u-tv\rangle$. Cauchy-Schwarz inequality in this case is just a simple consequence of solving the least square problem $\min_{t\in\mathbb R}f(t)$. This is not "visual", but arguably very intuitive and elegant. – user1551 Aug 17 '17 at 13:20
  • The C-S Inequality for sums/integrals can be quickly deduced from the trivial and intuitive inequality $(x-y)^2 \geq 0$. – JavaMan Mar 06 '19 at 22:23

6 Answers6

45

In the Cauchy–Schwarz (CS) inequality $|u\cdot v|\le \|u\|\|v\|$, let's assume $v$ is a normalised vector, i.e., $\|v\|=1$. Then the CS inequality becomes $|u\cdot v|\le \|u\|$. Now, it's a trivial matter to show that these two forms of the CS inequality are in fact equivalent, in the sense that if $|u\cdot v|\le \|u\|$ for all normalised vectors $v$, then the usual CS inequality holds for all vectors. So, let us restate the CS inequality as stating that $|u\cdot v|\le \|u\|$ for all normalised vectors $v$. Now, the physical/geometric interpretation of $u\cdot v$ in this case is that it is the component of the vector $u$ in the direction $v$ (since $v$ is assumed normalised, that's all it is, a direction), while $\|u\|$ is the magnitude of $u$. So the CS inequality is merely stating the intuitively obvious fact that the component of a vector $u$ in a single direction is bounded by the magnitude of $u$.

Incidentally, this line of thought carries on to produce a very short and elegant proof of the full CS inequality. But, as you are not looking for a proof, I'll leave that out as an exercise.

Ittay Weiss
  • 79,840
  • 7
  • 141
  • 236
  • 8
    I feel like the hard part is understanding why dot product has anything to do with projection in the first place. Why does the sum of a componentwise product tell you something about the vectors' projection? Is it just me, or is this a completely non-obvious fact that everyone takes for granted? – user541686 Jul 26 '15 at 09:03
  • 1
    @Mehrdad it's often useful to take the dot product to be defined by the requirement that it gives something related to the length of a projection. But in that case, you're right: the fact that one can use $\sum_i a_i b_i$ to calculate the dot product is not obvious. – David Z Jul 26 '15 at 09:45
  • @DavidZ: That's not quite what I meant. I meant that (geometrically and intuitively) projection has to do with the (cosine of) the angle between the vectors. Why should the (cosine of) the angle have anything whatsoever to do with the dot product of the two vectors? It's not at all obvious to me that the two might have any significant relationship, yet they do. – user541686 Jul 26 '15 at 09:48
  • @Mehrdad but you just said you accept that projection has to do with the cosine of the angle. And you know projection is related to the dot product. I don't see where the confusion comes up. (Maybe we should discuss in chat?) – David Z Jul 26 '15 at 09:51
  • @DavidZ: Nope, read my previous comments again. I literally said "the hard part is understanding why dot product has anything to do with projection in the first place". i.e., no, I don't already "know" that the dot product has to do anything whatsoever with the projection or with the angle. That fact is precisely what I'm calling out as non-obvious here. – user541686 Jul 26 '15 at 09:53
  • 2
    @Mehrdad the relation to the cosine (law) may be not the best way to see that. I like to think of it in terms of orthonormal basis. Given an orthonormal basis, any vector $u$ is simply $\sum_i (u\cdot v_i) \cdot v_i$ by a trivial computation which has nothing to do with CW or the law of cosines. This trivially shows that the dot product gives the components of a vector. When teaching these things I like to use the law of cosines to motivate the definition of the standard inner product. Then CS is shown to relate to a law of cosines (kind of) for any inner product. – Ittay Weiss Jul 26 '15 at 09:59
  • @Mehrdad well that's what I said a few comments back: the dot product is (for our purposes) defined by the projection. To be precise: given $\vec{A}$ and $\vec{B}$, and letting $A_B$ denote the projection of $\vec{A}$ on to $\vec{B}$, the dot product is (again, for our purposes) defined as the scalar value $A_B\lVert\vec{B}\rVert$. I think that makes it quite clear what the dot product has to do with projection. If you still don't think so, perhaps you can explain? – David Z Jul 26 '15 at 10:00
  • @DavidZ: Well if you define dot product that way then I guess my problem is that it's not obvious to me why the dot product is the sum of the componentwise products. – user541686 Jul 26 '15 at 10:03
  • @Mehrdad OK I think we understand each other. And in that case Ittay's comment provides the connection I think you're looking for. – David Z Jul 26 '15 at 10:06
  • @IttayWeiss: OK, I see what you're saying, but while the proof you mentioned is trivial to justify, I think it's not at all trivial to to derive in the first place. How is a student supposed to know that he should go through the extra step of decomposing the vector with respect to an entire orthonormal basis merely to show that the weight of one vector in that orthonormal basis is the desired dot product? – user541686 Jul 26 '15 at 10:31
  • @Mehrdad that student can be shown this fact, or requested to clarify the intuition in an exercise. – Ittay Weiss Jul 26 '15 at 10:37
  • 1
    @Mehrdad...Grant sanderson has beautifully explained the connection of dot product with projection in one of his video...I will add link – ogirkar Oct 07 '19 at 02:43
  • 1
    https://youtu.be/LyGKycYT2v0 – ogirkar Oct 07 '19 at 02:45
6

By definition, the "dot" product of two vectors, say $\vec A$ and $\vec B$ is

$$\vec A\cdot \vec B=|\vec A||\vec B|\cos \theta$$

where $\theta$ is the angle between $\vec A$ and $\vec B$. That is to say, that the inner product is the projection of one vector onto the other. Visually, the projection is like a "shadow" that one vector casts along the direction of the other.

Mark Viola
  • 179,405
4

One can show that in Euclidean space, the angle $\theta$ between two vectors $v,w$ (in the sense of Euclidean geometry) satisfies

$$\cos(\theta)=\frac{v \cdot w}{\| v \| \| w \|}.$$

This is basically the law of cosines applied to an appropriate triangle. This equation only makes sense for every $v,w$ if the Cauchy-Schwarz inequality holds.

Ian
  • 101,645
3

Recall that $$a\cdot b=|a||b|\cos\theta$$ where $\theta$ is the angle between $a$ and $b$.

Using this fact it is easy to check that $\dfrac{a\cdot b}{|b|}$ is the component of $a$ in the direction of $b$. Of course the component of $a$ in the direction of $b$ must have absolute value less than or equal to the magnitude of $a$. This gives $\dfrac{|a\cdot b|}{|b|}\leq|a|$ and hence $|a\cdot b|\leq |a||b|$.

So really $a\cdot b=|a||b|\cos\theta$ gives not only a formal proof of the Cauchy-Schwarz inequality, but also a geometric way of thinking of the dot product that makes the Cauchy-Schwarz inequality clear.

Seth
  • 9,393
  • 1
  • 27
  • 64
  • beware a circular argument: it is the CS inequality that allows one to define $\theta$ in the first place. – Ittay Weiss Jul 26 '15 at 10:01
  • 2
    @IttayWeiss I'm really thinking about vectors in $\mathbb{R}^n$ here. In this case $\theta$ has a clear meaning without CS and one can prove the above formula using the law of cosine's (as I'm sure you know). I just finished teaching calc 3 so I got into the habbit of thinking concretely about some of these things. – Seth Jul 26 '15 at 12:34
1

Dot product as projection

(Adapted from wikimedia commons: File:Dot Product.svg using Inkscape 0.91 to convert to PNG.)

The image illustrates the scalar projection of $\mathbf{A}$ onto $\mathbf{B}$, sometimes denoted $A_B$. You already know that, if $||\mathbf{B}||=1$, $\mathbf{A} \cdot \mathbf{B} = A_B$, and so for nonspecial $\mathbf{B}$, $$ \mathbf{A} \cdot \mathbf{B} = \mathbf{A} \cdot \hat{\mathbf{B}}||\mathbf{B}|| = A_B ||\mathbf{B}|| = ||\mathbf{A}|| \, ||\mathbf{B}|| \cos \theta$$ where $\hat{\mathbf{B}}$ denotes the unit vector along $\mathbf{B}$.

But what does this tell us? That $\mathbf{A} \cdot \mathbf{B}$ is maximized when $\theta$ is 90 degrees. In that case, the parallelogram $\mathbf{0}, \mathbf{A} , \mathbf{A} + \mathbf{B}, \mathbf{A} + \mathbf{B} - \mathbf{A} ({}=\mathbf{B})$ is a rectangle. Using the area formula for parallelograms (base times height), the area is maximized when $\mathbf{A}$ is all height. When $\theta$ is not a right angle, the area is less, decreasing to zero as $\mathbf{A}$ and $\mathbf{B}$ become (anti-)parallel.

Community
  • 1
Eric Towers
  • 67,037
1

@Mehrdad

I had the same question as you have expressed:

I feel like the hard part is understanding why dot product has anything to do with projection in the first place. Why does the sum of a componentwise product tell you something about the vectors' projection?

After some thinking, I come up with the following reasoning, not sure if it make sense to you.

enter image description here

  1. In Section 6.5-1 of Lathi’s Linear Systems and Signals, 2nd, projection of $\mathbf{x}$ along $\mathbf{y}$ can be interpreted as a way to minimize the "error" $\mathbf{e}$, when $\mathbf{x}$ is expressed as $\mathbf{x}=c\mathbf{y}+\mathbf{e}$, where $c\mathbf{y}$ is the component of $\mathbf{a}$ in the direction of $\mathbf{b}$, and $\mathbf{e}$ is the "error" vector, which has the minimum length when it's perpendicular to $\mathbf{b}$.

  2. Btw: the "error" vector gives hints on how much $\mathbf{x}$ is differ from $c\mathbf{y}$. In this sense, projection is a way to find similarities of two vectors, and this may explain why correlation is calculated exactly in the same way as dot product.

  3. Now the question can be rephrased as: why product has anything to do with correlation/similarity? Let's take plain numbers (not vectors) for now. To find difference between two numbers $a$ and $b$, we do subtraction $a-b$, which can be either positive or negative. Most of the time people only cares about the absolute value of the difference $|a-b|$, but $|a-b|$ is not convenient in mathematical manipulation. So people square the difference, $(a-b)^2$...this is where the product comes in. The formula $(a-b)^2=a^2+b^2-2ab$ suggests that the product $ab$ has its place as a measure of the difference or similarity between $a$ and $b$.

bruin
  • 257
  • Inner product has to do with projection because with $x = ay+z$, $a = \frac{\langle x,y \rangle}{\langle y,y \rangle}$, $z = x-ay$ then $\langle z,y\rangle = 0$. Why is it useful ? Because $|u+v|^2 = |u|^2+|v|^2-2 \langle u,v \rangle$, the norm being assumed to be useful – reuns Aug 17 '17 at 07:32