New Idea to prove $1+2x+3x^2+\cdots=(1-x)^{-2}$

Question

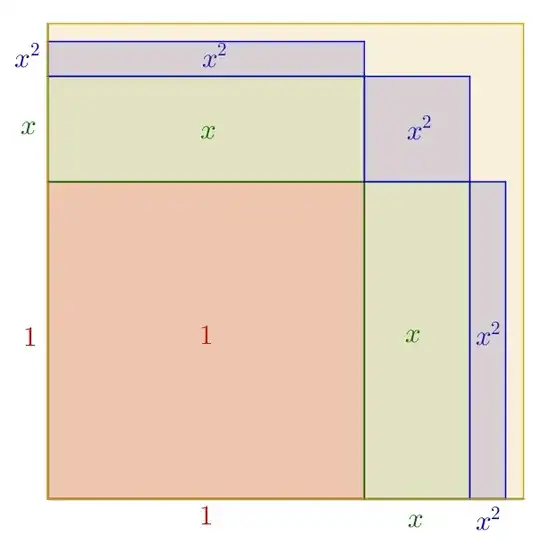
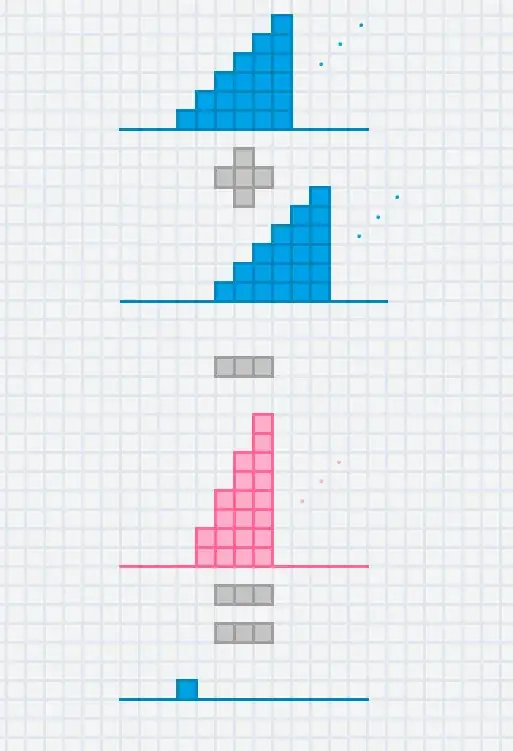
Given $|x|<1 $ prove that $\\1+2x+3x^2+4x^3+5x^4+...=\frac{1}{(1-x)^2}$.

1st Proof: Let $s$ be defined as $$ s=1+2x+3x^2+4x^3+5x^4+\cdots $$

Then we have

$$ \begin{align} xs&=x+2x^2+3x^3+4x^4+5x^5+\cdots\\ s-xs&=1+(2x-x)+(3x^2-2x^2)+\cdots\\ s-xs&=1+x+x^2+x^3+\cdots\\ s-xs&=\frac{1}{1-x}\\ s(1-x)&=\frac{1}{1-x}\\ s&= \frac{1}{(1-x)^2} \end{align} $$

2nd proof:

$$ \begin{align} s&=1+2x+3x^2+4x^3+5x^4+\cdots\\ &=\left(1+x+x^2+x^3+\cdots\right)'\\ &=\left(\frac{1}{1-x}\right)'\\ &=\frac{0-(-1)}{(1-x)^2}\\ &=\frac{1}{(1-x)^2} \end{align} $$

3rd Proof:

$$ \begin{align} s=&1+2x+3x^2+4x^3+5x^4+\cdots\\ =&1+x+x^2+x^3+x^4+x^5+\cdots\\ &+0+x+x^2+x^3+x^4+x^5+\cdots\\ &+0+0+x^2+x^3+x^4+x^5+\cdots\\ &+0+0+0+x^3+x^4+x^5+\cdots\\ &+\cdots \end{align} $$ $$ \begin{align} s&=\frac{1}{1-x}+\frac{x}{1-x}+\frac{x^2}{1-x}+\frac{x^3}{1-x}+\cdots\\ &=\frac{1+x+x^2+x^3+x^4+x^5+...}{1-x}\\ &=\frac{\frac{1}{1-x}}{1-x}\\ &=\frac{1}{(1-x)^2} \end{align} $$

These are my three proofs to date. I'm looking for more ways to prove the statement.

Answer 1

$${1\over(1-x)^2}={1\over 1-x}\cdot{1\over 1-x}=\sum_{j\geq0} x^j\cdot\sum_{k\geq0}x^k =\sum_{r\geq0} x^r\left(\sum_{j+k=r}1\right)=\sum_{r\geq0}(r+1)x^r\ .$$

Answer 2

For the special case $x=\dfrac12$:

If you accept that $1+x+x^2+\dotsb=\dfrac1{1-x}$, the same picture works — just move the horizontal and vertical lines. Instead of them being at $1,1\frac12,1\frac34,\dotsb,2$, you should put them at $1,1+x,1+x+x^2,\dotsb,\dfrac1{1-x}$. The area of the square is then $\left(\dfrac1{1-x}\right){}^2$.

Answer 3

Not a visual proof, but by the Binomial Theorem, $$(1-x)^{-2}=\sum_0^{\infty}{-2\choose n}(-1)^nx^n$$ Now $${-2\choose n}={-2\cdot-3\cdots(-1-n)\over n!}=(-1)^n(n+1)$$ so $(1-x)^{-2}=\sum_0^{\infty}(n+1)x^n$, as desired.

Answer 4

Let $S=1+2x+3x^2+4x^3+\dotsb$. \begin{align} \phantom{-x^2}S&=1+2x+3x^2+4x^3+\dotsb\\ \phantom{^2}-xS&=\phantom1-\phantom2x-2x^2-3x^3-\dotsb\\ \phantom{^2}-xS&=\phantom1-\phantom2x-2x^2-3x^3-\dotsb\\ \phantom{-}x^2S&=\phantom{1+2x+2}x^2+2x^3+\dotsb \end{align} Adding them together: \begin{align} (1-2x&+x^2)S\\ &=1+0x+0x^2+0x^3+\dotsb\\ &=1\\ S&=\frac1{1-2x+x^2} \end{align}

Answer 5

The effect of multiplication by $1/(1-x)$ to the sequence of coefficients is to calculate partial sums: if the original sequence is $c_0,c_1,\ldots$ then the new one is $$ d_i = c_0 + \cdots + c_i. $$ The starting point is the sequence $1,0,0,\ldots$. Applying this operator twice, we get $$ 1,0,0,0,0,\ldots \\ 1,1,1,1,1,\ldots \\ 1,2,3,4,5,\ldots $$ In this matrix, the first row is given, the first column is constant, and otherwise the value of a cell is the sum of the cell above it and the cell to its left.

I'll let you figure out the connection to Pascal's triangle on your own.

Answer 6

Problem: For a given integer $N$, how many integers $n_1$ and $n_2$ larger than or equal to zero are there that satisfy the equation:

$$n_1 + n_2 = N$$

We note that it is the coefficient of $x^N$ in the expansion of

$$\left(\sum_{k=0}^{\infty}x^k\right)^2 = \frac{1}{(1-x)^2}$$

We can also solve the problem by noting that it is the number of ways you can color N objects with 2 colors. The count the number of solutions, we note that there is aone to one correspondence between colorings and a string consisting of N 0's and one 1. The 0's to the left of the 1 represent to objects with color 1 the 0's to the right represent the objects with color 2. The total number of such strings is equal to $\binom{N+1}{1} = N+1$. This means that the coefficient of $x^N$ in $\frac{1}{(1-x)^2}$ is equal to $N+1$.

Answer 7

Let $X \sim G(1-x)$, a geometric random variable with success probability $1-x$. We have $$ \mathbb{E}[X] = \sum_{n=1}^\infty nx^{n-1}(1-x). $$ On the other hand, we know that $\mathbb{E}[X] = 1/(1-x)$, and we deduce the formula.

We can argue that $\mathbb{E}[X] = 1/(1-x)$ in many ways. One way is to consider $N$ different trials with success probability $1-x$. The number of successful trials is roughly $(1-x)N$, and so the average distance between successful ones (which is distributed according to $X$) is roughly $N/((1-x)N) = 1/(1-x)$. (This argument can be formalized.)

Answer 8

As I'd suggested like Calculating $1+\frac13+\frac{1\cdot3}{3\cdot6}+\frac{1\cdot3\cdot5}{3\cdot6\cdot9}+\frac{1\cdot3\cdot5\cdot7}{3\cdot6\cdot9\cdot12}+\dots? $,

Using Generalized Binomial Expansion, $$(1+y)^n=1+ny+\frac{n(n-1)}{2!}y^2+\frac{n(n-1)(n-2)}{3!}y^3+\cdots$$ given the converge holds

Comparing with given Series

$ny=2x\ \ \ \ (1)$

$\dfrac{n(n-1)}{2!}y^2=3x^2\ \ \ \ (2)$

$(1)\implies y=\dfrac{2x}n$

From $(2),3x^2=\dfrac{n(n-1)}2\left(\dfrac{2x}n\right)^2\iff n=-2$ as $x\ne0$ for non-trivial cases

$(1)\implies y=\dfrac{2x}n=\dfrac{2x}{-2}=-x$

Answer 9

Here is another variation.

Assuming the geometric series $\sum_{n=0}^{\infty}x^n=\frac{1}{1-x}$ is known, we consider functions $f,g:(-1,1) \rightarrow \mathbb{R}$

\begin{align*} f(x)&=\sum_{n=0}^{\infty}(n+1)x^n\qquad\qquad g(x)=\frac{1}{(1-x)^2} \end{align*}

We obtain \begin{align*} \int f(x) dx&=\int\left(\sum_{n=0}^{\infty}(n+1)x^n\right) dx =\sum_{n=0}^{\infty}\int(n+1)x^n dx\\ &=\sum_{n=0}^{\infty}x^{n+1}+C=\sum_{n=1}^\infty x^n+C\\ &=\frac{1}{1-x}-1+C\\ \\ \int g(x) dx&= \int \frac{1}{(1-x)²}dx=\frac{1}{1-x}+D \end{align*}

We observe $f$ and $g$ have the same antiderivative $\frac{1}{1-x}$ differing by a constant only. Since $f(0)=g(0)=1$ they are equal.

Answer 10

ie. $(1 - x)^2(1 + 2x + 3x^2 + ...) = 1$

Answer 11

The following proof is far to complicated, but it is a new one and I think it is somewhat funny too.

For $x\in\left[0;1\right)$ we have: $$ \frac{1}{\left(1-x\right)^2}=\frac{1}{1-\left(2x-x^2\right)}=\sum_{k=0}^{\infty}\left(2x-x^2\right)^k=\sum_{k=0}^{\infty}{\sum_{r=0}^{k}\binom{k}{r}(-1)^r2^{k-r}x^{k+r}}=\sum_{k=0}^{\infty}c_kx^k $$ We have $c_{2n}=\sum_{s=0}^{n}{\binom{n+s}{n-s}(-1)^{n-s}2^{2s}}$ and $c_{2n+1}=\sum_{s=0}^{n}{\binom{n+s+1}{n-s}(-1)^{n-s}2^{2s+1}}$. Applying the identity $\binom{n+1}{k+1}=\binom{n}{k}+\binom{n}{k+1}$ we obtain: $$ c_{2n+2}=\sum_{s=0}^{n+1}{\binom{n+1+s}{n+1-s}(-1)^{n+1-s}2^{2s}}=\sum_{s=0}^{n+1}{\binom{n+s}{n-s}(-1)^{n+1-s}2^{2s}}+\sum_{s=0}^{n+1}{\binom{n+s}{n-s+1}(-1)^{n+1-s}2^{2s}}=-c_{2n}+2c_{2n+1} $$ $$ c_{2n+3}=\sum_{s=0}^{n+1}{\binom{n+s+2}{n-s+1}(-1)^{n+1-s}2^{2s+1}}=\sum_{s=0}^{n+1}{\binom{n+s+1}{n-s}(-1)^{n+1-s}2^{2s+1}}+\sum_{s=0}^{n+1}{\binom{n+s+1}{n-s+1}(-1)^{n+1-s}2^{2s+1}}=-c_{2n+1}+2c_{2n+2}=3c_{2n+1}-2c_{2n} $$ Therefore: $$ c_{2n+3}-c_{2n+2}=3c_{2n+1}-2c_{2n}+c_{2n}-2c_{2n+1}=c_{2n+1}-c_{2n}=…=c_1-c_0=1 $$ Thus: $$ c_{2n+2}=-c_{2n}+2\left(c_{2n}+1\right)=c_{2n}+2 $$ $$ c_{2n+3}=3c_{2n+1}-2\left(c_{2n+1}-1\right)=c_{2n+1}+2 $$ Together with $c_0=1$ and $c_1=2$ we obtain $c_n=n+1$. Thus, for $x\in\left[0;1\right)$: $$ \frac{1}{\left(1-x\right)^2}=\sum_{k=0}^{\infty}(k+1)x^k $$ By observing, that: $$ \sum_{k=0}^{\infty}(k+1)(-x)^k+\sum_{k=0}^{\infty}(k+1)x^k=\sum_{k=0}^{\infty}(4k+2)x^2k=\frac{4}{\left(1-x^2\right)^2}-\frac{2}{1-x^2} $$ We get the analogous result for $x\in\left(-1;0\right]$

Answer 12

Let $$ f(x) = \sum_{n = 1}^{\infty} nx^{n-1}, \quad |x| < 1. $$ Then $$f'(x) = \sum_{n = 2}^{\infty} n(n-1)x^{n-2} = 2 \left( \sum_{n=2}^{\infty} \frac{n(n-1)}2x^{n-2} \right ).$$ Note $\frac{n(n-1)}2 = \dbinom{n}2$ so $$f'(x) = 2 \sum_{n=2}^{\infty} \dbinom{n}2x^{n-2} .$$ Now consider the coefficient of $x^k$ in $\frac{1}{(1-x)^3} = (1+x+x^2+ \cdots )^3$.The coefficient of $x^k$ is the number of ways to solve the equation $a+b+c = k$ where $0 \le a,b,c \le k$. Imagine this as $k$ dots where we need to place $2$ bars.

This gives us $\dbinom{k+2}2$ ways. Thus, we have $$ \sum_{n=2}^{\infty} \dbinom{n}2x^{n-2} = \frac{1}{(1-x)^3} $$ so $$f'(x) = \frac{2}{(1-x)^3}$$ so $$f(x) = \int \frac{2}{(1-x)^3} dx = \frac{1}{(1-x)^2} +C. $$ Letting $x = 0$ gives $C = 0$ as desired.

Answer 13

Use differences of a sum.

$$ \begin{array}{r} S &=& +1 & +2 x & +3 x^2 & +4 x^3 & +5 x^4 & +6 x^5 & +7 x^6 & \cdots\\ -2 x S &=& & -2x & -4 x & -6 x^2 & -8 x^3 & -10 x^4 & -12 x^5 & \cdots\\ x^2 S &=& & & +x^2 & +2 x^2 & +3 x^4 & +4 x^5 & +5 x^6 & \cdots\\ &&&&&&&&&& +\\ \hline\\ \big( 1 - 2 x + x^2 \big) S &=& +1 \end{array} $$

Or

$$ \begin{array}{rclc} S &=& \displaystyle + \sum_{k=1}^\infty k x^{k-1}\\ - 2 x S &=& \displaystyle - \sum_{k=1}^\infty 2 k x^{k}\\ x^2 S &=& \displaystyle + \sum_{k=1}^\infty k x^{k+1}\\ &&&+\\ \hline\\ \big( 1 - 2 x + x^2 \big) S &=& \displaystyle \sum_{k=1}^\infty k x^{k-1} - \sum_{k=1}^\infty 2 k x^{k} + \sum_{k=1}^\infty k x^{k+1}\\ &=& \displaystyle \sum_{k=0}^\infty (k+1) x^k - \sum_{k=1}^\infty 2 k x^{k} + \sum_{k=2}^\infty (k-1) x^k\\ &=& \displaystyle 1 + \big[ 2 - 2 \big] x + \sum_{k=2}^\infty \big[ (k+1) - 2 k + (k-1) \big] x^k\\ &=& 1 \end{array} $$

So

$$ S = \frac{1}{1-2x+x^2} = \frac{1}{(1-x)^2} $$

Answer 14

The sequence $y=(1,2,3,4,\ldots)$ is an output of the linear system $$ y_{k+1}=y_k+u_k,\qquad y_0=1 $$ for the input $u=(1,1,1,1,\ldots)$. Perform the $Z$-transform (multiply by $z^k$ and add up for all $k$) $$ \sum_{k=0}^\infty y_{k+1}z^k=\underbrace{\sum_{k=0}^\infty y_kz^k}_{y(z)}+\underbrace{\sum_{k=0}^\infty u_kz^k}_{u(z)}\quad\Rightarrow\quad \frac{1}{z}(y(z)-y_0)=y(z)+u(z)\quad\Rightarrow $$ $$ \Rightarrow\quad y(z)=\frac{1+z u(z)}{1-z}=\frac{1+z\frac{1}{1-z}}{1-z}=\frac{1}{(1-z)^2}. $$

Answer 15

Consider $$(1+x+x^2+x^3+\cdots)(1+x+^2+x^3+\cdots)$$ Coefficient of $x^k$ in this expansion is just $k+1.$ Because $$1.x^k+x.x^{k-1}+x^2.x^{k-2}+\cdots+x^k.1=(k+1)x^k.$$ Therefore $$(1+x+x^2+x^3+\cdots)^2=1+2x+3x^2+4x^3+\cdots.$$ Now evaluate (you can use the same procedure) $$(1-2x+x^2)(1+2x+3x^2+4x^3+\cdots)=?$$