110

Just curious about why geometric progression is called so. Is it related to geometry?

Martin Sleziak
  • 53,687
dark32
  • 1,401

6 Answers6

111

Here's an extremely nice picture illustrating the geometric series and making it geometrically clear how it converges when $x<1$.

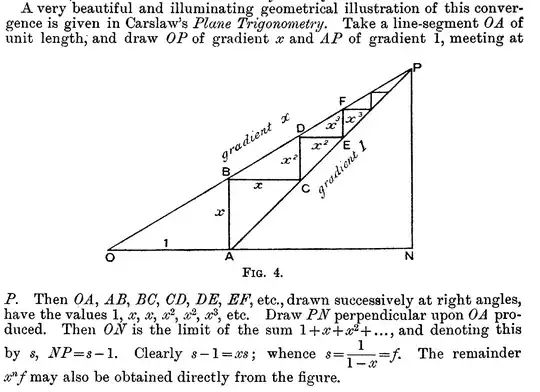
Dobbs 1918

$s-1=xs$ follows from $PN/ON=BA/OA$ which follows from the fact that $\triangle OAB$ is similar to $\triangle ONP$.

em29
  • 95
Gregory Grant
  • 14,874
97

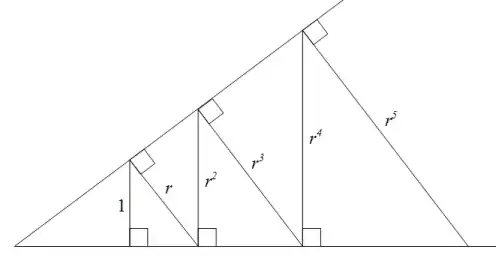
Here is a geometric figure illustrating the geometric progression $1,r,r^2,r^3,r^4,r^5,\ldots$:

enter image description here

David K
  • 98,388
  • 5
    Now that's a good picture! We don't have to worry about whether people were thinking about $8$-dimensional cubes, however long ago the terminology came about. – pjs36 May 14 '15 at 14:26
  • 3
    So I guess we pick $r$ and draw the edge you have labelled as $r$. Then the hypotenuse of the resulting triangle is $r^2$? Can you please post a proof of that? Does this depend on the length of the other two edges of the first right triangle (the leftmost one with one leg labelled $1$). You haven't labelled them and they aren't uniquely determined by one leg being length one. Thank you. – Gregory Grant May 14 '15 at 14:37
  • 6
    @GregoryGrant The triangles are all similar, that uniquely determines everything. The second triangle from the bottom is drawn first and then the first triangle is drawn similar to the second and so on... – Asvin May 14 '15 at 14:47
  • I see it now, thanks – Gregory Grant May 14 '15 at 14:55
  • 1
    @GregoryGrant Its pretty easy to proof, you can prove it using the properties of similar triangles. Just do an internet search and you will definitely find a very neat proof. ;) – dark32 May 14 '15 at 15:24
  • 1
    Yes I proved it, the conceptual leap was to realize the second triangle from the bottom is drawn first. Then it's easy to show that all right triangles in this figure are similar which follows from Euclid's most basic propositions on angles and parallel lines. – Gregory Grant May 14 '15 at 15:46
  • 4
    Is there any useful information that can be read off this figure? What would it look like for the interesting case when $r < 1$? – Rob Arthan May 14 '15 at 19:16
  • 9
    @RobArthan If $r<1$, you draw the figure approaching the vertex rather than going away from it. – Mario Carneiro May 15 '15 at 09:13
  • 1
    Beautiful pictorial illustration of the geometric progression when $r\gt1$. However this is not an answer to the question about the provenance of the term "geometric". – Piquito Jun 30 '15 at 03:26
  • 3
    @Ataulfo I've since become aware of this paragraph from the Oxford English Dictionary: "Arithmetical progression, proportion, ratio, etc. ... relate to differences instead of quotients. The term geometrical points to the fact that problems involving multiplication were originally dealt with by geometry and not by arithmetic." That's the best answer I have for the first part of the question. – David K Jun 30 '15 at 04:46
  • 1
    @David K: That´s right. Looking for information about this question I find that hypergeometric series (the prefix “hyper” is well known) are called so because they generalize the geometric series; Pfaff was the mathematician (teacher and friend of Gauss and later Möbius teacher) who introduced this term. – Piquito Jun 30 '15 at 12:29
16

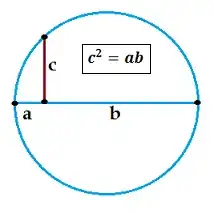
Let $ABC$ is a right triangle with right angle $\angle ABC$, then if we draw the height $BH$, we have $$ |BH|^2=|AH||CH| $$ The geometric mean comes from here...

k1.M
  • 5,428
9

The arithmetic and geometric adjectives come from the Pythagoreans before the Christian Era. Apparently, the expression “geometric progression” comes from the “geometric mean” (Euclidean notion) of segments of length $a$ and $b$: it is the length of the side $c$ of a square whose area is equal to the area of the rectangle of sides $a$ and $b$. The construction of the geometric mean with ruler and compass is well known for high school students; it involves "multiplication" and not "addition".

enter image description here

Piquito
  • 29,594
  • 2
    This picture perfectly explains why the geometric mean is smaller then the arithmetic mean if $a\neq b$. and equal if a=b. Beautiful. By Thales' theorem its the same as the comment of the right triangle – Libertas Aug 08 '20 at 06:53
  • Thank you for your comment, dear friend. – Piquito Aug 09 '20 at 11:08
5

My guess would be that geometric sequences arose as generalization of sequence $a,a^2,a^3,...$. Why is this geometric? Well, $a$ is the length (= 1-dimensional "volume") of line segment (= 1-dimensional hypercube) of "side" length $a$, $a^2$ is the area (= 2-dimensional "volume") of a square (= 2-dimensional hypercube) of side length $a$, $a^3$ is the volume (= 3-dimensional "volume") of a cube (= 3-dimensional hypercube) of side length $a$ and so on.

Wojowu
  • 26,600
2

Because geometric progressions are based on multiplication, and the most important geometric notion, namely, volume, arises from multiplication (length times width times height). The term “multiplicative” is not used because it already has a special meaning in Number Theory.

Mike Jones
  • 4,460