What is the fastest/most efficient algorithm for estimating Euler's Constant $\gamma$?

Question

What is the fastest algorithm for estimating Euler's Constant $\gamma \approx0.57721$?

Using the definition:

$$\lim_{n\to\infty} \sum_{x=1}^{n}\frac{1}{x}-\log n=\gamma$$

I finally get $2$ decimal places of accuracy when $n\geq180$. The third correct decimal place only comes when $n \geq638$. Clearly, this method is not very efficient (it can be expensive to compute $\log$).

What is the best method to use to numerically estimate $\gamma$ efficiently?

Answer 1

The paper "On the computation of the Euler constant $\gamma$" by Ekatharine A. Karatsuba, in Numerical Algorithms 24(2000) 83-97, has a lot to say about this. This link might work for you.

In particular, the author shows that for $k\ge 1$, $$ \gamma= 1-\log k \sum_{r=1}^{12k+1} \frac{ (-1)^{r-1} k^{r+1}}{(r-1)!(r+1)} + \sum_{r=1}^{12k+1} \frac{ (-1)^{r-1} k^{r+1} }{(r-1)! (r+1)^2}+\mbox{O}(2^{-k})$$

and more explicitly $$\begin{align*} -\frac{2}{(12k)!} - 2k^2 e^{-k} \le \gamma -1+&\log k \sum_{r=1}^{12k+1} \frac{ (-1)^{r-1} k^{r+1}}{(r-1)!(r+1)} - \sum_{r=1}^{12k+1} \frac{ (-1)^{r-1} k^{r+1} }{(r-1)! (r+1)^2}\\ &\le \frac{2}{(12k)!} + 2k^2 e^{-k}\end{align*}$$ for $k\ge 1$.

Since the series has fast convergence, you can use these to get good approximations to $\gamma$ fairly quickly.

Answer 2

I like $$ \gamma = \lim_{n \rightarrow \infty} \; \; \left( \; \; 1 + \frac{1}{2} + \cdots + \frac{1}{n} - \frac{1}{n + 1 } - \cdots - \frac{1}{n^2 } - \frac{1}{n^2 + 1 } - \cdots - \frac{1}{n^2 + n} \; \; \right) $$ because it needs no logarithm and the error is comparable to the final term used.

       n                sum                 error                    n^2 * error
       1          0.5                    0.07721566490153287       0.07721566490153287
      10          0.5757019096925315     0.001513755209001322      0.1513755209001322
     100          0.5771991634147917    1.650148674114948e-05      0.1650148674114948
    1000          0.5772154984013406    1.665001923001341e-07      0.1665001923001341
   10000          0.5772156632363485    1.665184323762503e-09      0.1665184323762503

I found this formula on page 82, the January 2012 issue (volume 119, number 1) of the M. A. A. American Mathematical Monthly. It was sent in by someone named Jouzas Juvencijus Macys, possibly for the Problems and Solutions section. He stopped the sum at $-1/n^2.$ I noticed that the error would be minimized by continuing the sum to $-1/(n^2 + n).$ If you want, you can add a single term $1/(6 n^2)$ to get the error down to $n^{-3}.$

$$ \gamma = \lim_{n \rightarrow \infty} \; \; \frac{1}{6n^2} + \left( \; \; 1 + \frac{1}{2} + \cdots + \frac{1}{n} - \frac{1}{n + 1 } - \cdots - \frac{1}{n^2 } - \frac{1}{n^2 + 1 } - \cdots - \frac{1}{n^2 + n} \; \; \right) $$

       n                sum                 error              
       1          0.6666666666666666   -0.08945100176513376
      10          0.5773685763591982   -0.0001529114576653834
     100          0.5772158300814584   -1.651799255153463e-07
    1000          0.5772156650680073   -1.664743898288634e-10
   10000          0.5772156649030152   -1.482369782479509e-12

EDIT, December 2013. I just got a nice note, with English preprint, from Prof. Macys. The original article is in Lithuanian in 2008. A Russian version and matching English translation are both 2013: the Springer website is not quite up to Volume 94, number 5, pages 45-50. The English language journal is called Mathematical Notes. Oh, the title is "On the Euler-Mascheroni constant."

If desired, you can put two correction terms to get the error down to $n^{-4}.$

$$ \gamma = \lim_{n \rightarrow \infty} \; \; \frac{-1}{6n^3} +\frac{1}{6n^2} + \left( \; \; 1 + \frac{1}{2} + \cdots + \frac{1}{n} - \frac{1}{n + 1 } - \cdots - \frac{1}{n^2 } - \cdots - \frac{1}{n^2 + n} \; \; \right) $$

 10  0.5772019096925316  1.375520900126492e-05  
100  0.5772156634147917  1.486741174616668e-09 
600  0.5772156649003506  1.182276498923329e-12  

Answer 3

A good place for fast evaluation of constants is Gourdon and Sebah's 'Numbers, constants and computation'.

They got $108\cdot 10^6$ digits for $\gamma$ in 1999 (see the end of their 2004 article 'The Euler constant') and propose a free program for high precision evaluation of various constants 'PiFast'.

On his page of constants Simon Plouffe has Euler's constants to 10^6 digits (the file looks much smaller sorry...) using Brent's splitting algorithm (see the 1980 paper of Brent 'Some new algorithms for high-precision computation of Euler’s constant' or more recently 3.1 in Haible and Papanikolaou's 'Fast multiprecision evaluation of series of rational numbers').

It seems that the 1999 record was broken in 2009 by A. Yee & R. Chan with 29,844,489,545 digits 'Mathematical Constants - Billions of Digits' (warning: the torrent file proposed there is more than 11Gb large! An earlier 52Mb file of 'only' 116 million digits is available here using the method proposed by Gourdon and Sebah).

Answer 4

(N.B. The previous version of this answer featured both the Brent-McMillan algorithm and the acceleration of Macys's series; I have decided to move the Brent-McMillan material into a new answer in the interest of having only one method per answer.)

---

The convergence properties of Macys's series in Will's answer can be improved a fair bit, if you're willing to devote some amount of computational effort; due to the $n^{-2}$ behavior of the error, one obvious choice for a convergence acceleration method is Richardson extrapolation.

Skipping some hairy details (which I might include later if I find time, but see Marchuk/Shaidurov if you must), the working formula is

$$\gamma=\lim_{n\to\infty} G_n=2\lim_{n\to\infty} \sum_{i=1}^{n+1} \frac{(-1)^{n-i} i^{2n+2}}{(n+i+1)!(n-i+1)!}\left(\sum_{k=i+1}^{i(i+1)} \frac1{k}-\sum_{k=1}^i \frac1{k}\right)$$

Here are some sample results:

$$\begin{array}{ccc}n&G_n&\gamma-G_n\\10&0.577210083083&5.581818\times10^{-6}\\50&0.577215659731&5.170456\times10^{-9}\\100&0.577215664665&2.362333\times10^{-10}\\200&0.577215664891&1.061648\times10^{-11}\\250&0.577215664898&3.902515\times10^{-12}\\300&0.577215664900&1.721878\times10^{-12}\\350&0.577215664901&8.618620\times10^{-13}\end{array}$$

For higher precision, there isn't much of an improvement; I would still recommend Brent-McMillan if one needs many digits of $\gamma$.

Answer 5

Finch's Mathematical Constants mentions these papers:

• D. W. DeTemple, A quicker convergence to Euler's constant, Amer. Math. Monthly (1993) 468-470.
• T. Negoi, A faster convergence to Euler's constant, Math. Gazette 83 (1999) 487-489.

Answer 6

As it turns out, the convergence of the Karatsuba series presented in Matthew's answer can be improved. This time, the geometric behavior of the error (as can be ascertained from the bounds presented) can be exploited through the use of the Shanks transformation. (Richardson can be made to work here as well, but the results are not as spectacular.)

Letting

$$\varepsilon_0^{(k)}=1-\log(k+1) \sum_{r=1}^{12k+13} \frac{ (-k)^{r+1}}{(r-1)!(r+1)} + \sum_{r=1}^{12k+13} \frac{ (-k)^{r+1} }{(r-1)!(r+1)^2}$$

Wynn's version of the Shanks transformation uses the recursion

$$\varepsilon_{k+1}^{(n)}=\varepsilon_{k-1}^{(n+1)}+\frac1{\varepsilon_{k}^{(n+1)}-\varepsilon_k^{(n)}}$$

It would seem that a two-dimensional array would be required for implementation, but one can arrange things such that only a one-dimensional array is required, through clever overwriting. Here is a Mathematica routine to demonstrate:

wynnEpsilon[seq_?VectorQ] := Module[{n = Length[seq], ep, res, v, w},
  res = {};
  Do[
   ep[k] = seq[[k]];
   w = 0;
   Do[
    v = w; w = ep[j];
    ep[j] = 
     v + (If[Abs[ep[j + 1] - w] > 10^-(Precision[w]), ep[j + 1] - w, 
         10^-(Precision[w])])^-1;
    , {j, k - 1, 1, -1}];
   res = {res, ep[If[OddQ[k], 1, 2]]};
   , {k, n}];
  Flatten[res]
  ]

(actually the same as the routine presented in this answer).

Here's a comparison of Karatsuba's series, with and without Shanks transformation:

gamprox = Table[N[1 - Log[k]*Sum[(-k)^(r + 1)/((r + 1)*(r - 1)!),
            {r, 1, 12*k + 1}] + Sum[(-k)^(r + 1)/((r + 1)^2*(r - 1)!),
            {r, 1, 12*k + 1}], 50], {k, 30}];

trans = wynnEpsilon[gamprox];

gamprox[[20]] - EulerGamma // N
1.31827*10^-7

trans[[20]] - EulerGamma // N
6.49869*10^-18

Last[gamprox] - EulerGamma // N
9.96301*10^-12

Last[trans] - EulerGamma // N
2.07059*10^-27

Not too shabby, in my humble opinion...

Answer 7

I quite like the Brent-McMillan algorithm myself (which is based on the relationships between the Euler-Mascheroni constant and modified Bessel functions):

$$\gamma=\lim_{n\to\infty}\mathscr{G}_n=\lim_{n\to\infty}\frac{\sum\limits_{k=0}^\infty \left(\frac{n^k}{k!}\right)^2 (H_k-\log\,n)}{\sum\limits_{k=0}^\infty \left(\frac{n^k}{k!}\right)^2}$$

where $H_k=\sum\limits_{j=1}^k \frac1{j}$ is a harmonic number.

It requires the use of a logarithm, but the algorithm is quite simple and reasonably efficient (in particular, we have the inequality $0 < \mathscr{G}_n-\gamma < \pi\exp(-4n)$).

Here's some Mathematica code for the Brent-McMillan algorithm (which should be easily translatable to your language of choice):

n = 50;
a = u = N[-Log[n], n]; b = v = 1;
i = 1;
While[True,
  k = (n/i)^2;
  a *= k; b *= k;
  a += b/i;
  If[u + a == u || v + b == v, Break[]];
  u += a; v += b;
  i++
  ];
u/v

The integer parameter n controls the accuracy; very roughly, the algorithm will yield n-2 or so correct digits.

The Brent-McMillan paper also presents more elaborate schemes for computing $\gamma$, such as

$$\gamma=\lim_{n\to\infty}\frac{\sum\limits_{k=0}^\infty \left(\frac{n^k}{k!}\right)^2 (H_k-\log\,n)}{\sum\limits_{k=0}^\infty \left(\frac{n^k}{k!}\right)^2}-\frac{\frac1{4n}\sum\limits_{k=0}^\infty \frac{(2k)!^3}{k!^4 (16n)^{2k}}}{\left(\sum\limits_{k=0}^\infty \left(\frac{n^k}{k!}\right)^2\right)^2}$$

but I have no experience in using them.

Answer 8

Hmm, I don't know whether is is actually competing. The Euler-gamma can also be seen as the "regularized" sum of all zeta's at the nonpositive integer arguments (mostly expressed in a sum-formula using the Bernoulli-numbers). If I do a convergence-acceleration-method, (in the sense of a Nörlund-matrix-summation) I get the following approximations, where the partial sums are documented in steps of 5.
$ \qquad \small \begin{array} {ll|ll} k & \text{approx partial sum to k'th term}& k & \text{approx partial sum to k'th term}\\ \hline \\ 1&1/2&6&0.576161647582377561685517908649\\ 11&0.577642454055878876964082277383&16&0.577256945328427287289300010076\\ 21&0.577203007376005733835733501905&26&0.577213676374423017168422213469\\ 31&0.577216385568992428628821604406&36&0.577215824990983093761408431095\\ 41&0.577215639855185823618977575460&46&0.577215658304198651397646593838\\ 51&0.577215664821529245660187000460&56&0.577215664719517597256388852446\\ 61&0.577215665026720261633726731324&66&0.577215664986600655216189453626\\ 71&0.577215664916609466905818220446&76&0.577215664902581218436870655519\\ 81&0.577215664899673837349687879474&86&0.577215664900634540946733895948\\ 91&0.577215664901420597291612350155&96&0.577215664901605693627171524946\\ 101&0.577215664901606197813305786106&106&0.577215664901564816031433598865\\ 111&0.577215664901542872603251577435&116&0.577215664901534551921030743308\\ 121&0.577215664901532778454660696838&126&0.577215664901532679657316339069\\ 131&0.577215664901532833003775498032&136&0.577215664901532904864265239897\\ 141&0.577215664901532914818902560099&146&0.577215664901532899695081822359\\ 151&0.577215664901532883268517660911&156&0.577215664901532871664134738564\\ 161&0.577215664901532865398778282147&166&0.577215664901532862462629396963\\ 171&0.577215664901532861321338522582&176&0.577215664901532860909786316139\\ 181&0.577215664901532860775151258773&186&0.577215664901532860715949714001\\ 191&0.577215664901532860680839731393&196&0.577215664901532860654520816630\\ 201&0.577215664901532860635577825538&206&0.577215664901532860623198773464\\ 211&0.577215664901532860615556602981&216&0.577215664901532860611334824284\\ 221&0.577215664901532860609026420469&226&0.577215664901532860607850525370\\ 231&0.577215664901532860607246781354&236&0.577215664901532860606925091229\\ 241&0.577215664901532860606758778390&246&0.577215664901532860606658539051 \\ \ldots \\ \hline &&&0.577215664901532860606512090082 \\ &&&\text{(final value as given by Pari/GP)} \end{array} $

Well, this might not compete because of the computation effort for the coefficients of the Noerlund summation and also it seems, as if the rate/quality of convergence decreases with the increasing steps, so this should possibly be seen only as a sidenote.

---

(Reminder as to how to reproduce the behaviour:

\\Pari/GP, using user-defined procedures 
NoerlundSum(1.7,1.0)*ZETA[,1]  \\matrix-function NoerlundSum and ZETA-matrix

Answer 9

I do not know about the best method, however numerically evaluating the integral $$\gamma = - \int_0^1\!dx\,\ln \ln x^{-1}$$ seems to be pretty efficient.

Answer 10

There is another interesting formula $$\small 1- \gamma = \sum_{k=2}^\infty {\zeta(k)-1\over k}$$ found in mathworld (see eq 123) .
If we simply use approximations to the zetas by truncating their series, and write this in an array
$\small \begin{array} {lll} 1 & 1 & 1 & 1 & \cdots & 1 \\ {1 \over 2^2} & {1 \over 2^3} & {1 \over 2^4} & {1 \over 2^5} & \cdots&{1 \over 2^c}\\ {1 \over 3^2} & {1 \over 3^3} & {1 \over 3^4} & {1 \over 3^5} & \cdots&{1 \over 2^c}\\ \cdots & \cdots & \cdots & \cdots & \cdots & &\\ {1 \over r^2} & {1 \over r^3} & {1 \over r^4} & {1 \over r^5} & \cdots&{1 \over r^c}\\ \hline \zeta_r(2)&\zeta_r(3)&\zeta_r(4)&\zeta_r(5)&\cdots&\zeta_r(c)& \end{array} $

then we can write an approximation-formula for the Euler $\small \gamma$ $$\small 1-\gamma_{r,c} = \sum_{k=2}^c {\zeta_r(k)-1\over k}$$ which depends on the number of rows r and the number of columns c . Now to reduce the number of coefficients needed to arrive at a good approximation

1. we can use the alternating (column-)sums and convert by the eta/zeta-conversion term

2. additionally we can use Eulersummation for convergence acceleration for the (now alternating) $\small \zeta_r(c) $

3. we can even introduce Euler-summation of (small) negative order to accelerate convergence of the sum of zetas (which itself is non-alternating).

If we use all three accelerations, we get a double sum $$\small 1-\gamma_{r,c} = \sum_{k=2}^c \sum_{j=1}^r a_{j,k}{ 1 \over j^k}$$ where the $\small a_{j,k} $ contain the factors due to the denominator in the $\small \gamma$-formula and due to the threefold convergence-acceleration.

I did actually implement this in Pari/GP and the surprising result was, that the best approximations were (using order 0.5 in the Eulersummation for the columns and -0.25 for the Eulersummation of the approximated zetas), if roughly r=c . Then the number of correct digits were about r/2; so with r=64 and c=64 we get $\small \gamma$ to 31 digits accuracy.
So the effort comes out to be $$\small \text{ # of correct digits} \sim r/2 \qquad \text{ if } r \sim c $$

The cost of computation of the complete array of zeta-terms is thus in principle quadratic in d (the required number of correct digits); for the Euler-sums a vector for the column-acceleration and another vector for the row-acceleration is required whose values can recursively be computed and are thus linear with the number of rows resp the number of columns and thus also linear with d. (The convergence-acceleration (1.) by using the alternating sums costs nearly nothing)

Answer 11

I found this 2013 paper claiming to offer the first general continued fraction for $\gamma$ with regular pattern. It has almost exponential convergence. The $\log_{10}$ of absolute error is plotted below:

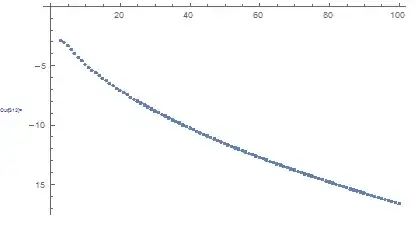
The error is of the order of $10^{-17}$ at $100$ steps of the algorithm.

The continued fraction it creates is a little bit complicated, starting with several terms having no apparent pattern:

$$\gamma=\cfrac{1}{2-\cfrac{1}{4-\cfrac{5}{16+\cfrac{36}{59-\cfrac{15740}{404-\cfrac{1489700}{30422-...}}}}}}$$

The next partial quotents grow very fast in absolute value.

The computation of partial quotents after $5$ is based on a complicated three order reccurence relation, which is described in details in the paper on page 14.

First, we define:

$$q_n=\sum^{n}_{k=0} \left( \begin{matrix} n \\ k \end{matrix} \right)^2 k!$$

Then we define the few initial values $d_1=-1$, $d_2=-2$, $d_3=-5$, $d_4=8$ for a $3^{rd}$ oder reccurence relation for $n \geq 3$:

$$(n-1)(n-2)d_{n+2}=$$

$$=(n-2)(n+1)(n^2+3n-2)d_{n+1}-n^2(2n^3+n^2-7n-4)d_n+n^4(n-1)^2d_{n-1}$$

Then the partial quotents $\frac{a_n|}{|b_n}$ will be defined for $n \geq 6$ as:

$$a_n=-\frac{(n-1)^2}{4}d_n d_{n-2}$$

$$b_n=n^2 d_{n-1}+\frac{(n-1)(n-2)}{2}q_{n-2}$$

Here is my implementation in Mathematica.

A0 = {{0, 1}, {1, 0}};
Af = {{1}, {0}};
Nm = 100;
q = Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]\(
\*SuperscriptBox[\(Binomial[n, k]\), \(2\)]\ \(k!\)\)\), {n, 1, Nm}];
d = Table[0, {n, 1, Nm}];
d[[1]] = -1;
d[[2]] = -2;
d[[3]] = -5;
d[[4]] = 8;
Do[d[[n + 2]] = ((n + 1) (n^2 + 3 n - 2) d[[n + 1]])/(n - 1) - (
n^2 (2 n^3 + n^2 - 7 n - 4) d[[n]])/((n - 1) (n - 2)) + 
n^4 (n - 1)/(n - 2) d[[n - 1]], {n, 3, Nm - 2}];
a = Table[0, {n, 1, Nm}];
b = Table[0, {n, 1, Nm}];
b[[1]] = 2;
b[[2]] = 4;
b[[3]] = 16;
b[[4]] = 59;
b[[5]] = 404;
a[[1]] = 1;
a[[2]] = -1;
a[[3]] = -5;
a[[4]] = 36;
a[[5]] = -15740;
Do[a[[n]] = 1/4 (-(n - 1)^2) d[[n]] d[[n - 2]]; 
b[[n]] = n^2 d[[n - 1]] + 1/2 (n - 1) (n - 2) q[[n - 2]], {n, 6, 
Nm}];
er = Table[0, {n, 1, Nm}];
Do[A1 = {{b[[n]], 1}, {a[[n]], 0}};
P0 = A0.Af;
A0 = A0.A1;
P = A0.Af;
Pf = N[P[[1, 1]]/P[[2, 1]], 20];
er[[n]] = Log[10, Pf - EulerGamma];
Print[n, " ", Pf, " ", Pf - EulerGamma], {n, 1, Nm}]
ListPlot[er]

1 arXiv:1010.1420 [math.NT]

Answer 12

No heavy machinery or special series manipulation required for this. Simple enough to do on a standard scientific calculator.

By applying the Euler-Maclaurin summation formula, one finds that

$$\lim_{b\to\infty}H_b-H_{n-1}-\ln(b)+\ln(n)=\frac1{2n}+\left(\sum_{j=1}^p\frac{B_{2j}}{2j\times n^{2j}}\right)+R_{n,p}$$

and thus, we may derive

$$\gamma=H_{n-1}-\ln(n)+\frac1{2n}+\left(\sum_{j=1}^p\frac{B_{2j}}{2j\times n^{2j}}\right)+R_{n,p}$$

where

$$H_n=\sum_{k=1}^n\frac1k$$

$$|R_{n,p}|\le\frac{2\zeta(2p)(2p-1)!}{(2\pi n)^{2p}}$$

where $\zeta$ is the Riemann zeta function. It suffices to use

$$\zeta(s)<\frac1{1-2^{1-s}}\left(1-\frac1{2^s}\right)$$

Or more simply,

$$\zeta(s)<2$$

both for $s\ge2$.

For example, with $n=5$ and $p=4$, we can approximate out $7$ places:

$$\gamma=H_4-\ln(5)+\frac1{10}+\frac1{300}-\frac1{75000}+\frac1{3937500}-\frac1{93750000}+R_{5,4}$$

$$\gamma\approx0.577215664+R_{5,4}$$

where

$$|R_{5,4}|<1.1\times10^{-8}$$