How to find center of a conic section from the equation?

Question

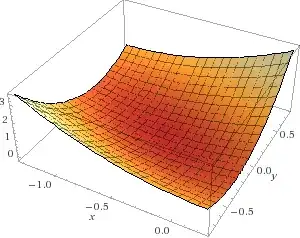
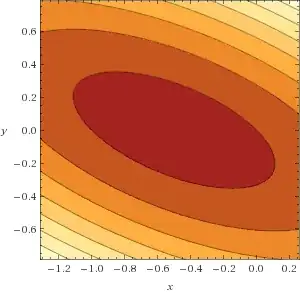
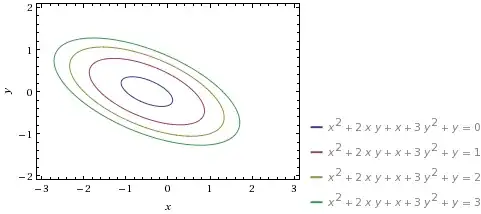
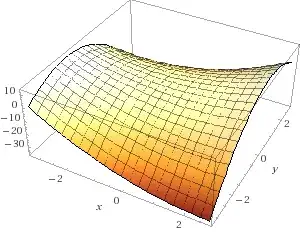
If we are given a curve in the form $$ax^2+2bxy+cy^2+2dx+2ey+f=0$$ and the following determinant $$\delta=\begin{vmatrix}a&b\\b&c\end{vmatrix}=ac-b^2$$ is non-zero, then this is either a curve of elliptic type (an ellipse, a point or an empty set/an imaginary ellipse) or a curve of hyperbolic type (a hyperbola or a pair of lines). So in these cases in makes sense to talk about center of the curve, i.e., the point with respect to which this curve is symmetric.

The center can be found as the solution of the following system of equations $$\begin{align*} ax+by+d&=0,\\ bx+cy+e&=0. \end{align*}$$ (This system has a unique solution, since the determinant of the matrix of this system is $\delta\ne0$.)

That means, the coordinates of the center can be computed as $$\begin{align*} x&=\frac{be-cd}\delta,\\ y&=\frac{bd-ae}\delta. \end{align*}$$

Several resources can be found where this way of finding center is described. (Often in the form of solving $\frac{\partial F}{\partial x}= \frac{\partial F}{\partial y} =0$, where $F(x,y)=ax^2+2bxy+cy^2+2dx+2ey+f$.)

How can these conditions for the center be derived? How can we show that the point fulfilling these equation indeed is the center of the conic section?

Answer 1

Matrix derivation

The original equation can be described in a more concise form as $$\vec x A \vec x^T + \vec x \vec b^T + \vec b \vec x^T + f =0$$ or $$\vec x A \vec x^T + 2\vec x \vec b^T + f =0$$ where $\vec b=(d,e)$ and $A=\begin{pmatrix}a&b\\b&c\end{pmatrix}$.

If the vector $\vec x_0$ represents the center then in a coordinate system with the origin in this point the equation will be $$(\vec x-\vec x_0) A (\vec x-\vec x_0)^T + g =0$$ which can be rewritten as $$\vec x A \vec x^T - 2\vec x A\vec x_0^T + \vec x_0 A \vec x_0^T +g.$$

Which means the we need to choose $\vec x_0$ in such way that $-2A\vec x_0^T=2\vec b^T$, i.e. $$A\vec x_0^T=-\vec b^T,$$ $$\begin{pmatrix}a&b\\b&c\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}= \begin{pmatrix}d\\e\end{pmatrix}.$$

This is precisely the following system of linear equations written in the matrix form: $$ \begin{align*} ax + by &= -d\\ bx + cy &= -e \end{align*} $$

(To give credit where credit is due, I was shown this derivation by a colleague of mine who taught labs for the same subject as I did, but with another group of students.)

---

Derivatives

We can view the curve as a level set of the function $$F(x,y)=ax^2+2bxy+cy^2+2dx+2ey.$$ The level sets of this function create the family of curves $ax^2+2bxy+cy^2+2dx+2ey+f=0$, where the parameter $f$ is changing.

For example, if $\delta>0$ we get concentric ellipses, like in this example - the plots are taken from WolframAlpha:

And a different plot:

If $\delta>0$, we get a family of hyperbolas. WolframAlpha:

And a different plot:

In the first case, the function $F$ has minimum at the center of each of the ellipse. In the second case there is a saddle point. In both cases, the center fulfills $$\frac{\partial F}{\partial x}= \frac{\partial F}{\partial y} =0$$ which leads to the system of equations \begin{align*} ax + by +d&= 0\\ bx + cy +e&= 0 \end{align*} which is precisely the linear system described above.

So far we have only drawn some pictures (which is good for intuition, but picture is not a proof.) If we want to give a more rigorous reason why this works we can use some known facts about quadratic forms. We know from Principal axis theorem that there is a rotation and translation such that in the new coordinates the curve has $$\lambda_1 x^2 + \lambda_2 x^2=const$$ Clearly $F(x,y)=\lambda_1 x^2 + \lambda_2 x^2$ has partial derivatives equal to zero at the origin. (And depending on the signs of $\lambda_{1,2}$ we can say whether it has minimum, maximum or saddle point there.)

Answer 2

I would emphasize that a pure translation in the plane preserves the relationship between a figure and its center. Given $$ A x^2 + 2 B xy + C y^2 + 2 D x + 2 E y + F = 0 $$ and solving for $(x_0, y_0)$ in $$ A x_0 + B y_0 + D = 0, $$ $$ B x_0 + C y_0 + E = 0, $$ we introduce translated coordinates $(u,v)$ with $$ x = u + x_0, $$ $$ y = v + y_0. $$ I'm not sure how much I will type in, but the original equation

$$ A x^2 + 2 B xy + C y^2 + 2 D x + 2 E y + F = 0 $$ becomes $$ A u^2 + 2 B uv + C v^2 = \rm{constant.} $$ Regardless of what type of figure this might be, it is centrally symmetric in $(u,v)$ coordinates: if $(u,v)$ is a solution, so is $(-u,-v).$

APPENDIX:

$$ A x^2 + 2 B xy + C y^2 + 2 D x + 2 E y + F = 0. $$

$$ x = u + x_0 $$ $$ y = v + y_0 $$

$$ x^2 = u^2 + 2 x_0 u + x_0^2 $$ $$ xy = uv + y_0 u + x_0 v + x_0 y_0 $$ $$ y^2 = v^2 + 2 y_0 v + y_0^2 $$

$$ A x^2 + 2 B xy + C y^2 = (A u^2 + 2B uv + C v^2) + (2Ax_0 + 2 B y_0) u + (2Bx_0 + 2 C y_0) v + (Ax_0^2 + 2B x_0 y_0 + C y_0^2) $$ $$ 2 D x + 2 E y + F = 2 D u + 2 E v + 2 D x_0 + 2 E y_0 + F $$ In the original $A x^2 + 2 B xy + C y^2 + 2 D x + 2 E y + F,$ the quadratic terms come out to $A u^2 + 2B uv + C v^2,$ as was guaranteed to happen for the highest degree terms. Next, we get $ (2Ax_0 + 2 B y_0 + 2 D)u, $ so that the coefficient of the linear term $u$ is actually $0.$ Also, $ (2Bx_0 + 2 C y_0 + 2 E)v , $ so that the coefficient of the linear term $u$ is actually $0.$ The constant term comes out to $$ Ax_0^2 + 2B x_0 y_0 + C y_0^2 + 2 D x_0 + 2 E y_0 + F $$ to which we say, Why Not? The whole thing is now $$ A u^2 + 2B uv + C v^2 + ( Ax_0^2 + 2B x_0 y_0 + C y_0^2 + 2 D x_0 + 2 E y_0 + F) = 0, $$ where the thing in parentheses is a constant. Let us give the constant a name, $ W = ( Ax_0^2 + 2B x_0 y_0 + C y_0^2 + 2 D x_0 + 2 E y_0 + F). $ So we get $$ A u^2 + 2B uv + C v^2 + W = 0 $$

Answer 3

At the risk of sounding grumpy, I don't unless I have to.

I try to write my conic sections in the closest form to a description of its properties I can get away with. I don't try to understand conic properties as a result of cartesian coordinates, because that's backward. I do keep track of what methods are necessary to distinguish and retrieve properties from a faceless abstraction like homogeneous coordinates, so that I can spend as little time as possible working backward.

The cartesian form is unsuitable for many common tasks such as anything that requires an oriented figure. It's clumsy for moving, rigid figures. I prefer a form I can read, that doesn't lose track of the properties in the first place.

Consider at least one alternative. Following Apollonius, we can always write (one branch of) a conic section in the form

${\bf \vec f}(t) =P + t \sqrt{c_1 + c_2 t^2}\, {\bf \vec x} +t^2 {\bf \vec y}$

where P is any point on the section, x is tangent to the curve at P (the ordinate direction), and y gives the diameter direction. We may choose any lengths and directions for the vectors. Specifically, we define the conic by choosing any ordinate chord to the diameter with base point P.

I leave it to you to identify
1. why this is so, and to explain
2. why it is equivalent to the general second-order Bezier section (conic section from two points, the intersection of the tangents at those points, and a free parameter, $ 0<\lambda <1$ indicating the elevation of the curve above the base of the triangle.)
3. the relationship between c1, c2, and $ \lambda$. (Hint: the shape of a conic section is a single parameter).
4. the center of the section, if any.
5. the (major) axis.

hehehe. Just kidding. Friends don't leave friends alone with abstractions. If you want to know, I can tell you how I have gone about the construction until you are satisfied. We have got the wrong side of an abstraction when we get to asking "why?" from the blind end of the puzzle instead of examining whether and how measure is preserved by the construction of the abstraction in the first place. To do this, we must have an independent reference. Here, it is the figures themselves. Suppose, for example, we knew nothing about conic sections. How would you describe the relationship of the standard form to the act of measuring distances and directions on the surface of a flat cut through a cone?

Hmmmm?