Is it a valid to say $$ {n \choose k} = \Theta \left( n^k \right) $$ for any $n$ and $k$? If so, how to prove it?
Note: $k$ is not a function of $n$.
Note: Observed it here (page 5): http://www.cs.berkeley.edu/~sinclair/cs271/n6.pdf
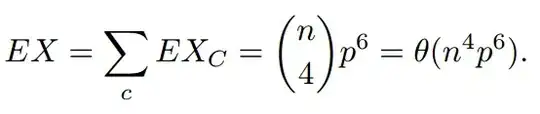
Is it a valid to say $$ {n \choose k} = \Theta \left( n^k \right) $$ for any $n$ and $k$? If so, how to prove it?
Note: $k$ is not a function of $n$.
Note: Observed it here (page 5): http://www.cs.berkeley.edu/~sinclair/cs271/n6.pdf
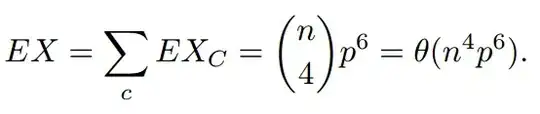
You have that $$ \binom{n}{k} = \frac{n!}{(n-k)!k!} = \frac{1}{k!}\frac{n!}{(n-k)!} = \frac{1}{k!}\left(n(n-1)(n-2)\dots(n-k+1)\right). $$ As far as the $\Theta(\cdot)$ notation is concerned, $k$ is a constant, so $\frac{1}{k!}=\Theta(1)$, and $$ \left(n(n-1)(n-2)\dots(n-k+1)\right) = n^k\cdot\left(1\left(1-\frac1n\right)\left(1-\frac2n\right)\dots\left(1-\frac kn\right)\right) $$ and as $k$ is fixed,, $$ \left(1\left(1-\frac1n\right)\left(1-\frac2n\right)\dots\left(1-\frac kn\right)\right) \xrightarrow[n\to\infty]{} 1 $$ so that indeed $$ \binom{n}{k} = \Theta(n^k) $$
We can even make a stronger statement that $${n \choose k} = O\left (\left( \frac{e \cdot n}{k} \right)^k \right)$$ For the proof, see this.
The time complexity of calculating the binomial coefficient C(n, k) can be expressed in different ways, depending on the algorithm used. The most common methods to calculate C(n, k) include:
Direct Calculation: The straightforward method is to use the binomial coefficient formula:
C(n, k) = n! / (k! * (n - k)!),
Calculating factorials has a time complexity of O(n), so the time complexity for calculating C(n, k) using this formula is O(n) (or Θ(n)).
Dynamic Programming: Another common approach is to use dynamic programming to calculate C(n, k) more efficiently. This is typically done using a 2D array to store intermediate results and has a time complexity of O(n * k) (or Θ(n*k)).
Pascal's Triangle: If you have precomputed Pascal's triangle or a memoization table, you can look up the value of C(n, k) in constant time. Building Pascal's triangle requires O(n^2) time, but once it's constructed, accessing values is O(1).
A short message to Clement C and IY3:
In the context of the binomial coefficient (n choose k), it is indeed correct to say that (n choose k) is Θ(n^k). The reason for this is that (n choose k) is a polynomial function of degree k in n. In Big O notation (Θ notation), we look for upper bounds or tight bounds on the growth of a function. In this case, the growth of (n choose k) is proportional to n^k, so we can represent it as Θ(n^k).
Your initial logic is valid, but you made it more complicated than it needed to be. (n choose k) is indeed Θ(n^k) because it's a polynomial function of n with degree k. The constants involved in k! and other terms do not change the overall polynomial nature of the function. But as I mentioned above, it can be of Θ(n) or Θ(n*k).