Why does $(A/I)\otimes_R (B/J)\cong(A\otimes_R B)/(I\otimes_R 1+1\otimes_R J)$?

Question

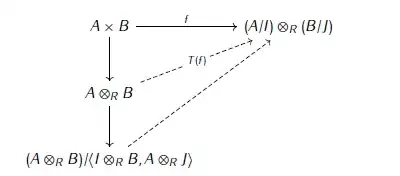
While reading, there is an isomorphism that I'm having trouble fulling seeing.

If you have two algebras $A$ and $B$ over a commutative ring $R$, with $I$ and $J$ two sided ideals in $A$ and $B$, then you should have an isomorphism $$ (A/I)\otimes (B/J)\cong (A\otimes B)/(I\otimes 1+1\otimes J). $$

Now there are bilinear maps from $A/I\times B/J\to (A\times B)/(I+J)$ and so the universal property of the tensor product gives unique maps $(A/I)\otimes (B/J)\to (A\times B)/(I+J)$. Does this somehow get to the isomorphism above, or am I completely off track? What is the quick way to see this? Thanks!

Answer 1

By the universal properties of quotient algebras, tensor products ( = coproducts of algebras), we have for every $R$-algebra $T$:

$\hom(A/I \otimes B/J,T) \cong \hom(A/I,T) \times \hom(B/J,T)$

$\cong \{f \in \hom(A,T),g \in \hom(B,T) : f|_I = 0, g|_J = 0\}$

$\cong \{h \in \hom(A \otimes_R B,T) : f:=h(- \otimes 1), g:=h(1 \otimes -) \text{ satisfy } f|_I = 0,~ g|_J = 0\}$

$\cong \{h \in \hom(A \otimes_R B,T) : h|_{I \otimes 1 + 1 \otimes J}=0\}$

$\cong \hom((A \otimes_R B)/(I \otimes 1 + 1 \otimes J),T)$

By the Yoneda lemma, we are done.

Remark: This is one of the thousands of trivial isomorphisms in basic algebra which are usually proved (in textbooks, lectures, etc.) in a too complicated way. Instead, you can always just use the Yoneda lemma and the involved universal properties. And then there is nothing to do at all ... By the way, this abstract approach is the only one which is applicable in more abstract contexts, where you can't use elements anyway.

Answer 2

Let's solve your problem in two steps:

Step 1
Consider the exact sequence of $R$-modules $0\to I\to A\to A/I \to 0$ .
Tensoring with $B$ and remembering that tensoring is right exact we obtain
the exact sequence $I\otimes_R B \to A\otimes_R B\to A/I\otimes_R B\to 0$.
Writing $I^e$ for the image of $I\otimes_R B \to A\otimes_R B \;$ [the exponent e in $I^e$ stands for "extension of ideal $I$ to ring $A\otimes_R B $" ] we get the identification of $R$-algebras $$A/I\otimes_R B\cong (A \otimes_R B)/I^e:\bar a\otimes b \mapsto \overline {a \otimes b} \quad (*)$$

Step 2
Applying the corresponding result in Step 1 to the right hand side of the tensor product we get $$A/I\otimes_R B/J\cong (A/I\otimes_R B)/J^e \quad (**)$$
Applying Step 1 again, we replace $A/I\otimes_R B$ in $(**)$ by $(A\otimes_R B)/I^e$ and get
$$(A/I\otimes_R B)/J^e \cong \frac {(A\otimes_R B)/I^e}{I^e+J^e/I^e} \quad (***)$$ where the ideal $I^e +J^e$ , denoted $I\otimes 1+1\otimes J$ in Danielle's question, is the subgroup of $A\otimes_R B$ generated by elements of the form $i\otimes b+a\otimes j$ where $i\in I, b\in B, j\in J,\, a\in A$

Conclusion
Finally thanks to Noether we obtain from $(**)$ and $(***) $ the required final identification of $R$-algebras : $$ A/I\otimes_R B/J\cong (A\otimes_R B)/(I^e +J^e):\bar a\otimes \bar b\mapsto \overline {a\otimes b} \quad (****) $$

Answer 3

Think about $$ A\times B \rightarrow A/I \otimes B/J \quad\text{induced from}\quad A \times B \rightarrow A/J \quad \text{and} \quad A\times B \rightarrow B/J $$ giving you a homomorphism $$ \Phi:A \otimes B \rightarrow A/I \otimes B/J \quad \Phi(a\otimes b)=(a+I)\otimes(b+J) $$ It is obvious that $I\otimes 1 \subseteq \operatorname{Ker}\Phi$ and $1\otimes J \subseteq \operatorname{Ker}\Phi$ so their sum is also in the kernel. It remains to show that the sum is the kernel.

Note that $I\otimes 1$ is the ideal generated by $f(I)$ for $f:A\rightarrow A\otimes B$ and $1\otimes J$ is the ideal generated by $g(J)$ for $g:B \rightarrow A\otimes B$. Then there are homomorphisms $$ A/I \rightarrow A\otimes B/(f(I)+g(J)) \quad \text{and} \quad B/J \rightarrow A\otimes B/(f(I)+g(J)) $$ and hence $$ A/I \otimes B/J \rightarrow A\otimes B/(f(I)+g(J)) \rightarrow A\otimes B/\operatorname{Ker}(\Phi) \rightarrow A/I \otimes B/J $$ Can you show that $f^{-1}(f(I)+g(J))=I$ and $g^{-1}(f(I)+g(J))=J$?

Answer 4

The quick way to see this is to just write down the isomorphism. In this case it's "obvious": it sends $a \otimes b$ to $a \otimes b$. You just need to check it and its inverse are well-defined.

As to your approach, first what do you actually mean by $(A \times B)/(I + J)$? Was that supposed to be $I \times B + A \times J$? Or maybe $I \times 0 + 0 \times J$ or even $I \times J$?

You are off track a bit -- whatever you mean by the target space, the map $A/I\times B/J\to (A\times B)/(I+J)$ is going to be linear, not bilinear. I'm sure your idea will work once you sort out what it is you have and what you actually need to show. (but it will be a bit messy, I imagine)

EDIT: Now that I've thought about, it's not so messy if you organize it right. The way I thought of it, the first step is to realize:

• A homomorphism $(A \otimes B) / (I \otimes 1 + 1 \otimes J) \to C$

is the "same" thing as

• A homomorphism $\phi: A \otimes B\to C$ with $\phi(i \otimes 1) = \phi(1 \otimes j) = 0$

which is the "same" thing as

• A bilinear map $\phi : A \times B \to C$ with $\phi(i,1) = \phi(1,j) = 0$

which is....

Answer 5

A direct proof of this fact.

Define the map $g\colon (A/I)\times (B/J)\longrightarrow (A\otimes_R B)/\langle I\otimes_R B, A\otimes_R J\rangle$ by $g(a+I,b+J)=a\otimes_R b+\langle I\otimes_R B, A\otimes_R J\rangle$.

Of course $g$ is well-defined and $R$-bilinear, therefore we have, by universal proprerty of the tensor product, an induced homomorphism $T(g)$.

(Notice that $(A\times B)/(I\times J)\approx (A/I)\times (B/J)$). We claim that $g$ is the wanted isomorphism. As done above, we define an inverse of $g$. To do this it's enough to use the universal proprerty of the tensor product and that of the quotient.

Here $f\colon A\times B\longrightarrow (A/I)\otimes_R (B/J)$ is defined by $f(a,b):= (a+I)\otimes_R(b+J)$.