How would one express a solution to $\sqrt{x} =-1$?
I just read that a solution to the above equation cannot be expressed in the form of complex numbers, really interested in any additional information I could learn about this!
Thank you to anyone who helps in advance.
Mathematicians are often pedantic--"What do you mean by $\sqrt{\phantom{x}}$?" "What are the domain and target of this function?"--but the question "How to express (solutions of) $\sqrt{x} = -1$?" is a prime example of the need to be grindingly specific about the meaning of symbols.
As user46944 and Alizter point out, if $x$ is real and non-negative, then "$\sqrt{x}$" conventionally refers to the unique non-negative square root of $x$. That is, $\sqrt{\phantom{x}}:[0, \infty) \to [0, \infty)$ is a function.
With this understanding, the equation $\sqrt{x} = -1$ has no (real, non-negative) solution, even though squaring both sides yields the equation $x = (\sqrt{x})^{2} = (-1)^{2} = 1$, which has $x = 1$ as a solution. (Incidentally, in this setting, the equation "$(\sqrt{x})^{2} = x$ only makes sense for non-negative real $x$.)
What if we want to take complex square roots? Numerous questions at Math.SE address this; the following is taken verbatim from an answer to this question:
If by the radical symbol you mean the set-valued function that associates to each non-zero complex number $w$ the two complex numbers $z$ satisfying $w = z^{2}$, and if "squaring a set $A$" means "the set obtained by squaring each element of $A$", then for each complex $z$,
$\sqrt{z^{2}} = \{\pm z\}$ by the difference of squares identity: For complex numbers $z_{1}$ and $z_{2}$, you have $z_{1}^{2} = z_{2}^{2}$ if and only if $z_{1} = \pm z_{2}$.
$(\sqrt{z})^{2} = \{z\}$ from the definitions of $\sqrt{\phantom{z}}$ and squaring a set.
In this setting, "$\sqrt{x} = -1$" still has no solution (there is no complex number whose unique square root is $-1$), but we do have $\sqrt{1} = \{-1, 1\}$.
But perhaps allowing multi-valued square roots feels like cheating. Unfortunately, matters become problematic if we require a (single-valued) square root function. The essential problem is topological, not algebraic: Every non-zero complex number has precisely two complex square roots, differing by a sign, and there is no "continuous choice of square root".
More formally, there does not exist a continuous, complex-valued function $\sqrt{\phantom{z}}$ defined on the set of non-zero complex numbers and satisfying $(\sqrt{z})^{2} = z$ for all non-zero $z$.
The diagram below explains why: If we start with the non-negative real square root on the non-negative real axis, then attempt to extend by continuity (the gray shaded surface), we "arrive at the negative square root" after one traversal of a circle around the origin.
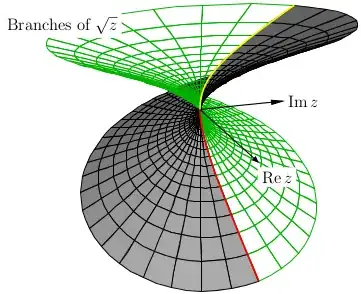
(The entirety of the diagram, the solid gray sheet together with the green mesh, may be viewed as the real part of the "set-valued" square root described above.)
Unlike the situation for square roots of non-negative real numbers (where the "natural" domain was the set $[0, \infty)$ of non-negative reals), there is no natural domain for a continuous complex square root function. Often one removes the non-positive reals; sometimes removing the negative imaginaries (and zero) is preferable.
Further, if $\sqrt{\phantom{z}}$ denotes an arbitrary continuous branch of the complex square root, the equation "$\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}$" fails to hold for some $a$ and $b$. Bother.
Though one can make a case that "$z = 1$ is a solution of $\sqrt{z} = -1$" (by choosing a branch of square root that takes the value $-1$ at $z = 1$!), that's asking for trouble. When people see a radical sign signifying a square root, one of the first expectations is that the value is non-negative if the radicand is a non-negative real number.
The problem with the equation isn't as mysterious as you might think. When we take the square root of any number, if the square root is a real number, it is positive. For example, $\sqrt{4} = 2$. A lot of people think that $\sqrt{4} = \pm 2$ since "well, you are getting the number that, when squared, gives you 4".
But actually, what they are describing is the solution to the equation $x^{2} = 4$. To find the solution to this equation, you ask yourself for the numbers that, when squared, give you $4$. And these numbers are $\pm \sqrt{4}$. Notice that $\sqrt{4}$ here is always positive. But we tack on a negative when expressing that part of the solution of $x^{2} = 4$. So, $\sqrt{4}$ is not $\pm 2$. It's just $2$. While $-\sqrt{4} = -2$.
Thus, when we say $\sqrt{x} = -1$, we are saying that something positive on the left hand side equals something negative on the right hand side. And you know this can't happen unless both sides are $0$, which one isn't.
Let $x=a+bi$ then $\sqrt{x}=\sqrt{a+bi}=-1$. Then square both sides to get $a+bi=1$. Thus $x$ must be a 'real' number and not complex. Now if $a=1$, taking the positive square root, which is what $\sqrt{.}$ means, will give you that $\sqrt{1}=-1$. Which is not strictly true when using the radical sign.
You can however consider the solutions to the equation $x^2-1=0$ and define the square root(s) of a number $c$ to be the solutions to $x^2-c=0$.
When working with the real numbers, we had the convenience of not always having to consider the negative solutions for a result to make sense. This is not strictly true in the complex numbers, therefore operations like taking square roots must be more precisely defined and hence it must be taken into account that such an operation can have multiple results.
So the equation can't have a solution.
– Kitegi Apr 02 '15 at 11:43