According to my logic,
$$\large\sqrt{x^2} = x^{2\times \frac{1}{2}} = x = x^{\frac{1}{2}\times 2}={(\sqrt{x})}^2$$
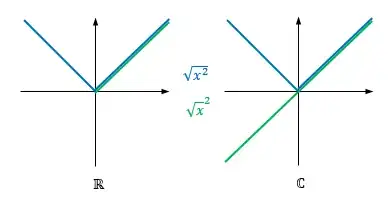
But when I look at the graphs of these guys, they're totally different.
Edit: Complex answers are okay, if you know what I mean.
According to my logic,
$$\large\sqrt{x^2} = x^{2\times \frac{1}{2}} = x = x^{\frac{1}{2}\times 2}={(\sqrt{x})}^2$$
But when I look at the graphs of these guys, they're totally different.
Edit: Complex answers are okay, if you know what I mean.
$f(x)=\sqrt{x^2}=|x|,$ so if $x\ge 0$, then $f(x)=x$. And if $x\lt 0$, then $f(x)=-x.$
On the other hand, $g(x)={\sqrt x}^2=x$ is defined only when $x\ge0.$
Hence, we know that $y=f(x)=\sqrt{x^2}$ is different from $y=g(x)={\sqrt x}^2.$
Since noone has (yet) pointed out where your logic went wrong,
the expression $a^b$ is not always well-defined : usually you need $b$ to be an integer or $a$ to be a positive real for it to make sense (also you need $b \ge 0$ if $a=0$) (you can define it in more cases but it is complicated enough like this)
So the identity $(a^b)^c = a^{bc}$ is often nonsense because it talks about things that don't exist or they both exist but are not the same. However it is true when $a$ is positive or if both $b$ and $c$ are integers (and surely in some other complicated cases)
In your case $(x^\frac 12)^2$ is only well-defined for positive $x$ and for those $x$ we do have $(x^\frac 12)^2 = x^1$, while $x^1 = (x^2)^\frac 12$ for positive $x$ and not for negative $x$.
Notice that:
$$\sqrt{x^2} = |x|$$
And
$$\sqrt{x}^2 = x$$
But also notice that the domains are different:
$$\sqrt{x^2}: (-\infty, \infty)$$
And
$$\sqrt{x}^2 = [0, \infty)$$
Make sense now why the graphs would look different?
I think your confusion arrises from the idea that the $\sqrt{\cdot}$-fuction is the inverse function of $\cdot^2$. This is not exactly the case; you see $f(x)=x^2 $ does not really allow for an inverse function, because you can always find two distinct values $a_1$ and $a_2$ such that $(a_1)^2=(a_2)^2=x$ (exept maybe for the $0$-case). So there is in fact no "good" reason why we should have $$\sqrt{x^2}=\sqrt{x}^2,$$ because this kind of behaviour is something you would generally expect from functions and their inverse. And since $\sqrt{\cdot}$ is not a proper inverse function for $\cdot^2$ we should not be supprised that in general $\sqrt{x^2}\neq\sqrt x^2$.
For a more elaborate discussion on functions and their inverses, see this.
I think you want an answer allowing for the case of imaginary numbers.
Your are under the impression (under your logic) that $f\circ g(x) = g\circ f(x)$.
This is clearly not true in general, and not true in your case, even if, at first sight, case, $g$ is similar to the inverse of $f$.
But $g$ is NOT the inverse of $f$, for $f$ does not have any inverse, since $x^2$ is not injective, be it in real or imaginary fields...
Your equation reminds me of the following: Gift $=$ Present. It looks truthful, doesn't it ? But is it always ? Well, if both words are taken to be written in English, even then there's a glitch, since the second one has at least two completely different meanings, so, depending on its interpretation, the equation can be either true or false. But what if the two words are actually an entry in a German-English dictionary, instead of being one from an English thesaurus, as we previously suspected ? Then the equation is false, since the German word Gift means poison$(!)$. Now, a language is for a word what a domain of definition is to a function. So, what is the definition domain of your square root function ? If this domain is $\mathbb R^{^\mathbf+}$ then your equation is indeed true. And if not, then, as it has already been pointed out in the comment section, for $x\in$ R we have $\sqrt{x^2}=|x|$, and $\big(\sqrt x\big)^2=x$. For instance, $\sqrt{(-1)^2}=\sqrt1=1$, but $\Big(\sqrt{-1}\Big)^2=\big(\pm i\big)^2=-1$.
$\large\sqrt{x^2}$ the domain of it is $(-\infty,+\infty)$ because $x^2\ge0$ always,so $x \in $$ (-\infty,+\infty)$ and the range of the function is $[0,+\infty)$ since square root function always produces non-negative result(i.e., $\ge 0$) whereas,
${(\sqrt{x})}^2$ the domain of it is $[0,+\infty)$ since square root function accept only positive values including zero($\ge0$) and the range of it is $[0,+\infty)$ since square of any number is greater than zero($\ge0$)
If by the radical symbol you mean the set-valued function that associates to each non-zero complex number $w$ the two complex numbers $z$ satisfying $w = z^{2}$, and if "squaring a set $A$" means "the set obtained by squaring each element of $A$", then for each complex $z$,
$\sqrt{z^{2}} = \{\pm z\}$ by the difference of squares identity: For complex numbers $z_{1}$ and $z_{2}$, you have $z_{1}^{2} = z_{2}^{2}$ if and only if $z_{1} = \pm z_{2}$.
$(\sqrt{z})^{2} = \{z\}$ from the definitions of $\sqrt{\phantom{z}}$ and squaring a set.
In real numbers, square roots are defined for non-negative numbers only, and $$\sqrt{x^2}=\left(\sqrt x\right)^2.$$
In complex numbers, the principal square root can be defined to have its argument in $(-\frac\pi2,\frac\pi2]$, and for negative numbers, $\sqrt{x^2}=|x|=-x$, $\sqrt x^2=(i\sqrt{|x|})^2=-|x|=x$, so that $$\sqrt{x^2}=-(\sqrt x)^2.$$