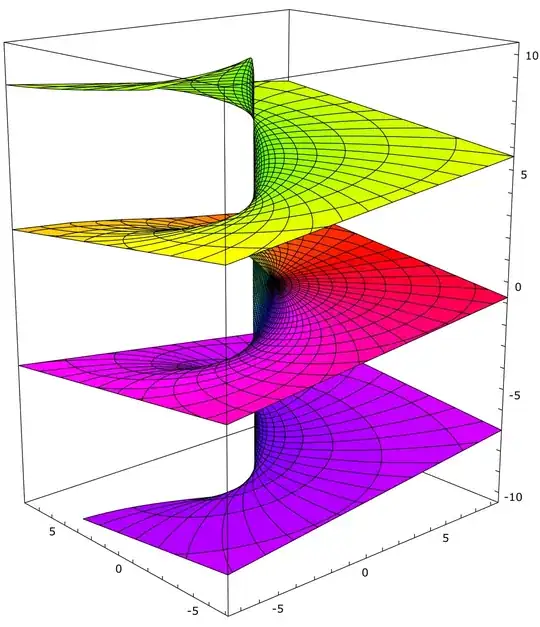
I have been scouring the internet trying to figure out how Riemann surfaces work, and I found two different explanations of them. The first visualizing the surface by plotting the real part(or imaginary) of the function defined over $\mathbb{C}$ as the height above the plane and the second involves a procedure of gluing sheets
The gluing planes, I find it difficult to explain the idea in generality, but I will try with the example for $w=\log z = \log r + i \theta$, we know that each time spin about the a circle in the input plane, we get a different value of $\omega$. Eg:
$$ w(re^{i\theta}) = \log r + i (\theta)$$
$$ w ( re^{i \theta + 2 \pi} = r e^{i \theta} ) = \log r + i ( \theta + 2 \pi)$$
Now to fix this issue of the same input point giving multiple value, we take two copy of $Z$ plane, and cut a line from origin (the branch point) to infinity. One each sheet we have an edge above the cut and below the cut. Join the the bottom edge of the first sheet with the top edge of the second sheet, repeat this iteratively , we get the Riemann surface which is suppose to represent the true domain of $\log z$
The second construction makes more sense to make because it should be that we can embed in the Riemann surface into 3D as it's fundamentally a two dimensional surface ( requires only two parameters to describe $(r, \theta) $).
Returning to the question: How exactly is this second construction of sheet gluing related to the first construction involving plotting the real part as height above plane? What advantage does the first have over the second?
BTW I will appreciate resources/ references to understanding Riemann surfaces in comments. Here are some things I found helpful:
- Reading Feynman Blog
- Roger Penrose Road to Reality (Yes the book has a chapter just for this which explains the actual philosophy behind Riemann surfaces)
- Berkeley mathematician's explanation of Riemann surfaces (I don't fully understand this as the language in it is beyond the level of rigour I currently can understand)