What math statement with proof do you find most beautiful and elegant, where such is accessible to a general audience, meaning you could state, prove, and explain it to a general audience in roughly $5 \pm\epsilon$ minutes. Let's define 'general audience' as approximately an average adult with education and experience comparable to someone holding a bachelor's degree in any non science major (e.g. history) from an average North American university.
-
39"If there are $\omega$ supercompact cardinals, then it is consistent that $\aleph_{\omega+1}$ has the tree property." :-) – Asaf Karagila Jan 17 '15 at 23:24
-
12I would recommend watching numberphile on youtube, he has a lot of videos that would be appropriate answers to this question. – DanielV Jan 17 '15 at 23:38
-
1Kelly's proof of Sylvester-Gallai Theorem may be an example. – Jan 18 '15 at 06:46
-
4If you wanted an inaccessible proof of an accessible fact to a general audience, I'd suggest the proof of the fact that the shortest path between two points is a straight line... – user541686 Jan 23 '15 at 23:35
-
4@AsafKaragila, what does that even mean? – dfeuer Jan 26 '15 at 02:42
-
@dfeuer: We say that a cardinal $\kappa$ has the tree property if every tree of height $\kappa$, where all the levels have size $<\kappa$ has a branch of length $\kappa$. This is the generalized Koenig's lemma. So we can prove $\omega$ has the tree property and $\omega_1$ doesn't; and we can prove that singular cardinals don't have it either. But what about the rest? It is consistent relative to a weakly compact cardinal that $\aleph_2$ has the tree property, or any other fixed successor of regular cardinal, other than $\aleph_1$. [...] – Asaf Karagila Jan 26 '15 at 12:31
-
1[...] It was shown, however, that the consistency strength for two successive (or more, of course) cardinals with the tree property is much higher than that of a weakly compact cardinal. The successors of singular cardinals are also very difficult to deal with, and so to get the tree property at a successor of singular (e.g. $\aleph_{\omega+1}$) we need much larger large cardinals. And we can show that if there are $\omega$ supercompact cardinals (very large large cardinals), then we can arrange a model where they become the new $\aleph_n$'s and $\aleph_{\omega+1}$ has the tree property. – Asaf Karagila Jan 26 '15 at 12:34
-
4It is unfortunate that this question is now attracting delete votes. – Jun 14 '19 at 17:46
-
1Although I believe this type of question will likely be closed, & possibly deleted, fairly quickly now, I don't think this question should be deleted. I wasn't a member then, but I assume the general site criteria for acceptable questions was somewhat different then, over $4$ years ago. I believe it's best to limit to what extent we impose the current standards on these historical questions. Also, note this question has attracted quite a few answers, at least several that I've looked at now which I consider to be quite good, plus a lot of views, so it seems to have a lot of interest. – John Omielan Jun 15 '19 at 01:26
39 Answers
I really like the proof of $$\sum_{i=1}^n i = \dfrac{n(n+1)}{2}$$ in which $1 + 2 + \cdots + (n-1) + n$ is written forwards then backwards and summed. It is claimed that Gauss had come up with this when he was just a child, although contested.
The proof
Let $$s = 1 + 2 + \cdots + (n-1) + n.$$ Clearly, $$ s = n + (n-1) + \cdots + 2 + 1.$$
Sum to get $$2s = \underbrace{(n+1) + (n+1) + \cdots + (n+1) + (n+1)}_{n \text{ times}}.$$
Hence, $$2s = n(n+1),$$ and $$s = \dfrac{n(n+1)}{2}.$$
- 6,478
-
4
-
1
-
1Here says $8$ years old. But I never trust a single source alone, so I'll look around a bit a more. – Ivo Terek Jan 17 '15 at 23:30
-
-
1@GabrielH http://hsm.stackexchange.com/questions/384/did-gauss-find-the-formula-for-123-ldotsn-2n-1n-in-elementary-school – Jack M Jan 17 '15 at 23:32
-
1Here also says $8$ years old. Here says $7$. I think it is safe leaving at $8$ for now :) – Ivo Terek Jan 17 '15 at 23:33
-
4Edited to say "when he was just a child", this should cover most claims :) – MathMajor Jan 17 '15 at 23:34
-
2
-
4As a motivation note that this formula can also be used to calculate the number of clinks of glasses in a group of n+1 people. – Roman Reiner Jan 18 '15 at 01:23
-
18@GabrielH It was known long before Gauss. And the story about Gauss is possibly apocryphal. – Thomas Andrews Jan 19 '15 at 04:26
-
1
-
7For what? Fermat was proving theorems about triangular numbers a century before Gauss was born. As for the story about Gauss being apocryphal, the real question is, what source do you have to support it? Bell's book contains a lot of bunk, and it is a source of a lot of random myths about mathematicians. @GabrielH – Thomas Andrews Jan 19 '15 at 04:51
-
2See the Wikipedia page for Gauss as to whether the story is actually true: "However, the details of the story are at best uncertain (see[40] for discussion of the original Wolfgang Sartorius von Waltershausen source and the changes in other versions); some authors, such as Joseph Rotman in his book A first course in Abstract Algebra, question whether it ever happened." Basically, it has no foundation. @GabrielH – Thomas Andrews Jan 19 '15 at 04:53
-
2As for prior knowledge for triangular numbers, even Dickson's "History of the Theory of Numbers" ignores that case, but it does say at one point: "(1676) Leibniz concluded, from the expressions for the $y$th triangular and pyramidal numbers, that..." So that's a hundred years before Gauss was born. – Thomas Andrews Jan 19 '15 at 05:29
-
1@ThomasAndrews That late? It's hard to believe that Archimedes, Euclid, and Pythagoras didn't know the formula for triangular numbers, or the sum of an arithmetic progression. – bof Jan 19 '15 at 08:10
-
3My goal was only to find a reference before Gauss. As I said, I couldn't find any historical information. I suspect the Pythagoreans knew the formula. @bof – Thomas Andrews Jan 19 '15 at 08:12
-
No one should claim that Gauss deserves credit for the formula, but he may have rediscovered it at a very young age. The Brian Hayes article cited in the Wikipedia quote is well worth reading. Some highlights: the earliest known source for the story is a tribute to Gauss written a year after his death, and the story is attributed to Gauss himself. This version does not say what numbers were to be summed, or what Gauss's method was; these may be later elaborations. To say the story has "no foundation" is too strong. – Will Orrick Jan 19 '15 at 16:18
-
@ThomasAndrews Okay, I changed the wording so it doesn't sound anything close to a "known fact", rather a suggestion. – MathMajor Jan 20 '15 at 00:30
-
4@ThomasAndrews I doubt little Gauss had read any of Fermat's work. It's a very real possibility that he found it independently as a kid, I don't see why he couldn't. Maybe didn't discover it to the world but there's no need to discredit the story. – Shahar Jan 20 '15 at 02:10
-
3@Shahar Please read what I wrote. I made two statements: This formula was known before Gauss, and some people think the Gauss story is apocryphal. I was asked for citations, without specifying which claim needed citations, so I provided citations for both. I know a young man can figure out the trick, because I did it at nine years old (although I was given the hint that there was a trick.) – Thomas Andrews Jan 20 '15 at 02:15
-
@GabrielH: Did you look at Brian Hayes' article? The Gauss story is as close to a "known fact" as many biographical items ever get. Quite a few authors have added their own elaborations, but the basic outline goes back to the era when Gauss lived, and is a story recounted by Gauss himself. I have not seen any argument for doubting it. – Will Orrick Jan 20 '15 at 06:28
-
@WillOrrick There is so much speculation on this in the comments that I will just leave the note that it is contested, which does not mean I am asserting it is false. People can look at the comments and decide for them selves. – MathMajor Jan 20 '15 at 06:41
-
@WillOrrick " the basic outline goes back to the era when Gauss lived, and is a story recounted by Gauss himself." Source, please. – guest Jan 20 '15 at 07:10
-
@guest: have you read the rest of the comment thread? Is there something you object to in the source already given? – Will Orrick Jan 20 '15 at 13:32
-
@WillOrrick From the previous comment: " Some highlights: the earliest known source for the story is a tribute to Gauss written a year after his death, and the story is attributed to Gauss himself." From the comment above: "... is a story recounted by Gauss himself." Attributed to Gauss, and provably recounted by Gauss is not the same thing. – guest Jan 21 '15 at 03:51
-
@guest: The story, as far as we know, doesn't appear in Gauss's own writings, if that's what you're driving at. We only have the word of one of Gauss's Göttingen colleagues that it was "an incident which he often related in old age with amusement and relish." – Will Orrick Jan 21 '15 at 04:35
-
@IvoTerek: "Here says 8 years old. But I never trust a single source alone, so I'll look around a bit a more." The original source of the story appears to be Gauss zum Gedächtnis, which suggests that Gauss was nine years old when the incident occurred. He started at the Katherinenschule in 1784, at age 7, and entered the arithmetic class two years later, which is where the account says the event took place. By age 10, we find Gauss and the teacher Büttner's assistant, Martin Bartels, engaged in self-study ... – Will Orrick Jan 25 '15 at 04:47
-
... in mathematics, Gauss having surpassed what the school could teach him. In 1788, Gauss started at the Gymnasium. Bartels also became a mathematician, and he and Gauss remained friends. (There is an English translation of the source by Gauss's great-granddaughter, but see Brian Hayes' article for some comments about interpolations made by the translator.) – Will Orrick Jan 25 '15 at 04:48
-
2This is so trivial that I figured it out myself as a kid... I am pretty sure that Gauss 7 or 8 would have no problem rediscovering this. – bjedrzejewski Jan 26 '15 at 13:25
-
2I just wanted to mention that I, too, discovered a similar formula as a child (if middle school counts), and I'm certainly no Gauss! What I discovered was a little different: Sum of a fixed-step sequence = the median multiplied by the count of numbers. For example sum of (1, 2, 3, 4) = 2.5 x 4 = 10. Sum of (2, 4, 6, 8, 10) = 6 x 5 = 30. Sum from 1 to 100 = 50.5 x 100 = 5050. – MyNameIsKhan Jan 26 '15 at 14:32
-
3The story that I read (many years ago) was that a school teacher gave the kids the task to add the numbers from 1 to 1,000 to shut them up for a while. And six year old Gauss added (1 + 1000) + (2 + 999) + ... + (501 + 500), which means 500 sums each equal to 1001 = 500,500. No need for a general formula, which makes it a lot easier. At age nine, I would be impressed if my grand children could figure it out themselves, but I wouldn't be impressed with a nine year old Gauss. – gnasher729 Jan 26 '15 at 14:45
I'm a bit reluctant to throw another answer on the pile, especially because I think there are other lists on this website which serve a pretty similar purpose. However, I think an excellent 5 minute blurb could be given to a general audience on the trick, attributed to von Neumann, for performing a fair coin toss when only a biased coin with unknown bias is available. There is a wikipedia entry on this. Here is an informal description:
Suppose you have a biased coin. The chance that the coin comes up heads or tails (assume both are actually possible) are unknown to you, but do not change from toss to toss. You and your friend Jane wish to use this coin to decide (fairly) which of you gets the top bunk at math camp.
Jane makes the following observation. Suppose the coin is flipped twice in a row. The possible outcomes are: \begin{align*} HH && TT && HT && TH \end{align*} Now, we do not know how likely each of these outcomes is, but one thing is certain: $$ \text{ The outcomes $HT$ and $TH$ are equally likely.}$$ Because of this observation, you agree on the following fair way to settle the dispute. You "call" the outcome $HT$ while Jane "calls" the outcome $TH$, and then proceed to flip the coin twice. If either $HH$ or $TT$ occurs, a mistrial is declared and you start over, flipping the coin another two times. Eventually, either $HT$ or $TH$ will occur, and the dispute is settled.
I think this works well because:
- It is simple -- simple enough to fit into 5 minutes.
- It requires no special knowledge from the audience. People generally have pretty reasonable built-in intuition for probability.
- It is a beautiful, but also practical, idea -- making it effective as "Math P.R."
- You can also actually demonstrate the procedure, to make sure it is understood, without any special equipment. Just take something such as a thimble which can land either of two states, but for which it is not clear that either outcome is equally likely.
-
2Excellent suggestion! This is a very simple and very creative solution to a problem that is very easily stated. Thank you! – userX Jan 19 '15 at 06:46
-
2Small comment: we are assuming that the coin's bias does not affect the independence of each coin flip (i.e. each coin flip is independent of the others). – Ryan Dougherty Jan 19 '15 at 15:57
-
57I upvoted this terrific answer, but the statement "People generally have pretty reasonable built-in intuition for probability" is probably the most demonstrably false statement on this entire SE spinoff. – dotancohen Jan 20 '15 at 06:44
-
-
@Ryan: Although I didn't write that the trials were independent, I did write that the chances the coin shows heads/tails "do not change from toss to toss". It seems to me this implies independence. – Mike F Jan 21 '15 at 05:17
-
1Could you also just pick a side (heads or tails), and toss it, since you don't know the probabilities of each side, so the chance of you choosing either side is 50/50? – rlms Jan 21 '15 at 19:05
-
@sweeneyrod: That's an interesting comment. Even still, for many "coins" it may be clear that, for instance, "heads" is more likely than "tails", but not clear how significant the bias is. For instance, a thimble is more likely to land on its side than its end. – Mike F Jan 21 '15 at 21:27
-
You don't have to discard the mistrials! What the coin gives you goes into level 0. If you get HH in any level, delete it but add a H to the next level. This way in fact extracts the maximum amount of information from the random stream. – user21820 Jan 22 '15 at 11:47
-
2@sweeneyrod: No the chance of you choosing either side is not 50% simply because you chose it. Whether you knew the probabilities does not make a difference because for your method to work you have to assume that you randomly choose between two choices perfectly unbiasedly! – user21820 Jan 22 '15 at 11:51
-
@user21820: Discarding the mistrials is definitely important. Here's what can happen if you don't: Assume $H$ is much more likely than $T$. I claim, then, that $HT$ is much more likely than $TH$. Indeed, the sequence of flips will very likely look like $HHHHHH \ldots HHHT$ so the first distinct pair to occur in sequence is $HT$. – Mike F Jan 22 '15 at 16:59
-
You didn't read what I said carefully. When you get a double in a level you delete it; you don't leave any behind! So if you divide your sequence into pairs you will find that the first pair with different outcomes is equally likely to be "HT" or "TH", regardless of the bias of the coin. The rest will have gone into the next level. As I said, the method I described gives an unbiased binary stream with maximum entropy. – user21820 Jan 23 '15 at 05:53
-
4@sweeneyrod If you don't know whether the coin's biased towards H or T, then it's Mathematically valid to call H or T and toss the coin once. However, this requires John to trust your claim that you don't know. This is unacceptable in many situations where coin tosses are used; eg. if John loses the toss, he may feel like you cheated. By using HT/TH combinations, you can both verify that it's fair, without any need for trust. – Warbo Jan 24 '15 at 17:16
-
Another reason I like it - the more biased the coin is, the longer it takes to get one random bit out – zodiac Feb 20 '15 at 05:19
The harmonic series diverges because otherwise there exists a finite number \begin{align*} S &= 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\dotsb \\ &= \left(1+\frac{1}{2}\right)+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}\right)+\dotsb \\ &> \left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{6}+\frac{1}{6}\right)+\dotsb \\ &= 1+\frac{1}{2}+\frac{1}{3}+\dotsb \\ &= S \end{align*}
- 26,559
I'd probably go for Euclid's beautiful proof of the infinitude of primes, as it doesn't require much knowledge beyond elementary school.
Edit: Another possibility might be the pictorial proof that the derivative of $x^2$ is $2x$ by a square whose side length, $x$, increases and what that means to the rate of change of the area
- 1,027
-
my top choice as well; aside from the main argument (which is short) all you really need to show is that consecutive integers are coprime, which itself is an easily-proved yet intuitive fact. – Coffee_Table Jan 18 '15 at 00:03
-
36Yes! But never forget to state what happens if $p_1p_2...p_n+1$ isn't prime, or the audience ends up thinking it's always prime (like it happened to me). – user2103480 Jan 18 '15 at 00:11
-
-
6@Amjad If $p_1p_2\cdots p_n$ are all the primes, then $p_1p_2\cdots p_n+1$ is prime. And it is not prime. And it is zero. That is the nature of a proof by contradiction. :) – Thomas Andrews Jan 19 '15 at 14:29
-
10@ThomasAndrews I think Amjad is referring to the fact that the proof buys you more than the infinitude of primes. If $p_1,p_2,...,p_n$ are the first $n$ primes, then all of the prime factors of $N=p_1p_2...p_n+1$ are larger than $p_n$. So you can always produce a larger prime using this method, but you might have to factor $N$ to find it. – Steven Gubkin Jan 19 '15 at 19:44
-
@Amjad: Regarding the derivative of the area of a square. Do you mean that the derivative shows a relationship between area and perimeter? i.e., if we measure $x$ to be the length from the center of a square to an edge, then the area of the square is $4x^2$ and the derivative is the square's perimeter ($8x$). If you could provide more information on this second point in your post, that would be great. – rookie Jan 21 '15 at 16:42
-
2The derivative shows a relationship between area and sidelength - you draw a square with sidelengths "x" and then extend it by "h". For an "input" of a small h to the sidelength you get an "output" of 2xh + h^2 in terms of area. As the derivative measures, in loose terms, output over input, you get a rate of change of 2x + h for the area, with h getting neglectably small. Nothing too special about this rather informal proof, but I kinda like it. – user2103480 Jan 21 '15 at 18:27
-
@ThomasAndrews $p_1p_2...p_n+1$ is only prime if your set of primes is all the primes up to $p_n$. If you assume your $p_i$ are just a finite set of primes, the proof still works but $p_1p_2...p_n+1$ may not be prime. The only thing you know is that it isn't a multiple of any p in your original set. – Holloway Jan 23 '15 at 16:53
-
1I was just being irritatingly pedantic - if you do the proof as "by contradiction," then we are assume $p_1,\dots,p_n$ are all the primes, and the contradiction thus allows you deduce anything, including that $p_1p_2\dots p_n+1$ is prime or even that $1=2$. @Trengot – Thomas Andrews Jan 23 '15 at 17:46
Existence of Eulerian walks and the whole 'seven bridges of Königsberg' story. It's a cliché, but it's not about numbers (which is a plus when talking to a general audience), and it's something people can find at least mildly amusing. The argument is simple and everyone can follow it, and the best thing is, it's not just a clever solution to what looks like a random puzzle, which I feel is the impression people can get when shown other simple proofs. Starting from the seven bridges perspective and replacing shores and islands with vertices and bridges with lines, this proof is the best toy example I know of of the power of mathematical abstraction.
- 3,962
-
4i have to agree this is one of the best examples fitting all the criteria for general audience etc.. thank you! – userX Jan 18 '15 at 01:48
-
13The vast majority of the general audience seem to think that "mathematics is about numbers". I like this example because it has almost nothing to do with numbers; it demonstrates that maths is far more than just opaque equations and stuff. – MathematicalOrchid Jan 19 '15 at 09:54
-
1@MathematicalOrchid: Mathematics had mostly not been about opaque equations and stuff until recently... – user21820 Mar 21 '15 at 05:44
There exist irrational $x$ and $y$ such that $x^y$ is rational.
proof: if $\sqrt{2}^\sqrt{2}$ is rational we're done, otherwise we consider $(\sqrt{2}^\sqrt{2})^\sqrt{2}$, which evaluates to $2$.
edit: simpler to fit any audience, but somewhat related, the proof without words of the irrationality of $\sqrt{2}$
later edit: also Euclid's proof of the infinity of the primes is a good candidate
- 537
- 12,285
-
33Keep in mind the definition of "general audience". Will a general audience understand exponent rules with irrational exponents? Will they even appreciate what an "irrational number" is? – Jack M Jan 17 '15 at 23:34
-
4
-
@JackM they might not appreciate the beauty, but I think a person with a bachelor, as is the average guy defined in the question would be able to follow – Alessandro Codenotti Jan 17 '15 at 23:41
-
-
8@1110101001: that expression evaluates to $2$ so I'm pretty sure it isn't irrational – Alessandro Codenotti Jan 18 '15 at 01:16
-
4
-
2I don't see how's better, it's perfectly equivalent, but the $\log$ is even more confusing for the general audience. Also I'm sure i can show to the average audience that $\sqrt{2}$ is irrational, is there such a simple proof also for $\log_29$? – Alessandro Codenotti Jan 18 '15 at 23:53
-
1The problem with this proof is that someone in the audience might know that $e$ and $\ln (2)$ are irrational. And then the proof suddenly looks more complicated than it needs. – N. S. Jan 19 '15 at 02:13
-
5@Alessandro It is better because it is constructive. To show that $\log_2{9}$ is irrational suppose it were equal to $m/n$. Then $2^m = 9^n$ which is impossible since $2$ does not divide the right hand side. – Jan 20 '15 at 14:36
The fact that $$1 = \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ ...$$ by drawing the following picture of a square with a side length of $1$:
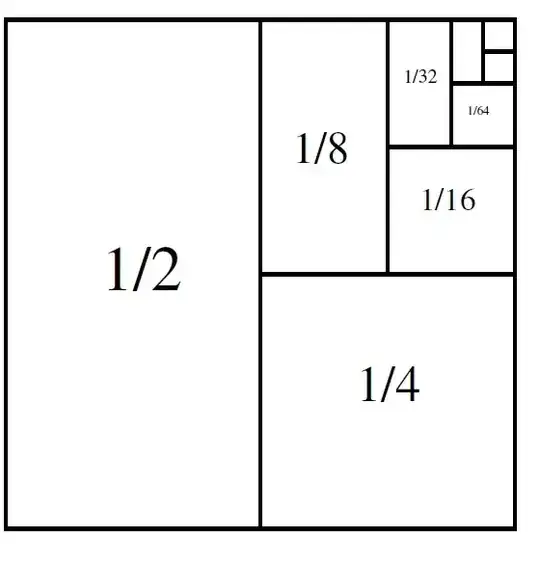
- 971
-
There's a nice proof in there that $\sum_{n\geq1}2^{1-2n}=\frac23$ if you shade the rectangles too. – it's a hire car baby Jun 15 '19 at 12:24
If you would say ten minutes, I'd go with $\sqrt2$ is irrational. Because that's a bit time consuming, since it can be a bit confusing for people less familiar with these things.
Instead, let's prove that $2+2$ is $4$.
Begin with axioms, mathematical proofs begin with axioms:
- $0$ is a natural number, and $1$ is the successor of $0$.
- For every natural number $n$, there is a successor $n+1$.
- For every natural number $n$, $n+0=n$ and $n+(k+1)=(n+k)+1$.
- $2=1+1$, $3=2+1$, $4=3+1$.
Theorem. $2+2=4$.
Proof. $2+2=2+(1+1)=(2+1)+1=3+1=4$.
The proof is important, since this shows both that proofs begin with axioms, and that we have to prove things which may seem obvious to us. But also, it will reassure them that $2+2=4$.
- 393,674
-
I like this suggestion (far better than the $\sqrt{2}$ option) a lot. Are you sure a 'general audience' will be able to actually understand the amount of bracketing going on here? – HSN Jan 17 '15 at 23:40
-
You can always omit the parentheses, and write $ssss0$, and only add parenthesis when it's needed (e.g. $s(2+s0)$ and such cases). – Asaf Karagila Jan 17 '15 at 23:41
-
-
3You know what, you can even go for broke, and write $n+1$ for the successor. – Asaf Karagila Jan 17 '15 at 23:43
-
@Asaf thank you I think this example is excellent. I really like that all the needed axioms are stated and used. This has key mathematical ingredients and is extremely accessible. I also like the way you had it before with the $s$ but this is nice, thank you ! – userX Jan 18 '15 at 07:12
-
1@userX: I prefer, to some extent, the $s$ notation, since it separates the addition of $+$ from the successor operator; but for sufficiently non-mathematical crowd, I'd opt for the $+$ notation to make it easier to understand. – Asaf Karagila Jan 18 '15 at 07:14
-
-
27I like the 2+2=4 but I am wondering if it would not strenghten the prejudice that mathematicians are pettifoggers. Have you ever shown that proof to a general audience? I would be interested in hearing about the audience's reaction. – Taladris Jan 18 '15 at 22:48
-
1@Taladris: I never had to speak to an audience of that nature. I did explain various difficult proofs (compared to this one) to people, and saw them nod in semi-understanding while I was doing that. The problem with mathematics is that the beautiful parts are rarely accessible to a general audience. Not only that, they are rarely accessible to a general audience of mathematicians. – Asaf Karagila Jan 18 '15 at 22:53
-
92I do not think that a "proof of 2 + 2 = 4" will leave any positive impression about mathematics on an average educated person. – Jan 18 '15 at 23:20
-
10@Taladris As a teacher, this is precisely the point I am most interested in. If we assume that, "the beauty of math is not accessible to the general public", a corollary of that may be "math can only be enjoyed by some elite club of gifted thinkers". I don't believe this to be true, since none of us were born into this elite club. We all entered somehow into this set of people who enjoy and see beauty in math. I think statements such as ones found on this page are catalyst to open the doors wide so that more people belong to this set (see http://youtu.be/Yexc19j3TjE ) – userX Jan 19 '15 at 01:57
-
2A somewhat similar experience: during a lesson on rational exponents in high school, my colleague show that if $\frac{a}{b}=\frac{c}{d}$, we have $x^\frac{a}{b}=x^\frac{c}{d}$ for any $x>0$. He really enjoy this proof; students (that I think to be not far from the "general audience") don't see the point. PS: I am not a downvoter. – Taladris Jan 19 '15 at 10:14
-
1@Taladris: I wouldn't have seen the point in proving that theorem either; $2+2=4$, however is (1) iconic Orwellian reference; and (2) much simpler. The importance is that it shows that mathematics require proof. $2+2=4$? How do you know? Of, you count on your fingers, what if the next time you somehow count $3$ or $5$ or $216$? Experimentation is evidence, not proof. – Asaf Karagila Jan 19 '15 at 15:07
-
Of course the beauty here is that axiom 4 saved us from defining summation. – kutschkem Jan 21 '15 at 13:39
-
@kutschkem: Well, we still have to define the meaning of the symbols $2,3,4$ and so on. – Asaf Karagila Jan 21 '15 at 18:26
-
1Most people would be disappointed to see a proof of something "obvious" derived from statements that would appear arbitrary and maybe even more complicated than the final "theorem" to them. I think to justify all this you will need more than 5 minutes (it is a worthwhile thing, just not likely to be done quickly). Moreover overloading the notation for + will most likely entirely lose the audience. – Sasho Nikolov Jan 24 '15 at 02:43
-
@Sasho: My original suggestion was to present the proof that from $\omega$ supercompact cardinals we can have the tree property in all the $\aleph_n$ (for $n>1$ anyway). But the point is that anything you can present as a proof in five minutes will either bore the audience or go over their head. I also disagree about overloading the $+$, but the original version of the answer had a separate operator for the successor. – Asaf Karagila Jan 24 '15 at 10:23
-
1I disagree: there are answers to this question which can be presented in 5 minutes and will not be boring (infinitude of primes). In any case my concern with your example is not that it's a complicated proof (it certainly is not). But people have very stable notions of the naturals and understanding the need for a rigorous construction would be a significant conceptual shift and may actually be a bigger challenge to convey than a more complicated argument. But as I said it's worthwhile and maybe I am underestimating people. – Sasho Nikolov Jan 24 '15 at 17:50
-
1@Sasho: I agree that the infinitude of primes is a better example (and by the time I had thought about it, there was an answer suggesting that already). But I also think that "it's obvious there are infinitely many primes". Maybe less obvious than $2+2=4$, but it's still somewhat obvious if you think about it for a moment, even if you don't really see how to prove it. Giving a nearly trivial proof, and showing how proving someone from definitions works, is a much more accurate depiction of mathematics in my opinion. With the five minutes one can motivate the axioms and proof nicely, I think. – Asaf Karagila Jan 24 '15 at 17:53
-
1@Sasho: In any case, I am not quite interested in starting a discussion here over the merits of this example. I think it's a good example, and I think that one of the most difficult questions I had as an undergrad was to prove that $0+x=x$ from the field axioms, which said that $x+0=x$ (I had to apply commutativity and the said axiom). Simply because it was so obvious. It's a good thing if we explain to people that mathematicians have basic axioms and definitions and they derive things from there, and not from thin air. But in any case, I am not looking for a discussion here. Have a nice day! – Asaf Karagila Jan 24 '15 at 17:55
The Mutilated chessboard problem:

Suppose a standard 8x8 chessboard has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2x1 so as to cover all of these squares?
has an easy parity-based solution:
The puzzle is impossible to complete. A domino placed on the chessboard will always cover one white square and one black square. Therefore a collection of dominoes placed on the board will cover an equal numbers of squares of each colour. If the two white corners are removed from the board then 30 white squares and 32 black squares remain to be covered by dominoes, so this is impossible. If the two black corners are removed instead, then 32 white squares and 30 black squares remain, so it is again impossible.
- 41,546
- 4
- 46
- 89
-
The picture is inconsistent - On the checkerboard the Black corners are missing, but there is a picture of two white squares and you talk about missing white corners ? – Falco Jan 20 '15 at 09:57
-
1@Falco, the 2x1 piece is simply a domino and the proof is good in both cases. – Martín-Blas Pérez Pinilla Jan 20 '15 at 11:00
I am reading some great responses, thank you all, keep them coming please, I love these. I'd also contribute with another of my favorite ones. Not so much a proof but a 'reasonable argument" for the area of a circle. Most 'general audience' members know $$a=\pi r^2$$ but I am often surprised at how few of them have ever seen a proof for this, similarly but not to same extent for Pythagorean theorem, everyone has seen/used these theorems but few have every seen a proof or even a sketch of a proof,
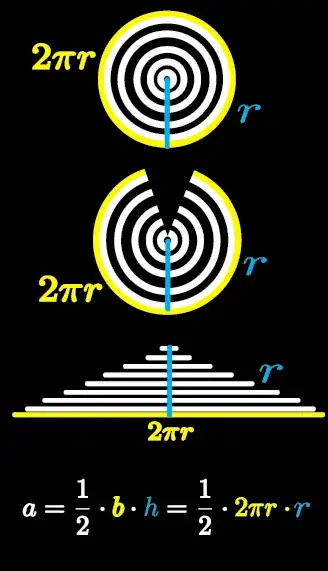
- 2,029
-
1I haven't done a formal proof in a while, but I think it is easier to derive the area of the circle from first principles than to derive the circumference of the circle from first principles. Am I mistaken? – Ian Jan 18 '15 at 05:47
-
5@Ian: π is usually defined in terms of half the circumference of the unit circle, in which case there is nothing much to prove to derive the circumference of an arbitrary circle. The difficult part if mathematical rigour is desired is actually in defining circumference and area themselves... – user21820 Jan 18 '15 at 06:01
-
@lan I'd be interested in seen such a proof .. I've never seen an elementary proof that does not use the circumference result. – userX Jan 18 '15 at 06:47
-
11@userX Seeing that you really get a triangle when you "unroll" the circle is nontrivial. – Zubin Mukerjee Jan 19 '15 at 04:30
-
24This picture annoys me because it stops one step too early. There should be one more step that takes the right-hand half of the triangle, turns it upside down and places it atop the left-hand half of the triangle to obtain an $r\times \pi r$ rectangle, eliminating the need to invoke $A=\frac12bh$. – MJD Jan 19 '15 at 04:50
-
6
-
@MJD I didn't think about it before but yes, I concur. That would make it much cleaner. – userX Jan 19 '15 at 06:10
-
18"Reasonable arguments" in pictorial format aren't always reasonable. – 200_success Jan 19 '15 at 12:59
-
1"Not so much a proof but a 'reasonable argument' for the area of a circle." Is there a difference when talking to the general public? Of course, you as a mathematician need to know that things makes sense behind the scenes, but the general audience probbably cannot tell the difference. – Arthur Feb 09 '15 at 09:30
-
@Arthur The general public not being able to tell the difference is not a reason to delude them :) – anderstood Feb 18 '15 at 15:08
Plenty of people are dumbfounded when you suggest to them that $0.\overline{999}$ might be equal to $1$. Regardless of whether or not the following is rigorous, I've found it to be a wonderful way of demonstrating the property that only requires an understanding of simple algebra.
\begin{align} \textbf{let } x &= 0.\overline{999}\\ 10 \cdot x &= 10 \cdot 0.\overline{999}\\ 10x &= 9.\overline{999}\\ 10x - x &= 9.\overline{999} - x = 9.\overline{999} - 0.\overline{999}\\ 9x &= 9\\ x &= 1\\ 0.\overline{999} &= 1 \end{align}
- 319
-
1Great example! If I may suggest a change, I think substituting the forth line by $10x=9+0.\overline{999}=9+x$ is clearer (no "infinite substraction" involved). – Taladris Jan 18 '15 at 22:52
-
34I don't like these proofs at all, since it always looks like mathematical trickery, if you add/multiply over several lines, because there are also some fake proofs for 1=0 with the same process. - I prefer this proof: What is 1/3 ? 0.333... ok and what is 0.3333 times 3 ? 0.99999 -> 1/3 times 3 is one. So it's the same. – Falco Jan 19 '15 at 09:47
-
11@Falco I think that argument is less valid. If somebody believes $0.\overline{999}<1$, why not also believe that $0.\overline{333}<\frac{1}{3}$? – Peter Olson Jan 20 '15 at 03:18
-
5@PeterOlson Then I would ask them:
Ok, please write 1/3 for me in decimal notation... exactly 1/3 not more or less.And if they accept you cannot write 1/3 exactly with a finite number of decimals, they will truly understand why we need periodical numbers - double win ;-) – Falco Jan 20 '15 at 09:38 -
6@Falco What if they accept that you can't write 1/3 exactly with a finite number of digits, but also say you can't do it with an infinite number of digits either? Your request doesn't seem that different from
Please write 1 for me in decimal notation starting with 0 followed by a decimal point. Exactly 1, not more or less.to which the response would likely be that you can't do that, with either a finite or infinite number of decimals. – Peter Olson Jan 20 '15 at 14:34 -
@PeterOlson If someone is so much bound on denying periodical numbers, I doubt that some fancy number changing will help him. He could as well say "you cannot subtract in the 4th line, because one 9 is missing at the end and will still be left, so it isn't exactly 9, but 8,999....9991" - But maybe there are some people who prefer the formula over my 1/3 approach, who knows – Falco Jan 20 '15 at 15:29
-
3We could debate endlessly what the "average person's" mathematical intuition is I suppose. But personally, I don't think it's any more obvious that 1/3=.333... than that 1=.999... But saying that .999... x 10 = 9.999..., I think most people would accept. You've said it's an infinite number of 9s, so "pushing" one in front of the decimal doesn't take away any at the end. – Jay Jan 21 '15 at 14:40
-
1An even better question is, "what rules of long divison are needed to get the answer 0.9999.., when previously we would have given 1.0?" ;-) – Philip Oakley Jan 21 '15 at 14:41
-
1Any explanation for $0.999...=1$ that doesn't start with the definition of an infinite series is worthless - worse than that, it's misleading about the nature of mathematics. The fundamental thing to understand about $0.999...=1$ is that it is true by definition, it's not fundamentally true in some cosmic, platonic sense. It is simply that the notation $0.999...$ makes no sense without a definition, and the definition which we happen to use leads to its value being $1$. – Jack M Jan 23 '15 at 21:24
-
I agree with @Falco, and was going to write the same comment. People get that 0.333 recurring is 1/3, but that 0.999 recurring is 1 is still pretty mindblowing. – Rob Grant Jan 26 '15 at 08:54
-
My favorite proof of the fact that $0.\overline9=1$: "If they were different, there'd be something in between them." – Akiva Weinberger Mar 30 '15 at 01:55
-
My favourite proof of this is to simply ask somebody to write the number they would have to add to $0.\overline9$ in order to make it equal $1$. They realise there is no solution but $0.\overline0$ – it's a hire car baby Jun 15 '19 at 12:29
I'm fond of the proof of Fermat's little theorem by 'counting necklaces'. It is a nice application of combinatorics that most people can follow. You start by stating the theorem as $p \mid a^p - a$ to avoid explaining congruences. It goes like this:
Take an alphabet with $a$ letters, and form all possible strings $S$ of length $p$. There are $a^p$ of them. We remove all the strings consisisting of a single character, and look at the remaining $a^p-a$ strings. We want to split them into groups of size $p$. Consider the strings as necklaces: connect the first and last letter. Imagine that two necklaces are 'friends' if you can obtain one from the other by sliding letters around, so for example the string $ABABA$ would be friends with $BABAA$. We claim that if a string $S$ cannot be broken into several copies of a shorter string $T$, so $S \neq TT\dots$ for some $T$, then $S$ has exactly $|S|$ friends. This is easy to argue informally, because it can't have more, and if it had fewer, then it would repeat itself. But $p$ is a prime, so the strings can't possibly be broken down to pieces. Hence every group of friends has exactly $p$ members. (If $\varepsilon$ is big, and you have the time, you can argue that being friends in this case is an equivalence relation). Since every friend group has $p$ members, we have divided $a^p - a$ strings into $p$ groups, so $p \mid a^p-a$.
- 60,406
- 6,118
-
I remember enjoying proofs of this based on group theory or combinatorics.. I don't remember a 'counting necklaces' proof but I will look that up. Thank you – userX Jan 18 '15 at 02:06
-
-
2I see it, very nice! I can see why you like it, it is a very clever argument, and no group theory whatsoever, pure combinatorics and almost no combinatorics, amazing. thank you for sharing this. – userX Jan 18 '15 at 02:39
-
-
4A good way to spice this proof up* is to change necklaces to pizzas and beads to pizza toppings. (*pun not intended, but then reconsidered and intended after all.) – Yoni Rozenshein Jan 19 '15 at 00:31
Insolvability of the $15$-puzzle.
Not directly accessible to everyone but I found that with a lot of effort most people will eventually understand it.

(Picture from Wikimedia commons.)
Theorem. Slide the blocks until 14 and 15 have swapped positions and all other blocks have returned to their initial positions. You won't succeed: it's impossible.
Sketch of Proof. The required number of moves is odd, because it corresponds to the permutation (14 15). (The general audience may learn this fact by drawing pictures that illustrate that the parity of the number of orbits changes with every move, or because they learned to comute determinants at some points in their lives.) On the other hand, the required number of moves is even because at each step the 'hole' moves from a black to a white square when colored as a chessboard, so since the hole returns to its original position it is impossible to swap 14 and 15.
- 8,781
-
3There is a nice proof where you don't need to talk about permutations. Notice that when you move left or right then the number of disorders (a disorder is a pair of pieces with numbers such that $x<y$ and $y$ is before $y$ while going line by line horizontally) do not change but when you move up or down then number of disorders change by an odd number and number of the row where the empty place is changes by one (again odd number). The starting position has even number of disorders and empty piece in row number 1. If you swap 1 and 2 you have 1 disorder and empty piece in row 1. Contradiction. – pw1822 Jan 18 '15 at 23:06
-
I love these puzzles, and can solve them quite quickly (although I guess it's not hard once you know how), and this little problem is one of my favorites. – A. Thomas Yerger Jan 19 '15 at 04:21
-
It wasn't clear to me at first that "Slide the blocks until 14 and 15 have swapped positions" meant that all the other numbers must be returned to their starting locations. I only guessed that was a requirement since without it, it's easy to swap 14 and 15. – Todd Wilcox Jan 20 '15 at 14:12
-
1@ToddWilcox Good point I've noticed before that this tends to confuse people. I have added it, hope it's clear now! – Myself Jan 20 '15 at 14:14
Problem: An old car has to travel a 2-mile route, uphill and down. Because it is so old, the car can climb the first mile, the ascent, no faster than an average speed of 15 mi/hr. How fast does the car have to travel the second mile, on the descent it can go faster, of course, in order to achieve an average speed of 30 mi/hr for the trip?
Solution/Proof: It's impossible! Let $r$ be the rate of descent. We use the formula $$ \mathrm{time} = \frac{\mathrm{distance}}{\mathrm{rate}}; $$ the ascent takes $\frac{1}{15}$hr, the descent takes $\frac{1}{r}$hr, and the total trip should take $\frac{2}{30}=\frac{1}{15}$hr. Thus we have $$ \frac{1}{15}+\frac{1}{r}=\frac{1}{15}\Longleftrightarrow \frac{1}{r}=0, $$ which is impossible. So the car cannot go fast enough to average 30 mi/hr for the 2 mile trip.
Historical note: This question was actually sent to Albert Einstein by his friend Wertheimer. Einstein, and his friend Bucky, enjoyed the problem and had the following to say in a response letter to Wertheimer:
Your letter gave us a lot of amusement. The intelligence test fooled us both (Bucky and me). Only on working it out did I notice that no time is available for the downhill run!
More detail about this exchange between Einstein and Wertheimer may be found here.
I think this problem is excellent for a general audience because the problem statement is crystal clear, and the knee-jerk reaction (i.e., 45 mi/hr) is completely off-base. It also does not take too much time to explain that the uphill journey takes $\frac{1}{15}$hr while, in order to average 30 mi/hr for a 2 mile trip, the total trip must take a total of $\frac{2}{30}=\frac{1}{15}$hr. Thus, uh oh! No time for the downhill run.
- 22,531
-
1Very nice and surprising! I enjoyed this very much and I think the historical anecdote adds to the appeal – userX Jan 18 '15 at 18:18
-
21Here's another way to think about this without getting into calculations. Imagine a phantom car that leaves at the same time and travels at the desired speed of 30 mi/hr. We need to arrive at the finish line at the same time as the phantom car—but after the first mile, the phantom car has just arrived at the end. – Théophile Jan 19 '15 at 05:04
Here's a variation on $$\sum_{n=1}^{R} n =\frac{R(R+1)}{2}$$ I stumbled onto this a while back.
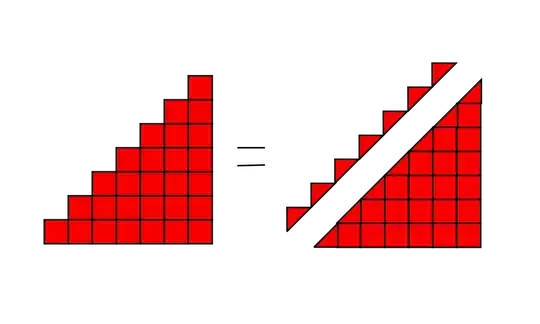
shows $$1+2+3+4+5+6+7 = \frac{1}{2}\cdot b\cdot h + \frac{1}{2}\cdot b$$ $$1+2+3+4+5+6+7 = \frac{1}{2}\cdot 7\cdot 7 + \frac{1}{2}\cdot 7$$ then $$1+2+3+4+5+6+7 = \frac{1}{2}\left( 7\cdot 7 + 7\right)$$ thus $$1+2+3+4+5+6+7 = \frac{7(7+1)}{2}$$
- 2,029
It might be too short, but my favourite mathematical proof of a not-too-mathematical concept is the ancient Chinese proof (actually1, not apocryphally) of Pythagoras' theorem. First you can explain what Pythagoras' theorem means. Then, you introduce this image:

Now you're ready to tell them the proof.
1. Behold!
(QED)
-
1I agree, I would even say that familiarity with at least one beautiful proof of the Pythagoras theorem should be a legal requirement to graduate from high school. – userX Jan 19 '15 at 02:36
-
I'd support the proof of the theorem with the following gif: http://i.imgur.com/W8VJp.gif – András Hummer Jan 19 '15 at 15:33
-
3@AndrásHummer It could be that it only works for that specific triangle or that the water doesn't entirely fill the square up by a few plank lenghts for all we know. It is not a proof by any means, while the above picture is. – user26486 Jan 24 '15 at 00:31
-
I prefer this diagram, originally devised by Thabit ibn Qurra around 900 AD. See here for a couple of animated versions. – PM 2Ring Jan 26 '15 at 10:12
-
Every rational number has a repeating decimal.
Basically, once you know how to do long division to generate digits, all you need is a very naive pigeonhole principle.
When doing the long division for $\frac{p}{q}$, the remainder is always in $0,1,\dots,q-1$. And thus, you must eventually get the same remainder to the right of the decimal, at which point, the digits start to repeat.
This is a sentimental favorite of mine. I came up with this proof in the sixth grade, when our teacher taught us that $\pi$ didn't repeat and was exactly $\frac{22}{7}$. I recall explaining the proof to a friend in the schoolyard. It was my first proof.
(One point would have to be clarified - that a "terminating" decimal is a repeating decimal with the "0" repeating...)
- 177,126
-
So, what did your teacher say when s/he saw your proof that his/her assertion was a contradiction? – Selene Routley Jan 19 '15 at 05:22
-
4@WetSavannaAnimalakaRodVance I actually never showed her the proof. I argued with her for a long time, because I did the division for $\frac{22}7$ and saw it repeated, and argued with her a bit, possibly creating a scene. :) She said, "Compute some more digits, it will stop repeating." So I gave up arguing, but came up with the general argument. – Thomas Andrews Jan 19 '15 at 05:25
-
Could we use this as a 2-for-one? Meaning first we introduce Pigeon Hole Principle, anticipating a laugh at the silly name followed by the typical 'what is that good for?' Seems to be one could explain both the PHP and this classic result in a very reasonable amount of time. As a bonus, prove $\pi \neq \frac{22}{7}$, wait 3-for-one! very nice! – userX Jan 19 '15 at 16:56
-
Well, we didn't "prove" $\pi\neq \frac{22}7$, we just proved that if $\pi$ does not repeat, then $\pi\neq \frac{22}7$ :) @userX – Thomas Andrews Jan 19 '15 at 18:40
-
Can you expand upon this? I don't see why the digits should start to repeat the moment you get the same remainder. Forgive me for asking such an elementary question. – dalastboss Jan 19 '15 at 19:47
-
Because the remainder is all information you have at each step of the division, regardless of the past steps. If you have a certain remainder, all future steps are uniquely determined. – Jasper Jan 23 '15 at 11:31
-
@ThomasAndrews: How do people like that become mathematics teachers? FWIW, I had a teacher in 6th grade who claimed that π didn't repeat and was exactly 22/7. And that guy was a prominent author of junior school arithmetic textbooks! I'd recently read an encyclopedia article on π, so I knew he was wrong. Also, our teacher in the 5th grade had introduced us to the cyclic properties of 142857. I eventually showed the 6th grade teacher the encyclopedia article after class one day, but he never recanted his original statement to the class. :( – PM 2Ring Jan 26 '15 at 10:06
Let me make it clear that I don't count this example as a proof, but I'm assuming you're using proof as a synonym of plausibility argument.
The Principle of Mathematical Induction: Let $P$ be a property about natural numbers which is true of $1$ and whenever it is true of a number, it is true of its successor. Then all natural numbers satisfy $P$.
Proof: It's true for $1$, therefore, by hypothesis, it's true for $2$. Therefore, applying the hypothesis to $2$, it is true for $3$. Therefore, applying the hypothesis to $3$, it is true for $4$. And so on and so forth.
Accompanying this presentation, I'd make a parallel between the principle of mathematical induction with its proof and an infinite row of sufficiently close domino tiles, analyzing the cases where the first one falls and where the first one doesn't fall.
- 31,356
-
-
2I like the dominoes picture. The picture I first learned was similar: "Suppose you're climbing a ladder. If you know you can reach the first rung, and you know that if you can reach any rung then you can reach the next one up, then in fact you can climb the whole ladder." – Jesse Madnick Jan 18 '15 at 03:20
I like the proof of the handshaking lemma in graph theory. I've taught it to a few students from ages 12-18 and they all seem to understand.
Lemma: There is an even number of vertices in a (finite) graph of odd degree.
The proof revolves around the fact that odd$\times$odd$=$odd, and even$+$odd$=$odd and similar facts like that.
It involves another simple lemma as well, even easier than the handshaking lemma.
Lemma 2: $\sum_v $deg$(v)=2*$the number of edges.
I like these proofs because it takes five minutes to show some legit pure mathematics to any one. Quick consequences of this are Eulers formula $V-E+R=2$ and Euler circuits etc.
- 1,325
-
Thank you Jack, I like this one too. I also vaguely remember a variation of this problem. I think the question is roughly "if 15 people work in an office, is it possible that each gets along with exactly 5 other people?" using your Lemma 2 and counting degrees of vertices leads to a simple and clean proof concluding 'not possible'. – userX Jan 19 '15 at 06:07
-
-
-
1On a similar vein, I've found the proof that any graph has at least two vertices of the same degree to be an easily accessible proof. One of the nicest bits about it is that the proof calls on the pigeonhole principle, which, if you confine your discussion to finite graphs, does a great job of illustrating the difference between common sense and a formal proof. – sju Jan 25 '15 at 16:41
For an audience with a bit of geometrical intuition about the sphere (earth), and with a markable sphere at hand to draw on, I like the proof that on a sphere, the area $\Delta$ of a spherical triangle that has angles $A$, $B$, and $C$ has area $\dfrac{(A+B+C-180°)}{720°}\odot$, where $\odot$ is the area of the sphere. (The audience doesn’t even need to know that the area of a sphere with radius $r$ is $4\pi r^2$).
First, the audience must understand that the sides of a spherical triangle must be shortest paths between the vertices, which are arcs of great circles. Some string and an appeal to airplane flights can make this point.
Then one draws the complete great circle containing each side of the triangle. These three circumferences divide the sphere’s surface into three “double lunes,” which are like the peel of an orange slice together with its antipodal peel. Each double lune contains the original spherical triangle, and each also contains the antipodal triangle. Elsewhere, the double lunes don’t overlap, and together, they cover the entire sphere.
Therefore the total area of the double lunes equals the area of the sphere plus four times the area of the triangle, which is the excess coverage beyond just covering the sphere once. They covered the triangle and antipodal triangle three times each, whereas only two of the six covers are needed to complete the coverage of the entire sphere.
The double lune with corners at $A$ and $A$’s antipode covers $\dfrac{2A}{360°}$ of the sphere, so $\frac{(2A+2B+2C)}{360°}\odot=\frac{(A+B+C)}{180°}\odot$ exceeds the sphere by four times the triangle’s area. Four times the triangle’s area is then $\frac{(A+B+C)}{180°}\odot-\odot=\frac{(A+B+C-180°)}{180°}\odot$, and the area of the triangle is $\frac{(A+B+C-180°)}{4\cdot180°}\odot$.
Thus the area $\Delta$ equals $\dfrac{A+B+C-180°}{720°}\odot$.
- 14,881
-
2I found the 'markable sphere at hand to draw on' very important. With your explanation and the diagrams here http://web.cortland.edu/jubrani/375ch5.pdf I was able to follow it. I think this is excellent. Once understood, I think the general audience would feel like they learned something non-trivial, and the requirements to understand this are very minimal. I had never seen this before, thank you! – userX Jan 19 '15 at 07:11
-
I remember learning this in graduate school. I thought it was beautiful and was shocked that I’d never known about it. It’s also a nice starting point for further ideas about non-Euclidean geometry. Question: If the five angles of a regular pentagon each measure 90°, where are you? – Steve Kass Jan 19 '15 at 15:48
The Stable Marriage Theorem of Gale & Shapley. There is hardly anything in the statement or proof that even looks like mathematics to a "general audience". I haven't tried telling it to a general audience myself, but I'm sure a skilled expositor could get it across in $5+\varepsilon$ minutes, for some sufficiently large value of $\varepsilon$.
- 78,265
-
very nice, it seems to me in a classroom setting one could take this further and actually carry out the algorithm live. If one could pull this off it would be a very nice example of beautiful mathematics that may not feel like math to participants, I do agree on the +$\epsilon$ point.. might be a large epsilon :-) thank you! – userX Jan 18 '15 at 01:46
I would choose the proof that the set of reals is too big to form a sequence from it. However I'm not sure if 5min would be enough time ;)
- 698
-
14Even explaining (properly) what a real number is would take about 20 minutes at least. – Jack M Jan 17 '15 at 23:33
-
4I would not say exactly what real number is. Everyone from that audience should have some intuition and knowledge about real numbers from school and that would be enough in my opinion to understand the proof. – pw1822 Jan 17 '15 at 23:37
-
Just to be clear, Are you talking about cantors diagonalization argument ? – userX Jan 17 '15 at 23:48
-
1
-
1yes, I very much like that one there is a very nice presentation here http://youtu.be/elvOZm0d4H0 on such proof at 3:35 mark, it is very elegant. thank you for suggesting this one.. and they do it in a tone appropriate for general audiences.. very well done! – userX Jan 18 '15 at 02:03
-
That's a pretty nice presentation. I haven'n known this chanell.
I like this proof because it was one of the things thanks to which I started interesting in mathematics.
– pw1822 Jan 18 '15 at 02:15 -
Some infinity paradox like Hilberts hotel would be better ... – kjetil b halvorsen Jan 19 '15 at 19:00
-
-
Cantor’s diagonal, you mean? My favourite back-of-the-napkin proof! – Micah Walter Jan 21 '15 at 03:02
-
Could you say a little more about this proof? I am not sure if heard about it. – pw1822 Jan 21 '15 at 20:07
There's one statement with proof I really like that seems accessible to a wide audience rather quickly.
Statement: For any natural number $n$, there exist $n$ consecutive natural numbers that do not contain a prime number.
Proof: Consider the sequence $(n+1)!+2, (n+1)!+3, \ldots ,(n+1)!+(n+1)$. These numbers are divisible by $2, 3, \ldots, n+1$, respectively. In a five-minute version to a non-science Ba, one shouldn't mention the word 'factorial' (just say something like 'multiply the first ... numbers'). The main part required is that $2$ divides both $2\cdot a$ and $2$, hence $2$ divides $2+2\cdot a$, and similarly for other numbers than $2$.
If there's time left or if one has another $5\pm\epsilon$ minutes, one could explain that there are infinitely many primes (via Euclid's argument). When this seems contradictory (which might very well be the case, when one's talking to, say, a historian), it is a nice idea to talk about how large these factorials actually become.
- 2,744
-
1yes.. i like this one too.. I concur, I think this can be shared with a general audience and I think is a very nice question and very nice solution, thank you! – userX Jan 18 '15 at 02:18
-
-
Somehow, I once started getting confused if $1$ or $2$ should be used and, for some reason, got it mixed up by now. Thanks for pointing it out - I just edited accordingly. – HSN Jan 19 '15 at 15:22
-
There's nothing wrong with introducing a term like factorial if the concept is simple, which it is in this case. – Théophile Jan 19 '15 at 15:54
-
Geometric series.
\begin{align} S&=\quad\;\,1+\frac1x+\frac1{x^2}+\frac1{x^3}+\dotsb\\ Sx&=x+1+\frac1x+\frac1{x^2}+\frac1{x^3}+\dotsb\\ Sx-S&=x\\ S(x-1)&=x\\ S&=\frac{x}{x-1} \end{align}
And, if time permits, a variant:
\begin{align} S&=\quad\;\,\quad\;\,\frac1x+\frac2{x^2}+\frac3{x^3}+\dotsb\\ Sx&=\quad\;\,1+\frac2x+\frac3{x^2}+\frac4{x^3}+\dotsb\\ Sx^2&=x+2+\frac3x+\frac4{x^2}+\frac5{x^3}+\dotsb \end{align} Rearranging, then summing: \begin{align} Sx^2&=x+2+\frac3x+\frac4{x^2}+\frac5{x^3}+\dotsb&Sx&=1+\frac2x+\frac3{x^2}+\frac4{x^3}+\dotsb\\ S&=\quad\;\,\quad\;\,\frac1x+\frac2{x^2}+\frac3{x^3}+\dotsb&Sx&=1+\frac2x+\frac3{x^2}+\frac4{x^3}+\dotsb\\ \hline Sx^2+S&=x+2+\frac4x+\frac6{x^2}+\frac8{x^3}+\dotsb&2Sx&=2+\frac4x+\frac6{x^2}+\frac8{x^3}+\dotsb \end{align} Thus, we have: \begin{align} Sx^2+S&=x+2Sx\\ Sx^2-2Sx+S&=x\\ S(x^2-2x+1)&=x\\ S&=\frac x{x^2-2x+1} \end{align}
As I finish typing this, I realize that perhaps the variant isn't as "accessible to a general audience" as the first one.
- 11,331
- 23,062
-
1It might be easier to demonstrate the variant by multiplying the terms in $S(S-1)$ (using the $S$ from the original problem). Thus $$\frac1x+\frac2{x^2}+\frac3{x^3}+\dotsb = \big(1+\frac1x+\frac1{x^2}+\dotsb \big)\big(\frac1x+\frac1{x^2}+\frac1{x^3}+\dotsb \big) = \big(\frac{x}{x-1}\big) \big(\frac{x}{x-1} - 1\big) = \frac{x}{(x-1)^2}.$$ – Théophile Jan 19 '15 at 05:21
-
2Is there a reason you use $\frac{1}{x}$ for the common ration, rather than $x$? It makes it so much harder to read. – Thomas Andrews Jan 19 '15 at 14:25
-
1
A group of people stranded on a desert island (that aren't all the same sex) can produce at most a number of generations equal to one less than the population size while avoiding incest.
Proof: Take any descendent of the initial population, call them Alice.
Then one of Alice's parents is of the previous generation to Alice herself (i.e. if Alice is of generation 5, then at least one of her parents is of generation 4).
Also, Alice has more ancestors than that parent (since Alice's ancestors are the ancestors of both of her parents, who can't have any ancestors in common since we're not allowing incest).
So now let's climb up the genealogical tree to this parent of Alice's. In so doing the number of ancestors in the initial population "above us" goes down by at least one, and the generation goes down by exactly one.
Keep doing this until you climb back up to the initial population. You'll make a number of jumps equal to Alice's generation (if we call people in the initial population generation zero), and at each jump the number of ancestors goes down by at least one. Since we're now back up at the initial population, we have 1 ancestor (ourselves). So we lowered the number of ancestors a number of times equal to Alice's generation, and ended up with 1. So, Alice's generation can't be any more than one less than the number of ancestors she has (if she has 6 ancestors, she can't be of generation 6 or more because then we would have subtracted something from 6 six times and ended up with 1). Now, in the best case scenario Alice has everyone as an ancestor, so her generation can't possibly be more than one less than the initial population size. $\blacksquare$
Depending on how badly algebra class has mentally scarred your friend, you may find it easier to use names for the various numbers - $n$ and $G$ and whatnot. I was trying to avoid that because some people really do start to get nervous as soon as they hear you say "Let $x$...".
Be sure to illustrate with a drawing of an example genealogical tree as you explain. Even I'm not sure I'd be able to follow the above if the explanation was purely verbal.
- 27,819
- 7
- 63
- 129
-
You can probably give a much better bound than $n-1$. Somewhere in the vicinity of $\log_2 n$. – Asaf Karagila Jan 18 '15 at 00:04
-
@AsafKaragila You can't - in fact, there is a fairly simple algorithm for creating someone of generation $n-1$ given a mixed-sex population of size $n$. – Jack M Jan 18 '15 at 00:13
-
3
-
2How do you assign a "generation" to an individual? How is "incest" defined here? Is having offspring with one's seventh cousin twice removed "incest" here? Since that term is non-constant among cultures it needs a definition. – Jeppe Stig Nielsen Jan 18 '15 at 00:28
-
1Incest means sex with someone with whom you have a common ancestor in the initial population. Generation is zero for the initial population, and otherwise is one more than the maximum of your parents' generations. – Jack M Jan 18 '15 at 01:45
-
Very nice! I agree this is an excellent example, but a well crafted visual diagram would be essential for maximum accessibility, like a powerpoint presentation. The definition of incest is crucial, as stated in your comments. Still this one is new to me, it's a good candidate, and I appreciate it, thank you. @JackM – userX Jan 18 '15 at 03:09
-
2
-
You can rework this into an estimate of the amount of time since any two people in the world have shared a common ancestor. Not a great estimate since incest (your definition, not the legal definition) makes it impossible to say for sure, but I think that's much more likely to appeal to lots of people who don't consider themselves mathematically inclined. – David Z Jan 23 '15 at 10:13
In high school one learns that $\left(-a\right)\left(-b\right)=ab$, but in my experience the proof is never given, or a clear reason. The proof is easy using the number systems that people in America are comfortable with, i.e $\mathbb{R}$, and of course the notion that $a\left(0\right)=0$.
Proof: $\left(-a\right)\left(0\right)=0$
$\implies \left(-a\right)\left(b+\left(-b\right)\right)=0$
$\implies\left(-a\right)\left(b\right)+\left(-a\right)\left(-b\right)=0$
$\implies \left(a\right)\left(b\right)+ \left(-a\right)\left(b\right)+\left(-a\right)\left(-b\right)=\left(a\right)\left(b\right)$
$\implies 0+\left(-a\right)\left(-b\right)=\left(a\right)\left(b\right)$
$\therefore \left(-a\right)\left(-b\right)=\left(a\right)\left(b\right)$
- 577
-
9Accessible, perhaps, but I think it's a challenge for a general audience to appreciate. They could easily be confused about why we need a bunch of formal rules just to prove another formal rule. – Erick Wong Jan 19 '15 at 03:11
-
2I agree with Krampus that this should be much better-known, but I also agree with Erick that it might not fit the topic of this question. (I cover this topic when I teach future mathematics teachers; I think every teacher of mathematics should be able to demonstrate why “negative times negative is positive” as rigorously as this, if asked to, say by a curious student, but I’m not sure the proof needs to be taught in the elementary or high school curriculum.) – Steve Kass Jan 19 '15 at 04:29
-
1I've actually been teaching basic algebra this way for more than a decade, except we learn the names of the field axioms and every step needs to be justified by such, or a theorem or a definition. So the above is nearly identical to what I have been doing in class, except we would include the justifications on each step such as commutativity, associativity, cancellation law of addition, distributive law etc. Seems ridiculous to me that students go thru 12+ years of math and never take a week or two to learn what they can and can't do [field axioms]. – userX Jan 19 '15 at 06:23
Problem: A red ribbon is tied tightly around the earth at the equator (assume the earth is a perfect sphere). How much more ribbon would you need if you raised the ribbon 1 ft above the equator everywhere?
Answer: Only a tad bit more than 6 ft!
Solution: Let $r$ be the radius of the earth in feet. Then the circumference (length of the ribbon) is $2\pi r$. When we increase the radius by $1$ foot, the new radius is $r+1$, so the new circumference is $2\pi(r+1)$. Thus, you need $$ 2\pi(r+1)-2\pi r = 2\pi \approx 6.28 $$ extra feet of ribbon.
I think this is a very non-intuitive answer (and one you can certainly explain in a very brief time). Firstly, you are not given the radius of the earth at the beginning, and that seems a bit weird. Secondly, only $6.28$ feet!? That seems quite bizarre that you could raise the ribbon by $1$ foot everywhere around such a huge object as a planet and only need a little more than $6$ feet of ribbon to do it.
If you have more time on your hands, then you could even discuss the many generalizations of this kind of argument where you are not dealing with circular objects. For example, see Ravi Vakil's paper The Mathematics of Doodling in the American Mathematical Monthly.
- 22,531
The empty set is contained in any other set. Suppose there exists a set $A$ such that $\varnothing \not\subset A$. Then exists $x \in \varnothing$ such that $x \not\in A$. Oh, wait!
- 77,665
-
36Is this really such a great example? I mean, for one thing I don't see why the statement "for all sets $A$, $\varnothing \subset A$" would be of any interest whatsoever to the average adult -- it's barely of interest to me! Besides which, no one will actually get anything out of this unless they first understand (1) "what is a set?", (2) "when is one set contained in another?" (precisely), and (3) "what is the empty set?" (and why would we bother defining such an object at all?). I don't thing someone can be exposed to these ideas in 5 minutes, except very superficially. – Mike F Jan 18 '15 at 00:55
-
If it is such a great example I do not know, but people seem to like it. If the statement is to be explained (even superficially) to a general audience, I think it is safe to assume (unless it was a classroom full of children who don't give a crap to what you're saying) that the people there do have a minimum interest on whatever it is going to be said. And these ideas should be passed superficially, yes, the point would be to catch the interest of the audience with this type of argument. Technical details would only bore them at this point. – Ivo Terek Jan 18 '15 at 01:03
-
1@MikeF I agree, "for all sets $A$, $\varnothing \subset A$" seems like a hard sell to a general audience, yet I find the proof so short and elegant and potent... thats why I enjoyed it.. your point is valid, how much of this can we share with a general audience in 5 minutes.. the trouble with doing this superficially is that i don't think they would enjoy it as much.. – userX Jan 18 '15 at 02:13
-
7Strictly speaking, $\varnothing \subset A$ does not hold for $A = \varnothing$. You probably meant $\varnothing \subseteq A$. – wchargin Jan 18 '15 at 04:21
-
18@WChargin: Plenty of people use "$\subset$" the way that you use "$\subseteq$", and use notation like "$\subsetneq$" or similar when strict containment is meant. – Mike F Jan 18 '15 at 05:49
-
1"The empty set is contained in any other set" or "Nothing(ness) is everywhere". – Unit Jan 19 '15 at 02:34
-
1@Unit: That is the best nihilistic interpretation of set theory I have ever heard. Kudos! – Asaf Karagila Jan 19 '15 at 15:55
-
It took me a while to get this, and it was staring me right in the face.
"If nothing isn't in A, there's something in nothing that isn't in A, but that means that there's something in nothing, but nothing's in nothing."
– Axoren Jan 19 '15 at 18:32 -
4
-
Took me a while to decipher. This should have read "The empty set is a subset of any set $A$ because all its members are in $A$." Yeah... shocking. -1 for writing it in a convoluted way so that it somehow may seem surprising. – user2345215 Jan 22 '15 at 00:28
I would explain the Pigeon Hole principle, or one of its many guises.
In fact, I remember explaining the PHP to a non math student while playing bridge.
I told him that one gets at least $4$ cards of some suit- which is really the PHP.
You can come up with many other interesting "real life" examples, and it's fun.
- 13,182
-
4A bridge squeeze, I suppose, is a sort of pigeonhole principle... – Thomas Andrews Jan 19 '15 at 18:42
How about the proof that if $p=2^{n}-1$ is prime, then $k=(2^{n}-1)\cdot 2^{n-1}$ is a perfect number?
[The factors of $k$ are $1, 2,4,\cdots,2^{n-1}, p, 2p, 4p,\cdots, 2^{n-1}p$ .]
- 40,402
One of my favorite proofs given constraints such as these is:
Theorem. $n^2 - n$ is even for all natural numbers $n$.
The proof can be carried out in many different ways depending on your "general" audience.
I have written up a sketch of the entire talk on MO and re-mentioned it on MESE.
See also the couple of different generalizations around the identity $(n-1)n = n^2 - n$.
- 14,451
-
1So many approaches to this, very nice! This showcases, to some extent, the role creativity plays in math and in problem solving in general. I think it's excellent. Thank you! by the way, did you actually give this talk? and if so, how did it go? was the audience of general background? – userX Jan 19 '15 at 19:18
-
@userX Yes, I have given this talk to pre-service and in-service secondary school teachers (who were graduate students at Teachers College Columbia University). I gave it as a "model" lecture for students attending a teaching seminar; I think it went pretty well, since the attendees looked to be quite engaged (and I was invited back to give another talk the next year - that one ended up being about the multiplication table). – Benjamin Dickman Jan 19 '15 at 19:41
-
1very nice! This sort of creativity party is what I enjoy most. Thank you! – userX Jan 19 '15 at 19:51
I really like proofs using the pigeonhole principle I give two examples I think most people should know should know.
Example 1:
In a party with $n$ persons there are always two persons who have shaken hands with the same number of people. Proof: clearly in parties people don't shake hands with the same person twice (for sufficiently low alcohol levels). Intitially a person can shake hands any number of times from $0$ to $n-1$ ($n$ possible values). But notice if someone shook $0$ times then no one shook $n-1$ times, hence there are at most $n-1$ possible distinct values for the number of hands each person shook.
Since there are $n-1$ values and $n$ persons at least two must have shook the same amount of hands
Example 2:
In a party of $6$ or more there is a group of three persons who all know each other or a group of three persons such that none of them know each other.
Proof: Choose a random person, call him Bob. Then the remaining people (who number at least $5$) can be classified into two groups: those that know Bob and those that don't. The largest of these groups has at least three persons. Suppose the group of people who do know Bob is larger than $3$ (the other case is analogous). Now suppose there are two persons in that group that know each other. Pick Bob and those two persons and you have a group of three which all know each other. So the statement is true, the other case is when none of the people in the group know each other, pick three of the people in the group and then those three people don't know each other. So the statement is again true.
-
That seems to be a really good mix of clever and relatable to regular people. I like it. – Fred Hamilton Jan 25 '15 at 23:21
Taking $\epsilon = 5$ minutes here, we presented a lecture to psychologists, engineers, philosophers and also mathematicians over Game Theory, and how to take better decisions with examples, and different problems.
So we took about $10$ minutes to explain Nash Equilibrium to them, using the most famous Prisoner's Dilemma.
I believe everyone on the lecture understood the concept and went out of there knowing what this important idea has to do with economy, games and also mathematics.
- 17,571
While possibly a bit silly, I find that the (utterly trivial) proof of the uniqueness of identity elements very nicely illustrates how "abstract" mathematical proofs "work" and how, at least not totally trivial, questions can get very simple answers if posed correctly.
While the proof itself obviously does not require 5 minutes to present one would probably have to use a few minutes to introduce the concept of an identity element (and why its of any interest) and possibly give some comments on what one means by mathematical "structure" more generally.
- 1,051
I love the proof that a finite group of even order has an element that is its own inverse. I realize that groups are not nearly as well understood as they should be to a general audience, but that is the fault of our education priorities, as groups are everywhere in math and nature.
Anyway, the proof. Let $G$ be a group of finite even order. We want to show there is an element $h\in G$ such that $h\ne e$ and $h^2=e$, where $e$ is the group identity. We pick an element $g\in G$. If $g^2\ne e$, then we remove the elements $g, g^{-1}$, which must be unique. Removing 2 elements from an even set leaves an even set. We can continue to remove pairs of elements and their inverses until we find an element which is its own inverse (and we are done), or else we finally get to the last 2 elements of our group (the smallest even set), which must be the identity $e$ and some other element $h$ (since our procedure will never remove $e$). These two elements must include the inverse of $h$ by the inverse property of groups, and since $e$ cannot be the inverse of $h$, $h$ must be its own inverse. QED
-
7I actually love this proof too, but I think explaining it to first semesters abstract algebra students would take a good 20-30 minutes, if they already know what a group is. I am not sure this is a 5 minute one for the general public. – userX Jan 19 '15 at 05:59
-
Yes, you are probably and unfortunately correct. We need to teach groups much earlier and connect them with the concept of symmetry, which I think would resonate with more people. – Jan 21 '15 at 00:54
Proof that $\sqrt 2$ is irrational: Any non-integer fraction multiplied by itself cannot be an integer.
(So a full length proof along these lines would first have to show that the prime factorization of integers is unique, and this turns out to be rather hard. But any young kid who has learned about prime factorization will accept this without proof.)
- 26,430
- 2
- 35
- 64
There's no way to tune a piano in perfect harmony.
There are twelve half-steps in the chromatic scale, twelve notes in each octave of the keyboard. Start at middle "C", and ascend a perfect fifth to "G". That's seven half steps up, with a frequency ratio of 3/2. Drop an octave to the lower "g" -- that's twelve half steps down, and a frequency ratio of 1/2. Continuing around the "circle of fifths" twelve times, and dropping an octave seven times, brings you back to middle "C", a frequency ratio of 1.
So, $1 = (\frac{3}{2})^{12} \times (\frac{1}{2})^7$, or $3^{12}=2^{19}$.
Ask your piano tuner next time about those fifths.
- 181
-
4For a non-musician the term "perfect harmony" might need to be explained (or defined) first. – Paŭlo Ebermann Jan 24 '15 at 09:34
-
The term is used here to be more suggestive than precise. A more precise statement might be, "There's no way to tune a piano to just intonation simultaneously in all keys." – Steve Mitchell Jan 27 '15 at 20:10
A proof that needs five seconds rather than five minutes, but I find instructive nonetheless: Suppose you have a line in $\mathbb{R}^2$ together with two points $A$ and $B$ on the same side of the line. Determine the point where the distance travelled by an object moving from A to B being reflected at the line is minimal.
Too lazy to draw up a diagram. Show people the problem, then reflect one of the points on the line and they will suddenly see...
A great example to show the beauty of mathematics without involving anything abstract or scary numbers. Also a good opportunity to explain some basics.
- 274
One of the first proofs I was shown was in a discrete structures class. I don't think this would survive the rigors of formal proof, but I really enjoyed it.
Definitions:
$N$ is the set of numbers starting with 0, 1, 2, $\dots $
A number in our set $N$ is odd if and only if there exists another number in our set $N$ that when multiplied by two and added to one yields the number in question. Or more formally
$\forall a \in N$, a is odd if $\exists b \in N \ni a = 2b + 1$
To Prove:
If $n$ is odd then $n^2$ is odd
Proof: Direct
Let us assume that we take an "odd" number, $n$. Then "n is odd" is true. Let us prove that $n^2$ is true.
By our assumptions $n$ is odd
This is the critical part of the proof, that might need some convincing
Since $n$ is odd we can use the definition of an odd number above and state that, $ \exists x \in N \ni n=2x+1$.
Now we can substitute our number $n$ with $2x+1$ and state $n=2x+1$
Further to prove $n^2$ is odd, we need only show that $(2x+1)^2$ is odd
This also might need some examples to convince
By distributive property, $(2x+1)^2=4x^2+4x+1$
Now we can refactor and rewrite $4x^2+4x+1=2(2x^2+2x)+1$
We know from rules of arithimetic that $2x^2+2x$ is a number which we can call $z$ and $z=2x^2+2x$
By substitution $2(2x^2+2x)+1=$2z+1$
$\therefore$ by definition of odd number $2(2x^2+2x)+1$ is odd
- 265