5

Given 1 continuous function $f(x)$ defined on a 1-dimensional interval $[-1,1]$, the IVT says that if:

  • $f(-1)<0$ and
  • $f(1)>0$

then there is an $x$ such that $f(x)=0$.

I am trying to prove the following extension:

Given 2 continuous functions $f(x,y)$ and $g(x,y)$ defined on a 2-dimensional square $[-1,1]\times[-1,1]$, if:

  • for all $y$: $f(-1,y)<0$ and $f(1,y)>0$
  • for all $x$: $g(x,-1)<0$ and $g(x,1)>0$

then there are $x,y$ such that $f(x,y)=g(x,y)=0$.

My current "proof" is graphic:

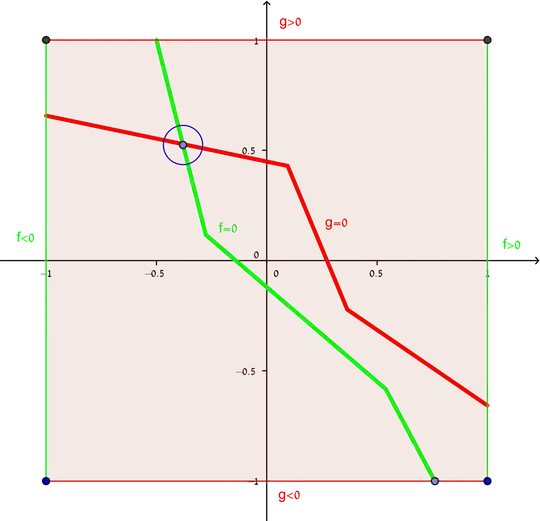
enter image description here

I.e., by the condition on $f$ (green), there must be a connected "wall" (green), separating the west side from the east side, in which $f=0$. Otherwise we could go from $f<0$ to $f>0$ without passing through $f=0$, which is impossible.

Similarly, by the condition on $g$ (red), there must be a connected "wall" separating the north side from the south side, in which $g=0$.

These walls must have an intersection point in which both functions are 0.

MY QUESTIONS ARE:

  • Is this idea correct?
  • If it is correct, how can it be formalized?
  • Are there generalizations of this theorem to many dimensions?
Erel Segal-Halevi
  • 10,555
  • I just found a MathImages article which uses pretty much the same graphic intuition to explain Brouwer's fixed-point theorem in two dimensions: http://mathforum.org/mathimages/index.php/Brouwer_Fixed_Point_Theorem – Erel Segal-Halevi Dec 19 '14 at 06:19

3 Answers3

5

In fact, this is the Poincaré–Miranda theorem. It holds in arbitrary dimensions: Given $n$ continuous functions $f_1\dots f_n$ on $[-1,1]^n$ with $f_i$ being positive on the face with $x_i=-1$ and negative on $x_i=1$. Then there is a point in the cube, where all these functions simultaneously vanish.

daw
  • 49,113
  • 2
  • 38
  • 76
3

It is true but non-trivial and your idea cannot be formalized because the set of points at which $f$ is zero do not at all have to look like what you drew. They could for example be some weird set that looks like blotches, which may even be disconnected or fractal or both.

To prove it, use the 2d Intermediate value theorem, where $f,g$ are the two components of the continuous function from the square to $\mathbb{R}^2$. It is easy to check that that function on the square's boundary winds around $(0,0)$ and hence we are done.

Community
  • 1
user21820
  • 57,693
  • 9
  • 98
  • 256
  • Unanswered part: I am certain the analogous theorem holds for higher dimensions, but have no idea how to prove it. The 2d intermediate value theorem using the winding number does not seem to have a nice generalization. – user21820 Dec 18 '14 at 14:39
  • I think using the winding number does generalize: https://en.wikipedia.org/wiki/Degree_of_a_continuous_mapping – mr_e_man Jan 11 '23 at 21:32
  • @mr_e_man: I know that degree is the high-order generalization of winding number. But my comment was that there seems to be no nice generalization of the proof using the winding number. If you know one, can you sketch it? – user21820 Jan 12 '23 at 02:38
  • It's in the middle of the answer you linked. It looks like it generalizes directly to 3D and higher dimensions. But I'm not very familiar with this topic; I can't guarantee that it actually works. – mr_e_man Jan 12 '23 at 03:59
  • @mr_e_man: Are you referring to the "Sketch of Proof of IVT in Two Dimensions"? That works easily for 2d, because there is a simple elementary definition of winding number for 2d, and with this definition is it obvious that the winding number of the function on the square's boundary is 1. I'm not familiar with this topic, but it seems to me there is no such simple definition beyond 2d. By the way, note that my "unanswered" comment was half a year before daw posted that this question is just Poincare-Miranda, so it's been answered. =) – user21820 Jan 12 '23 at 04:10
  • Yes, that's what I was referring to. -- There are two generalizations of the IVT; the one in Jim Belk's answer is stronger than the one in the OP here. It wasn't clear which one you were referring to as "unanswered" (in 3D or higher). – mr_e_man Jan 12 '23 at 19:47
  • I can't say anything about simplicity or obviousness. Let's not continue this discussion; I really don't know what I'm talking about. – mr_e_man Jan 12 '23 at 20:00
  • https://math.stackexchange.com/questions/2708308/what-are-the-higher-dimensional-generalisation-of-intermediate-value-theorem-and – mr_e_man Nov 17 '23 at 01:36
  • @mr_e_man: Anything that uses "degree" is going to be not as simple as the simple definition of winding number for 2d that I linked you to. Moreover, unsurprisingly, the post you linked to says "I claim without proof", as is common for 'explanations' that invoke "degree". – user21820 Nov 17 '23 at 14:16
3

Based on an answer by Itai Weiss, I think I can prove the claim.

Suppose by contradiction that the claim is false, i.e. there is no point in $[-1,1]\times[-1,1]$ on which $f=g=0$. We show a continuous function $h(x,y)$ from $[-1,1]\times[-1,1]$ to $[-1,1]\times[-1,1]$ which does NOT have a fixed point, contradicting the Brouwer fixed-point theorem.

Define:

$$h = \frac{-(f,g)}{\max(|f|,|g|)}$$

Because of the assumption, the denominator is always positive, so $h$ is defined and continuous in all of $[-1,1]\times[-1,1]$.

$h$ maps every point in $[-1,1]\times[-1,1]$ to the boundary of $[-1,1]\times[-1,1]$, in particular:

  • If $|f|\geq|g|$ then $|h_x|=1$ so $h$ is on the left boundary (if $f>0$) or the right boundary (if $f<0$);
  • If $|g|\geq|f|$ then $|h_y|=1$ so $h$ is on the bottom boundary (if $g>0$) or the top boundary (if $g<0$).

In particular, this means that $h$ has no fixed point in its interior. We now prove that it has no fixed point in its boundary:

  • On the left boundary $f<0$, so $h$ goes either to the right boundary (if $|f|\geq|g|$) or to the interior of the top/bottom boundaries (if $|f|<|g|$); in any cas $h$ is not on the left boundary.
  • The same is true in the other 3 cases.

Hence, $h$ has no fixed point - a contradiction.

Comments are welcome!

Community
  • 1
Erel Segal-Halevi
  • 10,555